Veelhoeksgetal
Een veelhoeksgetal is een getal dat het aantal bolletjes is van een figuur met in een hoekpunt geneste regelmatige veelhoeken. In de oudheid ontdekte men dat getallen waren weer te geven door een aantal figuurtjes zoals rijstkorrels of zaden te rangschikken in een figuur, dit noemt men figuratieve getallen. De veelhoeksgetallen zijn daar een voorbeeld van. De bekendste soorten veelhoeksgetallen zijn de driehoeksgetallen en kwadraatgetallen.
De gelijkvormige veelhoeken, steeds met een zijde één groter, die een veelhoeksgetal samenstellen, hebben één gezamenlijk hoekpunt. Alle veelhoeken hierin met zijden van minimaal één delen bovendien voor een deel de beide zijden, die aan dit hoekpunt liggen.
Voor veelhoeksgetallen geldt de veelhoeksgetalstelling van Fermat, die zegt dat ieder positief geheel getal de som is van ten hoogste -hoeksgetallen.
Het -de -hoeksgetal verkrijgt men door het bijplaatsen van zijden met voor elke zijde bolletjes en het verlengen van één zijde van de vorige figuur met één bolletje. Dat leidt tot de recurrente betrekking:
Voor een groter aantal hoeken moet men bedenken dat de veelhoeken één gezamenlijk hoekpunt hebben en dat vanuit dat hoekpunt de zijden in dezelfde richting samenvallen.
De volgende figuur is een voorbeeld van zeshoeksgetallen:
| 1 | 6 | 15 | 28 | |||
|---|---|---|---|---|---|---|
Als het aantal zijden is van een veelhoek, dan is de formule voor het e -hoeksgetal gegeven door
Elk veelhoeksgetal is ook uit te drukken in de driehoeksgetallen , namelijk
Een tabel met de eerste veelhoeksgetallen is:
| Naam | Formule | n | OEIS | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||
| driehoeksgetal | 1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 | rij A000217 in OEIS | |
| kwadraatgetal | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | rij A000290 in OEIS | |
| vijfhoeksgetal | 1 | 5 | 12 | 22 | 35 | 51 | 70 | 92 | rij A000326 in OEIS | |
| zeshoeksgetal | 1 | 6 | 15 | 28 | 45 | 66 | 91 | 120 | rij A000384 in OEIS | |
| heptagonaal getal | 1 | 7 | 18 | 34 | 55 | 81 | 112 | 148 | rij A000566 in OEIS | |
| achthoeksgetal | 1 | 8 | 21 | 40 | 65 | 96 | 133 | 176 | rij A000567 in OEIS | |
| negenhoeksgetal | 1 | 9 | 24 | 46 | 75 | 111 | 154 | 204 | rij A001106 in OEIS | |
| 10-hoeksgetal | 1 | 10 | 27 | 52 | 85 | 126 | 175 | 232 | rij A001107 in OEIS | |
| 11-hoeksgetal | 1 | 11 | 30 | 58 | 95 | 141 | 196 | 260 | rij A051682 in OEIS | |
| 12-hoeksgetal | 1 | 12 | 33 | 64 | 105 | 156 | 217 | 288 | rij A051624 in OEIS | |
Gecentreerde veelhoeksgetallen[bewerken | brontekst bewerken]
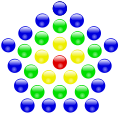
Er is een verschil tussen de veelhoeksgetallen gedefinieerd vanuit een hoekpunt en gecentreerde veelhoeksgetallen. Veelhoeksgetallen met in een hoekpunt geneste veelhoeken en gecentreerde veelhoeksgetallen voor dezelfde veelhoek zijn niet hetzelfde. Als het aantal zijden is van een veelhoek, dan is de formule voor het gecentreerde e -hoeksgetal anders dan voor het gewone e -hoeksgetal.
De verschillende veelhoeken, die een gecentreerd veelhoeksgetal samenstellen, hebben geen punten hetzelfde.
-
22 is het vierde vijfhoeksgetal.
-
31 is het vierde gecentreerde vijfhoeksgetal.
Websites[bewerken | brontekst bewerken]
- rij A086270 in OEIS. veelhoeksgetallen
- (en) MathWorld. Polygonal Number.