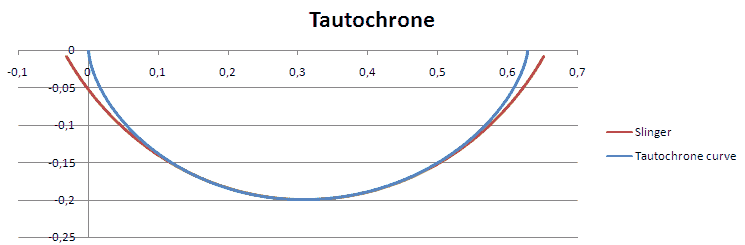
Tautochrone kromme

Een tautochrone of isochrone kromme (Grieks: τὸ αὐτό, dezelfde, ισος, gelijk en χρονος, tijd) is een kromme waarvoor geldt dat het voor de tijd die een voorwerp er over doet om er langs naar beneden te glijden niet uitmaakt of het deeltje hoger of lager los gelaten wordt. Het voorwerp is een wrijvingsloos puntdeeltje, en er is een gelijkmatig uniform gravitatieveld. Als het deeltje hoger los gelaten wordt beweegt het sneller, waardoor het in dezelfde tijd beneden komt. De perfecte tautochrone kromme blijkt een cycloïde vorm te hebben.
Slinger[bewerken | brontekst bewerken]
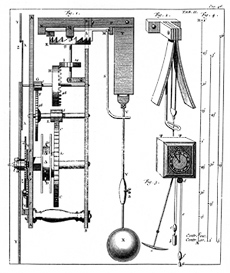
Als men erin slaagt een deeltje langs een tautochrone kromme te laten slingeren, heeft men een slinger met een slingertijd die onafhankelijk is van de uitwijking. Zo ontstond het "tautochrone probleem", de wiskundige puzzel om de juiste curve te vinden. Dit probleem werd opgelost door Christiaan Huygens in 1659. Hij bewees in zijn werk Horologium oscillatorium (1673) dat deze kromme een cycloïde moest zijn. Hij liet bovendien zien dat men een slinger - die uit zichzelf natuurlijk een deel van een cirkelbaan beschrijft - zo'n cycloïdebeweging kan laten maken door links en rechts van het bevestigingspunt van de slinger twee "wangen" te bevestigen die ook zelf de vorm van een cycloïde moeten hebben.
De slingertijd T van het deeltje is gelijk aan:
- .
Daarin is r de straal van de "afrollende" cirkel die de cycloïde produceert en g de valversnelling.
Bewijs dat de tautochrone kromme een cycloïde is[bewerken | brontekst bewerken]
Het onderstaande bewijs volgt de lijnen waarlangs Abel een algemener probleem aanpakte.
We veronderstellen het onderste punt in y = 0 en noemen h de hoogte vanwaar het voorwerp begint. De kinetische energie op een hoogte y is juist de verloren potentiële energie. Als we met s de afstand tot het punt y = 0 langs de kromme aanduiden, is dus:
- .
Daaruit volgt:
Na integratie vinden we de tijd T(h) die het voorwerp nodig heeft om van de hoogte h het onderste punt te bereiken.
De laatste gelijkheid geeft T (op een constante na) als de convolutie van en . Met behulp van Laplace-transformatie volgt:
Nu is voor de tautochrone kromme T constant, en de Laplace-getransformeerden zijn: en , zodat:
- .
Met behulp van de bovengenoemde getransformeerde zien we door terugtransformatie:
- .
Omdat
volgt:
of na enig gereken:
Dit is een differentiaalvergelijking voor een cycloïde.
Brachistochrone kromme[bewerken | brontekst bewerken]
De oplossing van het "tautochrone probleem" werd later door Jakob Bernoulli gebruikt om ook het probleem van de brachistochrone kromme op te lossen (Acta Eruditorum, 1690); daarin gebruikte hij voor het eerst de term integraal.









![{\displaystyle {\sqrt {2g}}{\mathcal {L}}[T]={\mathcal {L}}\left[{\frac {1}{\sqrt {y}}}\right]{\mathcal {L}}\left[{\frac {ds}{dy}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a8ef6ceb32c69b4461d34b2079217697a820991)
![{\displaystyle {\mathcal {L}}\left[{\frac {1}{\sqrt {y}}}\right]={\sqrt {\frac {\pi }{z}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e684c32a1476831bf0770d3490f45be5c9cf7a1)
![{\displaystyle {\mathcal {L}}\left[1\right]={\frac {1}{z}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50b56b031a3438e7fec93253997af3106bb26c94)
![{\displaystyle {\mathcal {L}}\left[{\frac {ds}{dy}}\right]=kz^{-{\frac {1}{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4563fd03ed2f6b805968c08934f8ddb8b50b16ba)