Elektronische bandstructuur
In vastestoffysica beschrijft de elektronische bandstructuur (of simpelweg de bandstructuur) van een vaste stof het spectrum aan energieën waarin een elektron zich wel (genaamd energieband) of niet (genaamd verboden zones, band gap's of energiekloven) kan bevinden. Bandtheorie leidt deze banden en bandkloven af door de toegestane kwantummechanische golffunctie's van een elektron in grote periodieke roosters van atomen of moleculen te onderzoeken. Bandtheorie is voor vaste stoffen erg succesvol gebleken in het verklaren van de vele fysische eigenschappen, waaronder elektrische resistiviteit (of soortelijke weerstand) en de absorptie van lichtgolven. Daarnaast vormt het de basis van het begrip van alle vaste stof elektronica (transistoren, zonnecellen, etc.).
Banden en bandkloven[bewerken | brontekst bewerken]

De elektronen van een los, geïsoleerd atoom bevinden zich in bepaalde atomische orbitalen (in het klassieke atoommodel ook wel elektronenbanen of elektronenschillen), waarbij discrete energieniveaus horen. Wanneer twee atomen samenkomen, en daarbij een molecuul vormen, overlappen hun orbitalen.[1][2] Het Uitsluitingsprincipe van Pauli stelt dat geen enkel paar van elektronen in een molecuul dezelfde kwantumgetallen mogen hebben. Als twee identieke atomen samenkomen om een diatomisch molecuul te vormen, splitst elke atomische orbitaal in twee moleculaire orbitalen, met elk een verschillende energie, waardoor de elektronen van de oorspronkelijke atomische orbitalen zich in de nieuwe banenstructuur kunnen bevinden, zonder dat deze elektronen dezelfde energie hebben. Op eenzelfde manier geldt dat als een groot aantal N identieke atomen samenkomen om een vaste stof te vormen, zoals een kristalrooster, de elektronenschillen overlappen[1]. Aangezien het Uitsluitingsprincipe van Pauli stelt dat twee elektronen in een vaste stof nooit dezelfde kwantumgetallen mogen hebben, splitst elke atomische orbitaal in N discrete moleculaire orbitalen, elke met een andere energie. Doordat het aantal atomen in een macroscopische vaste stof een groot getal is (N~1022), is ook het aantal orbitalen erg groot en dus liggen deze energetisch zeer dicht bij elkaar (orde van grootte van 10−22 eV). De energie van naast elkaar gelegen niveaus ligt dusdanig dicht bij elkaar, dat deze kunnen worden beschouwd als een continu spectrum, een energieband. Dit proces waarbij banden gevormd worden, speelt voornamelijk een rol bij de buitenste elektronen (valentie-elektronen) van het atoom. Deze elektronen zijn verantwoordelijk voor chemische bindingen en conductiviteit (ook wel soortelijke geleidbaarheid). De binnenste elektronenschillen overlappen niet significant, dus die banden zijn erg smal. Band gap's zijn in essentie de energiegebieden die door geen enkele band bezet worden, een gevolg van de eindige breedte van de energiebanden. Banden hebben verschillende breedtes, die afhankelijk zijn van de mate van overlap van de atomische orbitalen waaruit ze ontsprongen zijn. Het is mogelijk dat twee aangrenzende banden simpelweg niet breed genoeg zijn om het volledige energiespectrum te dekken. Bijvoorbeeld, de banden die worden geassocieerd met de kern orbitalen (zoals 1s elektronen) zijn zeer smal ten gevolge van de minieme overlap tussen aangrenzende atomen. Hierdoor treden er geregeld grote energiekloven op tussen kern banden. Bij hogere banden spelen in vergelijking grotere orbitalen een rol, welke alsmaar breder worden bij hogere energieën, waardoor er geen energiekloven meer optreden bij hogere energieën.
Bandstructuur en optische eigenschappen[bewerken | brontekst bewerken]

Aangezien de energieën van elektronen in een bepaalde toestand in de energieband discreet zijn, kunnen bepaalde optische eigenschappen worden afgeleid van de bandstructuur. Doordat bij een bandisolator de valentieband vol zit, kan er enkel een foton worden opgenomen als deze een energie heeft die groter is dan de band gap. Dan wordt een elektron aangeslagen en naar de hogere energieband (geleidingsband) geëxciteerd. Het resultaat hiervan is dat fotonen met een te lage energie simpelweg niet door het materiaal geabsorbeerd worden.
Aangezien fotonen in het zichtbaar licht spectrum een energie hebben tussen de 1.8 eV en de 3.1 eV, geldt dat elk materiaal met een band gap groter dan deze energie compleet transparant oogt. Materialen zoals diamant en kwarts zijn insulatoren van dit type.
Halfgeleiders hebben daarentegen vaak kleinere band gaps, waardoor enkele fotonen in het zichtbaar licht spectrum geabsorbeerd zullen worden. Cadmiumsulfide is een halfgeleider met een band van ongeveer 2.6 eV. Dit materiaal kan dus blauw en violet licht absorberen, maar zendt rood en groen licht uit. Als gevolg hiervan krijgt het materiaal een roodachtige kleur.[3]
Voor metalen geldt deze logica niet zo eenduidig. Aangezien de banden hier ofwel overlappen, ofwel niet volledig gevuld zijn, kunnen fotonen met allerlei energieën geabsorbeerd en dus later ook geëmiteerd worden.
Basisconcepten[bewerken | brontekst bewerken]
Aannames en tekortkomingen van bandstructuur theorie.[bewerken | brontekst bewerken]
Bandtheorie is enkel een benadering van de kwantumtoestand van een vaste stof, die van toepassing is op vaste stoffen bestaande uit vele identieke atoom- en molecuulbindingen tezamen. De volgende aannames zijn voor bandtheorie noodzakelijk:
- Oneindig groot systeem: De banden zijn enkel continu als het materiaal bestaat uit een oneindig groot aantal atomen. Aangezien macroscopische materialen aantallen atomen bezitten in de orde van grootte 1022, is dit geen problematische beperking. Bandtheorie is zelfs van toepassing op microscopische elektronica zoals transistoren in geïntegreerde schakelingen. Met wat aanpassingen is het mogelijk bandtheorie toepasbaar te maken voor systemen die enkel "groot" zijn in bepaalde dimensies, zoals een tweedimensionaal elektronengas.
- Homogeen systeem: bandstructuur is een intrinsieke eigenschap van een materiaal, wat impliciet aanneemt dat het materiaal homogeen is. In de praktijk betekent dit dat de chemische basis van het materiaal uniform is door het materiaal heen.
- Geen interactie: de bandstructuur beschrijft de toestand van losse elektronen. Het bestaan van deze toestanden gaat uit van bewegende elektronen in een statisch potentiaal, zonder dynamische interacties met andere elektronen, fotonen, fononen, etc.
Bovenstaande aannames worden gebroken in een aantal belangrijke praktische situaties, en het gebruik van bandtheorie vereist dat men goed op de hoogte is van de tekortkomingen daarvan:
- Inhomogeniteiten en interfaces: dicht bij het oppervlak, verbindingspunten, en andere inhomogeniteiten, wordt de bandstructuur verstoord. Hierbij treden niet alleen lokale kleinschalige verstoringen op (gedoteerde toestanden binnen de energiekloof), maar ook lokale ladingsverstoringen. Deze ladingsverstoringen hebben elektrostatische effecten die een belangrijke rol spelen bij halfgeleiders, isolatoren en het vacuüm.
- Op dezelfde manier geldt dat vele elektrische effecten (elektrische capaciteit, elektrische weerstand, etc.) verklaard worden door de fysica van elektronen die door oppervlakten en/of surfaces bewegen. Een beschrijving van deze effecten, in het perspectief van de bandtheorie, vereist ten minste een basaal model met elektron-elektron interacties.
- Kleine systemen: Voor systemen die klein zijn langs elke dimensie (e.g. een klein molecuul of een kwantum dot) is er geen continue bandstructuur. Het gebied tussen de kleine en de grote dimensies is de wereld van de mesoscopische fysica.
- Sterk gecorreleerde materialen (e.g. Mott isolatoren) kunnen niet verklaard worden door enkele losstaande elektrontoestanden. De elektrische bandstructuur van deze materialen is slecht gedefinieerd (niet uniek gedefinieerd) en geeft dus mogelijk te weinig nuttige informatie over de fysische toestand.
Kristallijne symmetrie en golfvectoren[bewerken | brontekst bewerken]

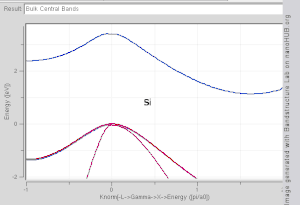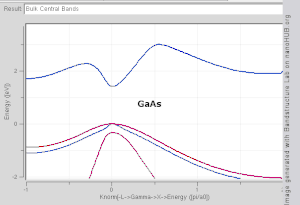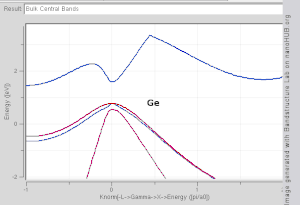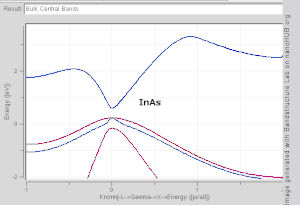
Bij het berekenen van bandstructuren wordt gebruik gemaakt van de periodieke en symmetrische eigenschappen van een kristalrooster. De Schrödingervergelijking van een enkel elektron in een rooster-periodiek potentiaal is opgelost, met Bloch golven als oplossing:
- ,
waarbij eik r een functie is, periodiek in de eenheidscel, en k de golfvector is. Voor elke waarde van k zijn er meerdere oplossingen voor de Schrödinger vergelijking, gelabeld door n, de band index, welke enkel de energiebanden nummert. Elk van deze energieniveaus verandert zeer gelijkmatig met k .Voor elke band definiëren we een functie En(k), welke de dispersierelatie voor elektronen in de betreffende band beschrijft. De golfvector kan elke waarde in de Brillouinzone aannemen. De Brillouinzone is een veelvlak in golfvector ruimte, gerelateerd aan het kristalrooster. Golfvectoren buiten de Brillouinzone corresponderen met toestanden die fysisch equivalent zijn aan toestanden binnen de Brillouinzone. Punten en lijnen met uitzonderlijk hoge symmetrie-eigenschappen in de Brillouinzone zijn de punten/lijnen aangegeven met Γ, Δ, Λ, Σ (zie Fig 3). Het is moeilijk om de vorm van een band als functie van de golfvector te visualiseren, sinds dit een vierdimensionale projectie is (E afgezet tegen kx, ky, kz). In wetenschappelijke literatuur is het daarom gebruikelijk om bandstructuurprojecties tegen te komen die waardes van En(k) voor k te laten zien langs rechte lijnen die symmetriepunten verbindt, vaak aangegeven met Δ, Λ, Σ, of [100], [111], [110], respectievelijk.[4][5] Een andere methode waarmee de bandstructuur kan worden gevisualiseerd is door een constant energie iso-oppervlak te projecteren in golfvector-ruimte. Een dergelijke diagram geeft alle toestanden waarbij de energie gelijk is aan een bepaalde waarde. Het iso-oppervlak van toestanden met het energieniveau gelijk aan het Fermi-niveau wordt het Fermi-oppervlak genoemd. Energiekloven kunnen geclassificeerd worden door gebruik te maken van de golfvectoren van toestanden rondom de band gap:
- Directe band gap: de laagste energietoestand boven de band gap heeft dezelfde golfvector k als de hoogste energietoestand onder de band gap.
- Indirecte band gap: de dichtstbijzijnde toestand boven en onder de band gap hebben niet dezelfde golfvector k.
Toestandsdichtheid[bewerken | brontekst bewerken]
De functie waarmee de toestandsdichtheid g(E) wordt beschreven is gedefinieerd als het aantal elektrische toestanden per volume-eenheid, voor elektronenergieën dicht bij E Deze toestandsdichtheid-vergelijking is belangrijk voor het berekenen van gevolgen gebaseerd op de bandtheorie. Voor Fermi's gulden regel, een berekening voor de snelheid van lichtabsorptie, verschaft het zowel het aantal elektronen die aangeslagen kunnen worden, als het aantal uiteindelijke toestanden van een elektron. Ook komt de toestandsdichtheid-vergelijking voor in berekeningen van elektrische conductiviteit. Aangezien elektronen niet in een toestand in de band gap kunnen verkeren, geldt g(E) = 0.
Vullen van banden[bewerken | brontekst bewerken]

Voor een thermodynamisch evenwicht geldt dat de waarschijnlijkheid dat een toestand met energie E wordt gevuld (lees: bezet) door een elektron gegeven wordt door de Fermi-dirac verdeling, een thermodynamische verdeling die rekening houdt het met het Uitsluitingsprincipe van Pauli:
waar:
- kBT het product van de constante van Boltzmann en de temperatuur is, en
- µ het chemische potentiaal van de elektronen is, ofwel het Fermi-niveau (in halfgeleider fysica wordt dit vaak aangeduid met EF).
De elektronendichtheid in het materiaal is simpelweg de integraal van de Fermi-dirac verdeling maal de toestandsdichtheid:
Hoewel er oneindig veel banden en dus ook oneindig veel toestanden zijn, zijn er slechts een eindig aantal elektronen die deze banden kunnen vullen. Deze hoeveelheid elektronen volgt uit een principe van de elektrostatica: hoewel het oppervlak van een materiaal geladen kan zijn, geldt dat de interne bulk van een materiaal elektrisch neutraal wil zijn. Deze voorkeur van neutraliteit betekent dat N/V overeenkomt met de toestandsdichtheid van protonen in het materiaal. Om ervoor te zorgen dat dit daadwerkelijk zo is, past het materiaal zichzelf elektrostatisch aan, waarbij diens bandstructuur omhoog of omlaag verschoven wordt in energie, totdat het juiste evenwicht ten opzichte van het Fermi-niveau bereikt is.
Banden dicht bij het Fermi-niveau[bewerken | brontekst bewerken]
Een vaste stof heeft een oneindig aantal banden, net zoals dat een atoom oneindig veel energieniveaus heeft. Echter, de meeste banden hebben een te hoge energie en worden daarom gewoonlijk buiten beschouwing gelaten.[6] De lage energie banden worden geassocieerd met de kern orbitalen (zoals de 1s elektronen). Deze lage energie kernbanden kunnen ook gewoonlijk buiten beschouwing worden gelaten omdat ze te allen tijde gevuld, en daarom onveranderd, zullen blijven. De meest belangrijke banden en band gaps – die relevant zijn voor elektronica en opto-elektronica – hebben energieën dicht bij het Fermi-niveau. Deze banden en band gaps hebben speciale benamingen gekregen, afhankelijk van het materiaal, en geven een verklaring voor de conductiviteit van het materiaal.[7]
- In een halfgeleider of band isolator wordt het Fermi-niveau omringd door een band gap die dé band gap wordt genoemd (hiermee is het te onderscheiden van andere band gaps in de toekomst). De dichtstbijzijnde band boven de band gap heet de geleidingsband, de dichtstbijzijnde band onder de band gap heet de valentieband. Voor een isolator geldt dat de valentieband volledig gevuld is met elektronen en de geleidingsband leeg is. Aangezien er een band gap aanwezig tussen de top van de valentieband en het dal van de geleidingsband, kunnen elektronen niet makkelijk van de valentie- naar de geleidingsband springen. Als het materiaal nu in een klein elektrisch veld wordt gebracht, kan het systeem niet reageren - er is simpelweg geen plek voor de elektronen om naartoe te gaan: het materiaal geleidt niet. (zie Fig 5)
- In een metaal of halfmetaal ligt het Fermi-niveau in een of meerdere toegestane banden. In een halfmetaal worden deze banden gewoonlijk de geleidings- of valentiebanden genoemd, afhankelijk van of de manier waarop de lading beweegt, berust of de beweging van elektronen of elektronengaten. Het Fermi-niveau ligt in een of meerdere banden, er zal dus een band niet volledig gevuld zijn. Als het materiaal nu in een klein elektrisch veld wordt gebracht, kunnen de elektronen hergroeperen en daarmee kan er een stroom lopen. Ze kunnen immers met "extreem" kleine energieverschillen een andere toestand aannemen binnen de band: het materiaal geleidt. (zie Fig 5)
Bandstructuren in kristallen[bewerken | brontekst bewerken]
De ansatz is het speciale geval van een elektrongolf in een periodieke kristalrooster gebruik makend van Bloch golven, zoals deze worden behandeld in de dynamische diffractietheorie. Elk kristal bezit een periodieke structuur welke kan worden gekarakteriseerd door een Bravaistralie, en voor elke Bravaistralie kunnen we een reciprook rooster bepalen, welke de periodiciteit met een basis van drie reciproke vectoren (b1,b2,b3) kan beschrijven. Welnu, elk periodieke potentiaal V(r) dat dezelfde periodiciteit heeft als het directe rooster kan worden beschreven door een Fourierreeks waarvan de enige componenten die niet wegvallen de componenten geassocieerd met het reciproke rooster zijn. Dus het potentiaal kan worden geschreven als:
waarbij K = m1b1 + m2b2 + m3b3 voor elke set gehele getallen (m1,m2,m3). Vanuit deze theorie is het mogelijk te proberen om de bandstructuur van een specifiek materiaal te voorspellen. Echter, de meeste ab initio methoden gebruikt om deze structuren te voorspellen, blijken tekort te schieten in het voorspellen van de band gap’s.
Bijna-vrije elektron benadering[bewerken | brontekst bewerken]
In de bijna-vrije elektron benadering worden interacties tussen elektronen volledig buiten beschouwing gelaten. Deze benadering laat gebruik van de Stelling van Bloch toe, welke zegt dat elektronen in een periodiek potentiaal golffuncties en energieën hebben die periodiek in golfvector zijn, tot een constante faseverschuiving tussen aangrenzende reciproke vectoren. Wiskundig gezien geldt dan dat
waar de functie periodiek is over het kristalrooster, oftewel,
- .
Hierbij indexeert n de ne energieband, is de golfvector k gerelateerd aan de beweging van het elektron, is r de positie in het kristal, en is R de locatie van een atomair roosterpunt.[8] Het bijna-vrije elektron model werkt bij uitstek goed in materialen zoals metalen, waarbij afstanden tussen aangrenzende atomen klein zijn. In zulke materialen geldt dat de overlap van atomaire orbitalen en potentialen van aangrenzende atomen relatief groot is. In dat geval kan de golffunctie van het elektron benaderd worden door een (gemodificeerde)vlakke golf. De bandstructuur van een metaalachtige zoals aluminium komt zelfs zeer goed overeen met het de lege roosterbenadering.
Referenties[bewerken | brontekst bewerken]
- ↑ a b Holgate, Sharon Ann (2009). Understanding Solid State Physics. CRC Press, 177–178. ISBN 1420012320.
- ↑ Van Zeghbroeck, B. , 2011, Section 2.3: Energy Bands. Principles of Semiconductor Devices. Electrical, Computer, Energy Engineering Dept., Univ. of Colorado at Boulder (2011). Gearchiveerd op 20 mei 2017. Geraadpleegd op March 13, 2017.
- ↑ Simon, Steven H. (2013). The Oxford Solid State Basics. Oxford University Press, 179. ISBN 9782199682764. Geraadpleegd op 18 februari 2018.
- ↑ Band structure and carrier concentration
- ↑ Electronic Band Structure. www.springer.com. Springer. Geraadpleegd op 10 november 2016.
- ↑ Hoge energiebanden zijn belangrijk bij elektronendiffractie , waar elektronen met hoge energieën op een materiaal kunnen worden afgevuurd. Zie Stern, R., Perry, J., Boudreaux, D. (1969). Low-Energy Electron-Diffraction Dispersion Surfaces and Band Structure in Three-Dimensional Mixed Laue and Bragg Reflections. Reviews of Modern Physics 41 (2): 275. DOI: 10.1103/RevModPhys.41.275. .
- ↑ Simon, Steven H. (2013). The Oxford Solid State Basics. Oxford University Press, 104. ISBN 9782199682764. Geraadpleegd op 18 februari 2018.
- ↑ Kittel, Charles (2005). Introduction to Solid State Physics. John Wiley & Sons, Inc., 179. ISBN 1420012320. Geraadpleegd op 18 februari 2018.
Bibliografie[bewerken | brontekst bewerken]
- Charles Kittel (1996). Introduction to Solid State Physics, Seventh. Wiley, New York. ISBN 0-471-11181-3.







