Stelling over homomorfismen
In de abstracte algebra, een deelgebied van de wiskunde, legt de stelling over homomorfismen het verband tussen de structuur van twee wiskundige objecten, waartussen een homomorfisme is gegeven, en de kern en het beeld van het homomorfise.
De stelling over homomorfismen worden gebruikt om de isomorfismestellingen te bewijzen.
Groepstheoretische versie[bewerken]
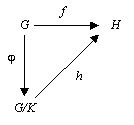
Laat, gegeven twee groepen G en H en een groepshomomorfisme f : G → H, K een normaaldeler in G zijn en laat φ het natuurlijke surjectieve homomorfisme G → G/K zijn.
Als K ⊂ ker (f), dan bestaat er een uniek homomorfisme h: G/K → H zodanig dat f = h φ.
De situatie wordt beschreven door het onderstaande commutatieve diagram
Door het instellen van K = ker(f) hebben we meteen de eerste isomorfismestelling te pakken.
Andere versies[bewerken]
Soortgelijke stellingen zijn er voor monoïdes, vectorruimten, modules en ringen.
