Vectorruimte
Een vectorruimte, ook lineaire ruimte genoemd, is een wiskundige structuur die wordt gevormd door een verzameling elementen die vectoren worden genoemd, die bij elkaar kunnen worden opgeteld en die kunnen worden vermenigvuldigd met getallen die in deze context scalairen worden genoemd. Vaak zijn de scalairen reële getallen, maar er bestaan ook vectorruimten waarin de scalairen complexe getallen, rationale getallen of heel algemeen elementen van een willekeurig veld (Vlaams) of lichaam (Nederlands) zijn. Dat hangt van de definitie af. De operaties van vectoroptelling en scalaire vermenigvuldiging moeten aan bepaalde eisen voldoen, de zogenaamde axioma's.
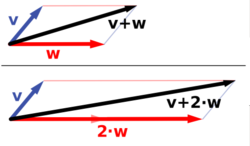
De euclidische vectorruimte is voor elke dimensie een voorbeeld van een vectorruimte. De twee- en driedimensionale euclidische vectorruimte worden vaak gebruikt om natuurkundige grootheden, zoals krachten weer te geven: elke twee krachten (van hetzelfde type) kunnen worden opgeteld met als resultaat een derde kracht, de resultante, en de scalaire vermenigvuldiging van een krachtvector met een reële factor is opnieuw een krachtvector. Als meer meetkundig voorbeeld, vormen vectoren die translaties in het vlak of in de driedimensionale ruimte weergeven, ook vectorruimten.
Vectorruimten vormen een belangrijk onderwerp van studie binnen de lineaire algebra. De theorie wordt verder verrijkt door aan een vectorruimte extra structuur, zoals een norm of een inwendig product, toe te kennen. Zulke vectorruimten komen van nature voor in de wiskundige analyse, vooral in de gedaante van oneindig-dimensionale functieruimten waarvan de vectoren functies zijn. Een belangrijke vraag is of een rij vectoren naar een bepaalde vector convergeert. Het antwoord op deze vraag kan worden gegeven door vectorruimten met aanvullende gegevens te bestuderen, meestal vectorruimten die zijn uitgerust met een gepaste topologie, die het mogelijk maakt om begrippen als afstand en continuïteit in beschouwing te nemen. Dit soort verrijkte topologische vectorruimten, met name banachruimten en hilbertruimten, hebben een rijkere theorie.
Historisch gesproken kunnen de eerste ideeën die hebben geleid tot vectorruimten, teruggevoerd worden tot de 17e-eeuwse analytische meetkunde, matrices, stelsels lineaire vergelijkingen en euclidische vectoren. De moderne, meer abstracte behandeling werd in de late 19e eeuw voor het eerst door Giuseppe Peano geformuleerd en omvat meer algemene objecten dan de euclidische ruimte. Veel van de theorie kan worden gezien als een uitbreiding van de klassieke meetkundige ideeën, zoals lijnen, vlakken en hun hogerdimensionale generalisaties.
Vectorruimten vindt men in de gehele wiskunde, de natuurwetenschappen en de technische wetenschappen. Zij vormen het geschikte algebraïsche begrip om met stelsels lineaire vergelijkingen om te gaan. Ook bieden zij een raamwerk voor de fourierreeksen, die worden gebruikt in algoritmen voor beeldcompressie, en bieden zij een omgeving die kan worden gebruikt voor oplossingstechnieken voor partiële differentiaalvergelijkingen. Bovendien leveren vectorruimten een abstracte manier van omgaan met meetkundige en natuurkundige objecten, zoals tensoren, die op hun beurt het onderzoek van de lokale eigenschappen van variëteiten door linearisatietechnieken mogelijk maken. Het begrip vectorruimte kan ook in verschillende richtingen worden gegeneraliseerd, wat tot geavanceerde begrippen leidt in de meetkunde en de abstracte algebra.
| Algebraïsche structuur | |
|
Groep · Halfgroep · Ideaal · Lichaam/veld · Magma · Monoïde · Ring |
Geschiedenis[bewerken | brontekst bewerken]
Het begrip vectorruimte vloeit uit de affiene meetkunde voort, via de introductie van coördinaten in het platte vlak of in de gebruikelijke driedimensionale ruimte. De Franse wiskundigen Descartes en Fermat legden rond 1636 de basis voor de analytische meetkunde door de oplossingen van een vergelijking met twee variabelen te koppelen aan het verloop van een tweedimensionale kromme.
Bernard Bolzano introduceerde in 1804 bepaalde operaties op punten, lijnen en vlakken die als voorlopers van vectoren kunnen worden gezien.[1] Hij deed dat om zonder van coördinaten gebruik te maken tot een meetkundige oplossing te komen. Möbius heeft dit werk in 1827 geanalyseerd en werkte daarbij met barycentrische coördinaten.[2] De beslissende stap in de definitie van vectoren was Bellavitis' definitie van het bipunt: een richtinggevend segment waarvan een van de uiteinden de oorsprong is en de ander het doel.
Vectorruimten werden in een nieuw licht geplaatst door de introductie van het complexe vlak door Jean-Robert Argand en William Rowan Hamilton en de introductie van quaternionen en octonionen door de laatstgenoemde. De lineaire combinatie is een idee van Laguerre uit 1867, die in dat jaar stelsels lineaire vergelijkingen definieerde.
Cayley introduceerde in 1857 zijn matrixnotatie, die het mogelijk maakte de notatie van lineaire afbeeldingen tussen vectorruimten te vereenvoudigen.
Grassmann rekende tegelijkertijd met barycentrische coördinaten, die door Möbius waren ingevoerd, en waarmee hij verzamelingen van wiskundige objecten, uitgerust met operaties, onderzocht.[3] Zijn werk ging verder dan de lineaire algebra en met de manier waarop hij de vermenigvuldiging behandelde voerde hij algebra's in. De begrippen dimensie en lineaire onafhankelijkheid komen in zijn werk voor, evenals het inwendige product, 1844. Cauchy vocht het in zijn publicatie Sur les clefs algébriques aan dat Grassmann het eerste met deze ideeën was gekomen.
De Italiaanse wiskundige Peano, die er veel aan heeft bijgedragen de wiskunde op axioma's terug te voeren, vooral in de verzamelingenleer, was een van de eersten die rond het einde van de 19de eeuw met de moderne definitie van vectorruimten werkte.[4]
Een belangrijke ontwikkeling van de vectorruimten is te danken aan de constructie van functieruimten door Henri Lebesgue. Deze theorie werd later door David Hilbert en Stefan Banach nauwkeurig beschreven, in zijn proefschrift uit 1920. De algebra en het nieuwe terrein van de functionaalanalyse begonnen op dit moment op elkaar in te werken, met belangrijke ideeën zoals ruimten van -integreerbare functies en hilbertruimten. De eerste studies naar oneindig-dimensionale vectorruimten werden ook in die tijd uitgevoerd.
Definitie[bewerken | brontekst bewerken]
Een vectorruimte over een lichaam (Ned) / veld (Be) is een verzameling van elementen, aangeduid als vectoren, waarop twee bewerkingen zijn gedefinieerd: een som van twee vectoren, genoteerd met , en een scalaire vermenigvuldiging van een element uit een scalair met een vector, genoteerd met of , vaak wordt de operator ook weggelaten. Deze bewerkingen moeten voldoen aan de volgende voorwaarden:
Voor alle drie al dan niet verschillende vectoren en twee scalairen geldt:
- is weer een vector in ,
is gesloten onder de optelling van vectoren -
De optelling van vectoren is associatief. - Er bestaat een element , zo dat voor alle vectoren geldt: .
Het element wordt het additieve identiteit of de nulvector genoemd. Men kan aantonen dat de additieve identiteit uniek is. Aangezien het zelden tot verwarring aanleiding geeft, schrijft men ook alleen 0 in plaats van . - Voor alle vectoren bestaat er een vector zo dat
De vector noemt men het inverse element of de tegengestelde vector van . -
De optelling van vectoren is commutatief. - is weer een vector uit
is gesloten onder de scalaire vermenigvuldiging. -
De scalaire vermenigvuldiging is gemengd associatief. - Als 1 het neutrale element is van voor de scalaire vermenigvuldiging, geldt .
-
De scalaire vermenigvuldiging is distributief over de optelling van vectoren. -
De scalaire vermenigvuldiging is distributief over de optelling van scalairen.
Merk op dat het optellen van twee scalairen in en van twee vectoren in verschillende bewerkingen zijn.
De eigenschappen 1 t/m 5 zijn equivalent met de eigenschap dat een abelse of commutatieve groep is onder de optelling. Door te vervangen door een willekeurige ring , vormen de voorwaarden de definitie van een R-moduul. Een vectorruimte is een soort moduul.
Uit de definitie volgt onder meer:
- dan en slechts dan als of
Een vectorruimte waarop een norm is gedefinieerd, heet een genormeerde vectorruimte.
Reële en complexe vectorruimte[bewerken | brontekst bewerken]
Veelgebruikte vectorruimten zijn die waarin de reële getallen of de complexe getallen is. De vectorruimte heet dan een reële en een complexe vectorruimte. "Complex" slaat dus op , niet op : de vectorruimte met reële scalairen is een (weliswaar vrij ongebruikelijke) reële vectorruimte, isomorf met . Het omgekeerde, met complexe scalairen, is met de gebruikelijke definitie van de scalaire vermenigvuldiging niet mogelijk.
Voortbrengend deel, vrij deel, basis en dimensie[bewerken | brontekst bewerken]
Men zegt dat een verzameling vectoren een voortbrengend deel van een vectorruimte is, als de kleinste vectorruimte is die bevat. Dit houdt niet alleen in dat alle lineaire combinaties van vectoren uit bevat, maar ook dat alle vectoren in lineaire combinaties zijn van vectoren uit .
Het stelsel vectoren heet een vrij deel als de vectoren uit lineair onafhankelijk zijn, dus als:
Dit wil zeggen dat de enige lineaire combinatie van vectoren in die nul oplevert, de combinatie is met alle coëfficiënten nul. Het gevolg is dat verschillende lineaire combinaties van vectoren in ook verschillende vectoren voorstellen.
Een basis van is een deelverzameling die zowel een voortbrenger van is als een vrij deel in . Men kan (onder aanname van het keuzeaxioma) aantonen dat elke vectorruimte een basis heeft. Intuïtief beschouwd is een basis een zo klein mogelijke verzameling van vectoren waarmee de hele vectorruimte opgebouwd kan worden, door scalaire vermenigvuldigingen en vectorsommen. In een gegeven vectorruimte kan een basis op verschillende manieren worden gekozen, maar het aantal vectoren in een basis van , de kardinaliteit ervan, is altijd gelijk.
Het aantal vectoren van de basis wordt de dimensie van de vectorruimte genoemd. Intuïtief beschouwd is de dimensie van een vectorruimte het aantal onderling onafhankelijke richtingen in de vectorruimte.
Als het lichaam eindig is, geldt:
- bij een eindige basis is eindig,
- bij een aftelbaar oneindige basis is aftelbaar oneindig.
Deelruimte[bewerken | brontekst bewerken]
Een deelruimte of lineaire deelruimte is een deelverzameling van een vectorruimte die zelf ook weer een vectorruimte over hetzelfde lichaam is. Elke vectorruimte bevat twee triviale deelruimtes: zichzelf en ook de kleinst mogelijke deelruimte, die alleen uit de nulvector bestaat.
Voorbeelden[bewerken | brontekst bewerken]
Coördinaten- en functieruimten[bewerken | brontekst bewerken]
Een voorbeeld van een vectorruimte over een lichaam/veld is de coördinatenruimte , waarvan de elementen -tupels zijn, rijen van lengte van elementen .[5] Bij een gegeven -dimensionale vectorruimte over correspondeert met iedere basis een isomorfisme met . Zowel de kolom- als de rijvectoren van de betreffende lengte vormen ook zo'n isomorfe vectorruimte.
Meer in het algemeen vormen functies van elke vaste verzameling naar een lichaam/veld (het product van een geïndexeerde familie van gelijke vectorruimten , met indexverzameling ) ook vectorruimten, door de optelling en de scalaire vermenigvuldiging puntsgewijze uit te voeren. Dat wil zeggen dat de som van twee functies en wordt gegeven door
en de scalaire vermenigvuldiging door:
- .
Met wordt de verzameling bedoeld van alle functies . Daarmee komt het cartesisch product overeen met Als een oneindige verzameling is, is een oneindigdimensionale vectorruimte. De ruimte , ook genoemd, is de ruimte van alle oneindige rijen van elementen in . De verzameling kan ook overaftelbaar zijn, bijvoorbeeld het interval zodat de ruimte is van alle functies op dit interval. Bij oneindige wordt in veel gevallen alleen een deelruimte beschouwd, bijvoorbeeld rijen of functies met eindige drager, of Lp, een genormeerde vectorruimte. De verzameling functies en de norm worden in samenhang met elkaar gekozen, zodat de norm nooit oneindig wordt.
Zulke functieruimten komen in veel situaties in de meetkunde voor, bijvoorbeeld als de reële lijn, een interval, of andere deelverzamelingen van voorstelt. Veel begrippen uit de topologie en de analyse, zoals continuïteit, integreerbaarheid of differentieerbaarheid gedragen zich goed met betrekking tot de lineariteit: optellen en het nemen van een scalair veelvoud van functies, die een dergelijk eigenschap bezitten, beschikken na deze bewerking nog steeds over deze eigenschap.[6] Daarom zijn dergelijke verzamelingen van functies vectorruimten. Zij worden meer in detail bestudeerd door gebruik te maken van de methoden uit de functionaalanalyse. Algebraïsche beperkingen leveren ook vectorruimten op: de veeltermring , zowel een vectorruimte als een ring, wordt gegeven door de verzameling van alle polynomen, dus van willekeurige graad :
- , met de coëfficiënten .[7]
Lineaire vergelijkingen[bewerken | brontekst bewerken]
Stelsels van lineaire vergelijkingen die homogeen zijn, zijn nauw verbonden aan vectorruimten.[8] De oplossingen van
worden bijvoorbeeld gegeven door drietallen met en . Deze drietallen vormen een vectorruimte: optellingen en scalaire veelvouden voldoen steeds aan dezelfde verhoudingen van de drie variabelen, dus zijn zij oplossingen voor het stelsel van vergelijkingen. Om lineaire vergelijkingen, zoals hierboven, compacter op te schrijven, kan men gebruikmaken van matrices, bijvoorbeeld
waarin
de matrix is die de coëfficiënten van de gegeven vergelijkingen bevat, de kolomvector de onbekenden bevat, de nulvector is, en de matrixvermenigvuldiging van en .
De oplossingen van een homogene lineaire differentiaalvergelijking vormen ook een vectorruimte. De vergelijking
bijvoorbeeld heeft als oplossingen de functies
- ,
waarin en willekeurige constanten zijn.
Uitbreidingen[bewerken | brontekst bewerken]
Lichaams-/velduitbreidingen , uitgesproken over , vormen een andere klasse van vectorruimten, met name in de algebra en de algebraïsche getaltheorie: een lichaam/veld dat een uitbreiding is van wordt onder de gegeven vermenigvuldiging en optellingsoperaties van een -vectorruimte.[9] De complexe getallen zijn bijvoorbeeld een vectorruimte over . Een bijzonder interessant type velduitbreiding in de getaltheorie is , de uitbreiding van de rationale getallen met een gegeven complex getal . is het kleinste lichaam/veld dat de rationale en een gegeven complex getal bevat. De dimensie als een vectorruimte over is afhankelijk van de keuze van .
Een moduul is een algebraïsche structuur die erg lijkt op een vectorruimte. Een moduul is echter gedefinieerd over een ring, in plaats van over een lichaam/veld. Bij een moduul eist men dus niet dat een lichaam/veld is, maar wel dat een ring is. Elke vectorruimte is dus een moduul en alle eigenschappen van modulen gelden ook voor vectorruimten.
Literatuur[bewerken | brontekst bewerken]
Lineaire algebra[bewerken | brontekst bewerken]
- (en) Serge Lang. Linear algebra, Springer-Verlag, Berlijn, New York, ISBN 978-0-387-96412-6, 1987
- (en) Serge Lang. Algebra, Graduate Texts in Mathematics, 211 (Revised third ed.), New York: Springer-Verlag, MR1878556, ISBN 978-0-387-95385-4, 2002
Analyse[bewerken | brontekst bewerken]
- (en) Serge Lang. Real analysis, Addison-Wesley, ISBN 978-0-201-14179-5, 1983
- (en) Serge Lang. Real and functional analysis, Berlijn, New York: Springer-Verlag, ISBN 978-0-387-94001-4, 1993
Historisch[bewerken | brontekst bewerken]
- (fr) Stefan Banach. Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (On operations in abstract sets and their application to integral equations) zie hier, Fundamenta Mathematicae, ISSN 0016-2736, vol 3, 1922
- (de) Bernard Bolzano. Betrachtungen über einige Gegenstände der Elementargeometrie (Considerations of some aspects of elementary geometry) zie hier, 1804
- (de) Hermann Grassmann. Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik, zie hier, O. Wigand, 1844
- (de) August Ferdinand Möbius. Der Barycentrische Calcul : ein neues Hülfsmittel zur analytischen Behandlung der Geometrie (Barycentric calculus: a new utility for an analytic treatment of geometry) zie hier, 1827
- (it) Giuseppe Peano. Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva, Turijn, 1888
Voetnoten[bewerken | brontekst bewerken]
- ↑ Bernard Bolzano, Betrachtungen über einige Gegenstände der Elementargeometrie, 1804.
- ↑ August Ferdinand Möbius. Der Barycentrische Calcul: ein neues Hülfsmittel zur analytischen Behandlung der Geometrie, 1827.
- ↑ Hermann Grassmann. Extension Theory, 2000. voor de American Mathematical Society ISBN 978-0-8218-2031-5
- ↑ Giuseppe Peano. Calcolo Geometrico, 1888. op Google Books
- ↑ Serge Lang, 1987. hoofdstuk I.1
- ↑ Serge Lang, 1993. hoofdstuk XII.3, blz 335
- ↑ Serge Lang. 1987. hoofdstuk IX.1
- ↑ Serge Lang. 1987 hoofdstuk VI.3.
- ↑ Serge Lang. 2002, hoofdstuk V.1























































![{\displaystyle [0,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/971caee396752d8bf56711f55d2c3b1207d4a236)
![{\displaystyle K^{[0,1]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38b26ef863f9dd900adfe2c4f783dfdefa42c339)
![{\displaystyle K[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a9e6c2ac2830d6a9abe078b47450777c41d69a9)





















