Groep (wiskunde)

In de groepentheorie, een deelgebied van de wiskunde, is een groep een algebraïsche structuur die bestaat uit een verzameling en een binaire operatie, de groepsbewerking, die aan twee elementen van weer een element van toevoegt. De verzameling en de groepsbewerking moeten voldoen aan enkele voorwaarden, de groepsaxioma's. Er zijn er vier: de groepsbewerking is gesloten en associatief, er is in de groep een neutraal element voor de groepsbewerking, de identiteit, en ieder element in de groep heeft een invers element. Een voorbeeld van een groep vormen de gehele getallen met optellen als operatie.
De axioma's gelden voor alle groepen, maar groepen onderling kunnen heel verschillend zijn. Zij vormen het onderwerp van de groepentheorie. Met groepen kunnen de structurele aspecten van objecten van uiteenlopende oorsprong op uniforme wijze worden bestudeerd. De alomtegenwoordigheid van de groepen op tal van gebieden, zowel binnen als buiten de wiskunde, maakt van groepen een centraal ordenend principe binnen de hedendaagse wiskunde.[1][2]
Groepen delen een fundamentele verwantschap met het begrip symmetrie. Een symmetriegroep beschrijft symmetrie-eigenschappen van een meetkundig object, dus bestaat uit de verzameling van transformaties die het object ongewijzigd laten met daarbij als operatie het na elkaar uitvoeren van twee van zulke transformaties. Zulke symmetriegroepen, in het bijzonder de continue lie-groepen, spelen een belangrijke rol in tal van academische disciplines. Matrixgroepen worden bijvoorbeeld gebruikt om symmetrieën in de moleculaire scheikunde en symmetrie in de natuurkunde, zoals de natuurwetten die ten grondslag liggen aan de speciale relativiteitstheorie, te begrijpen.
De studie van vergelijkingen heeft aan de basis van de groepentheorie gestaan. Évariste Galois was in de jaren 1830 een van de wiskundigen die hieraan rekenden. De theorie die het verband legt tussen polynomen en groepen, is naar hem genoemd. Na bijdragen vanuit andere gebieden, zoals de getaltheorie en de meetkunde, kreeg het begrip groep in de wiskunde zijn algemene vorm, en kreeg de groepentheorie rond 1870 een stevige basis. Om groepen te onderzoeken hebben wiskundigen verschillende begrippen gedefinieerd die het mogelijk maken om groepen op te breken in kleinere, beter begrijpelijke stukken, zoals ondergroepen, factorgroepen en enkelvoudige groepen. Naast de abstracte eigenschappen van groepen bestuderen groepstheoretici ook de verschillende manieren waarop een groep concreet kan worden uitgedrukt, haar groepsrepresentatie, zowel vanuit een theoretisch als een computationeel standpunt. Er heeft zich een bijzondere rijke theorie van de eindige groepen ontwikkeld, die culmineerde in de classificatie van eindige enkelvoudige groepen, die werd voltooid in 1983. Sinds het midden van de jaren 1980 is de meetkundige groepentheorie, die eindig gegenereerde groepen als meetkundige objecten bestudeert, uitgegroeid tot een bijzonder actief onderzoeksgebied binnen de groepentheorie.
| Algebraïsche structuur | |
|
Groep · Halfgroep · Ideaal · Lichaam/veld · Magma · Monoïde · Ring |
Geschiedenis[bewerken | brontekst bewerken]
Het moderne concept van een abstracte groep ontwikkelde zich uit verschillende deelgebieden van de wiskunde[3][4][5]. De oorspronkelijke motivatie voor de groepentheorie was de zoektocht naar oplossingen van polynomiale vergelijkingen van graad 5 en hoger. De 19e-eeuwse Franse wiskundige Évariste Galois, die voortbouwde op eerder werk van Paolo Ruffini en Joseph-Louis Lagrange, gaf een criterium voor de oplosbaarheid van bepaalde veeltermvergelijkingen in termen van symmetriegroepen van zijn wortels (oplossingen). De elementen van een dergelijke Galoisgroep komen overeen met bepaalde permutaties van de wortels. Aanvankelijk werden Galois zijn ideeën verworpen door zijn tijdgenoten en zijn werken werden pas voor het eerst ruim vijftien jaar na zijn vroege dood gepubliceerd[6][7]. Meer algemene permutatiegroepen werden met name onderzocht door Augustin Louis Cauchy. Arthur Cayleys On the theory of groups, as depending on the symbolic equation θn = 1 (Over de groepentheorie, afhankelijk van de symbolische vergelijking θn = 1) (1854) geeft de eerste abstracte definitie van een eindige groep[8].
De meetkunde was een tweede terrein, waarop systematisch groepen werden gebruikt, vooral symmetriegroepen, als onderdeel van Felix Kleins Erlanger Programm uit 1872[9]. Nadat "nieuwe meetkunden", zoals de hyperbolische- en de projectieve meetkunde waren ontstaan, gebruikte Klein de groepentheorie om deze "nieuwe meetkunden" op een meer coherente manier te organiseren. Deze ideeën verder bevorderend, legde Sophus Lie in 1884 het fundament voor de studie van de naar hem genoemde Lie-groepen[10]
Het derde veld dat bijdroeg aan de groepentheorie was de getaltheorie. Van bepaalde abelse groep structuren werd reeds impliciet gebruikgemaakt in Carl Friedrich Gauss' Disquisitiones Arithmeticae uit 1798 en meer expliciet door Leopold Kronecker[11]. In 1847 leidde Ernst Kummer vroege pogingen om de laatste stelling van Fermat te bewijzen naar een climax door de ontwikkeling van groepen die factorisatie in priemgetallen beschreven.[12]
De convergentie van deze verschillende bronnen in een uniforme groepentheorie begon in 1870 met Camille Jordans Traité des substitutions et des équations algébriques[13]. Walther von Dyck (1882) stelde als eerste een moderne definitie van een abstracte groep[14] op. Vanaf het begin van de 20e eeuw, verkregen groepen een brede erkenning door het baanbrekende werk van Ferdinand Georg Frobenius en William Burnside, die werkte op het gebied van de representatietheorie van eindige groepen, Richard Brauers modulaire representatietheorie en de artikelen van Issai Schur[15] De theorie van de Lie-groepen, en meer in het algemeen de lokaal compacte groepen werd gepropageerd door Hermann Weyl, Élie Cartan en vele anderen[16]. Haar algebraïsche tegenhanger, de theorie van de algebraïsche groepen, werd vanaf de late jaren dertig voor het eerst door Claude Chevalley vormgegeven en later voortgezet met belangrijk werk van Armand Borel en Jacques Tits[17].
Het door de Universiteit van Chicago in het academisch jaar 1960-61 georganiseerde "Groepentheoriejaar" bracht een aantal vooraanstaande groepentheoretici, zoals Daniel Gorenstein, John Griggs Thompson en Walter Feit bij elkaar. Hierdoor werd het fundament van een samenwerking gelegd die, met inbreng van vele andere wiskundigen, in 1982 tot de classificatie van alle eindige enkelvoudige groepen zou leiden. Dit project overtrof alle vorige wiskundige inspanningen door zijn enorme omvang, zowel wat betreft de lengte van het bewijs als door het aantal onderzoekers. Er is nog steeds onderzoek gaande om het bewijs van deze classificatie te vereenvoudigen[18]. Deze dagen is de groepentheorie nog steeds een zeer actief deelgebied van de wiskunde met een cruciale invloed op vele andere takken van de wiskunde.
Definitie[bewerken | brontekst bewerken]
Een groep wordt gevormd door een niet-lege verzameling met een associatieve binaire operatie , een voor de bewerking neutraal element en bij elk element een voor de bewerking invers element .
Uitgebreider geformuleerd:
Een groep is een verzameling , samen met een operatie die aan elke twee elementen en een element toevoegt. Het is gebruikelijk te noteren als . Het symbool is een algemene plaatshouder voor een concreet gegeven operatie, zoals de optelling hierboven. De verzameling en de operatie moeten voldoen aan vier eisen die samen bekendstaan als de groepsaxioma's:[19]
- De groep is gesloten met betrekking tot de groepsbewerking: Voor alle is het resultaat van de groepsoperatie ook in .
- De groepsbewerking is associatief: Voor alle geldt de relatie: .
- Er is een identiteitselement voor de groepsbewerking: Er bestaat een element , zodat voor alle elementen geldt dat
- Bij ieder element is er een invers element: Voor elke bestaat er een element , waarvoor geldt: .
Merk op dat een groep niet noodzakelijk commutatief hoeft te zijn. Het is niet noodzakelijk dat voor alle geldt dat . Als dit wel het geval is spreekt men van een commutatieve of abelse groep, genoemd naar de wiskundige Niels Abel.
Verder wordt er onderscheid gemaakt tussen eindige en oneindige groepen.
Voorbeelden[bewerken | brontekst bewerken]
- De gehele getallen met de optelling, genoteerd als , is een abelse groep.
- De rationale getallen zonder de nul met de vermenigvuldiging (, · ) is een abelse groep.
- De natuurlijke getallen met de optelling is geen groep, want bijvoorbeeld 2 heeft geen inverse, omdat er geen natuurlijk getal is dat opgeteld bij 2 als resultaat 0 oplevert.
- Permutatiegroepen en matrixgroepen
- De mogelijke manipulaties van de Rubiks kubus vormen een groep.
- Bepaalde draaiingen en translaties vormen een groep, die toepassing vindt in de leer van de symmetrie, bijvoorbeeld translatiesymmetrie. Continue symmetrieën, zoals rotatiesymmetrie, worden door lie-groepen gemodelleerd.
Voorbeeld 1, gehele getallen[bewerken | brontekst bewerken]
Een van de bekendste groepen is de verzameling van gehele getallen , die bestaat uit de getallen
De optelling van de gehele getallen heeft de volgende eigenschappen, die dienen als een model voor de abstracte groepsaxioma's die in de onderstaande definitie worden gegeven.
- Voor elke twee gehele getallen en is de som ook een geheel getal. Met andere woorden, het proces van het bij elkaar optellen van twee gehele getallen heeft als resultaat weer een geheel getal. De gehele getallen zijn gesloten onder de operatie optellen.
- Voor alle gehele getallen en is . Eerst bij opgetellen en dan het resultaat hiervan bij opgetellen, geeft hetzelfde eindresultaat als het optellen van bij de som van en . Optellen is een associatieve bewerking.
- Voor elk geheel getal is . Het getal nul gedraagt zich neutraal ten opzichte van de optelling. Het wordt het neutrale element van de operatie optelling genoemd, of algemeen het identiteitselement, omdat het optellen van nul bij een willekeurig geheel getal ditzelfde gehele getal als resultaat oplevert.
- Voor elk geheel getal is er een geheel getal , zodanig dat . Het gehele getal wordt het inverse element van het gehele getal genoemd en gewoonlijk aangeduid door , door min a.
Voorbeeld 2, permutatiegroepen[bewerken | brontekst bewerken]
De groep van alle permutaties van een rij van elementen heet de symmetrische groep . De naam van deze groep is niet aan de symmetrie in de groep ontleend.
Voorbeeld 3, dihedrale groep[bewerken | brontekst bewerken]
De symmetrieën, dat wil zeggen rotaties en spiegelingen, van een vierkant vormen een groep die de dihedrale groep wordt genoemd.[21] De dihedrale groep kent de onderstaande acht symmetrieën:
- * de identieke afbeelding, die alles onveranderd laat, aangeduid door id;
- * rotaties van het vierkant 90° right, 180° right en 270° met de klok mee, aangeduid door respectievelijk en ;
- * spiegelingen over de verticale en horizontale middellijn ( en ) of door de twee diagonalen ( en ).
Elke twee symmetrieën en kunnen worden samengesteld, dat wil zeggen, de een na de ander toegepast. Het resultaat van eerst uitvoeren en dan wordt symbolisch van rechts naar links geschreven als ("pas de symmetrie toe, na eerst de symmetrie uitgevoerd te hebben". De van "rechts-naar-links" notatie komt voort uit de samenstelling van functies). De groepstabel aan de rechterkant geeft de resultaten van alle mogelijke samenstelling van symmetrieën. De 270° rotatie met de klok mee () en vervolgens horizontaal omkeren () is hetzelfde als het uitvoeren van een spiegeling over de diagonaal (). Door gebruik te maken van de bovengenoemde symbolen, die in het blauw in de groepstabel zijn weergegeven:
| • | ||||||||
|---|---|---|---|---|---|---|---|---|
| id | ||||||||
| De elementen en vormen een ondergroep, die in het roze (bovenkant links) is aangegeven. Een linker en rechter nevenklasse van deze ondergroep is respectievelijk in het groen (in de laatste rij) en in het geel (de laatste kolom) aangegeven. | ||||||||
Gezien deze verzameling van symmetrieën en de beschreven operatie, kunnen de groepsaxioma's als volgt worden opgevat:
- Het axioma van geslotenheid vraagt dat de compositie van twee symmetrieën en ook een symmetrie is. Een ander voorbeeld voor de groepsoperatie is
- ,
- dat wil zeggen een rotatie van 270° met de klok mee na het vierkant eerst diagonaal geflipt te hebben over de tegendiagonaal (). Inderdaad geeft elke andere combinatie van twee symmetrieën opnieuw een symmetrie. Hier kan men zich zelf van overtuigen door dit voor elke samenstelling te controleren in de groepstabel.
- De associativiteitsrestrictie heeft betrekking op het samenstellen van meer dan twee symmetrieën: gegeven drie elementen , en van , zijn er twee mogelijke manieren om " dan dan " te berekenen. Het vereiste dat
- betekent dat de samenstelling van de drie elementen onafhankelijk is van de prioriteit van de operaties, dat wil zeggen het samenstellen van eerst uitvoeren en vervolgens na op het resultaat van , op hetzelfde neerkomt als uitvoeren na de compositie van en . Men kan bijvoorbeeld controleren dat door gebruik te maken van de groepstabel aan de rechterkant
- , wat gelijk is aan
- Het identiteitselement is de symmetrie , die alles ongewijzigd laat: voor elke symmetrie is uitvoeren na , of na , gelijk aan alleen uitvoeren. In symbolische vorm,
- ,
- De inverse van een element maakt de transformatie van dat element ongedaan. Elke symmetrie kan ongedaan worden gemaakt. De identiteit , de flips en de rotatie over 180° zijn hun eigen inverse, omdat deze operaties twee keer achter elkaar uitvoeren het vierkant teruggeeft met de originele oriëntatie. De rotaties en zijn elkaars inverse, omdat rotatie over eenbepaalde hoek, en vervolgens over dezelfde hoek de andere kant op roteren, het vierkant ongewijzigd laat. In symbolen,
In contrast met de groep van de gehele getallen zoals hierboven besproken, waar de volgorde van de operatie niet relevant is, is dit in D4 wel van belang, bijvoorbeeld:
- ,
maar
Met andere woorden: is geen abelse groep. Dit maakt de groepsstructuur moeilijker dan bij de eerder geïntroduceerde groep van gehele getallen.
Notatie[bewerken | brontekst bewerken]
Voor de groepsbewerking maakt men gewoonlijk gebruik van de multiplicatieve notatie:
- In plaats van noteert men: of simpelweg , en noemt dit het product van en .
- Het neutraal element wordt als 1 of als genoteerd.
- De inverse van een element wordt genoteerd als .
Indien de bewerking commutatief is, wordt in veel gevallen gebruikgemaakt van de additieve notatie:
- In plaats van noteert men: , en noemt dit de som van en .
- Het neutraal element wordt als 0 genoteerd.
- De inverse van een element wordt genoteerd als en aangeduid als de tegengestelde van .
- wordt ook genoteerd als .
Eenvoudige eigenschappen[bewerken | brontekst bewerken]
Basisfeiten over alle groepen die direct uit de groepaxioma's kunnen worden verkregen, worden meestal ondergebracht onder de elementaire groepentheorie.[22]
Twee belangrijke gevolgen van de groepsaxioma's zijn dat in een groep precies één identiteitselement voorkomt en dat ieder element precies één invers element heeft. Het is daarom gebruikelijk om te spreken van het identiteitselement en de inverse van een element.[23]
Puntsgewijs opgesomd gelden de volgende eenvoudige eigenschappen:
- Een groep heeft precies één neutraal element.
- Elk element heeft precies één inverse.
- De inverse van een product is gelijk aan het product van de inversen in omgekeerde volgorde, dat wil zeggen: .
- Herhaalde bewerking kan genoteerd worden zonder haakjes. Wegens de associativiteit is de uitdrukking ondubbelzinnig.
Bewijs van de uniciteit van het neutrale element[bewerken | brontekst bewerken]
Stel dat ook neutraal element is. Dan is:
- ,
maar omdat e zelf neutraal element is geldt ook:
- ,
Gevolg:
- .
Bewijs van de uniciteit van de inverse[bewerken | brontekst bewerken]
Stel zijn beide inversen van . Dan is:
- ,
dus
- .
Blijkbaar heeft slechts één unieke inverse.
Uit de uniciteit van de inverse volgt:
en
- .
Implicatie van de associativiteitseigenschap[bewerken | brontekst bewerken]
Herhaaldelijk toepassen van het axioma, dat de bewerking in de groep associatief is, laat zien dat de eenduidigheid van
in het algemeen ook geldt wanneer er meer dan drie elementen staan. Omdat dit impliceert dat haakjes overal binnen een dergelijke reeks van termen kunnen worden ingevoegd, worden haakjes meestal weggelaten[24].
Deling[bewerken | brontekst bewerken]
In een groep is het mogelijk een deling uit te voeren. Bij gegeven elementen en van de groep bestaat er precies één oplossing van de vergelijking [23]. Door rechtsvermenigvuldiging met volgt de oplossing . Op gelijke wijze is er precies één oplossing van de vergelijking , namelijk . In het algemeen komen en niet met elkaar overeen.
Afzwakking van de groepsaxioma's[bewerken | brontekst bewerken]
De axioma's kunnen worden afgezwakt door alleen het bestaan van een linkseenheid te eisen en voor ieder element slechts het bestaan van een linksinverse. In dat geval kan namelijk alsnog worden aangetoond[25] dat de inverse in feite tweezijdig is. Als namelijk een linksinverse van is, dus , geldt
-
- ,
waaruit blijkt dat ook de rechtsinverse van is.
Verder geldt voor de linkseenheid dat voor alle geldt: . Vanzelf is dan ook rechtseenheid, want voor alle is:
- ,
want eerder bleek dat ook rechtsinverse is, dus:
Basisconcepten[bewerken | brontekst bewerken]
Om groepen op een niveau te begrijpen dat verdergaat dan louter symbolische manipulatie, moeten meer structurele concepten worden ingezet. Er is een conceptueel uitgangspunt dat ten grondslag ligt aan al de volgende begrippen: om te profiteren van de structuur die door groepen wordt geboden, een structuur die niet aanwezig is in "structuurloze" verzamelingen, moeten aan groepen gerelateerde constructies verenigbaar zijn met de groepsbewerking. Deze compatibiliteit manifesteert zichzelf op verschillende manieren in de volgende begrippen. Men kan bijvoorbeeld groepen aan elkaar relateren met behulp van functies die groepshomomorfismen worden genoemd. Door het genoemde principe zijn ze verplicht om de groepsstructuren in een precieze betekenis te respecteren. De structuur van de groepen kan ook worden begrepen door groepen in stukken op te breken. Deze stukken noemt men deelgroepen en quotiëntgroepen. Het principe van het "behoud van structuur" - een terugkerend onderwerp door de hele wiskunde - is een instantie van werken met een categorie, in dit geval de categorie van groepen.
Isomorfie[bewerken | brontekst bewerken]
Twee groepen worden isomorf genoemd als er een groepsisomorfisme tussen hen bestaat. Isomorfe groepen hebben in feite dezelfde structuur.
Ondergroepen[bewerken | brontekst bewerken]
Een deelverzameling van een groep die met dezezelfde groepsbewerking een groep vormt, heet een ondergroep van .[26]
Nevenklassen[bewerken | brontekst bewerken]
Een ondergroep van een groep induceert een equivalentierelatie op , door:
- als er een is zodat .
De equivalentieklassen worden de linkernevenklassen van genoemd. Het zijn de deelverzamelingen .[27].
Op soortgelijke wijze zijn ook rechternevenklassen gedefinieerd.
Door de nevenklassen te beschouwen wordt afgezien van de werking van de elementen in de betrokken ondergroep.
Factorgroepen[bewerken | brontekst bewerken]
Als een ondergroep een normaaldeler is, kan het negeren van de interne structuur van die ondergroep door haar nevenklassen in beschouwing te nemen, gestructureerd worden als groep, de zogeheten factorgroep of quotiëntgroep, genoteerd als .[28]
Een normaaldeler of normale ondergroep, van een groep is een ondergroep met de eigenschap dat voor alle en geldt: .
- Voorbeeld
| • | R | U |
|---|---|---|
| R | R | U |
| U | U | R |
| Groepstabel van de factorgroep . | ||
De ondergroep van die bestaat uit de rotaties is een normaaldeler. De factorgroep bestaat uit twee elementen, en wel zelf, die het identiteitselement voorstelt en . De groepsbewerking op het quotiënt is weergegeven in de nevenstaande tabel. Zo is bijvoorbeeld:
Zowel de ondergroep als de bijbehorende quotiëntgroep zijn abels, hoewel zelf niet abels is.
Voorbeelden[bewerken | brontekst bewerken]

Voorbeelden en toepassingen van groepen zijn er in overvloed. Een startpunt is de hierboven geïntroduceerde groep Z van de gehele getallen met optelling als groepsbewerking. Als men in plaats van optelling vermenigvuldigen als groepsbewerking neemt, verkrijgt men multiplicatieve groepen. Deze multiplicatieve groepen zijn voorlopers van belangrijke constructies in de abstracte algebra.
Ook in vele andere wiskundige deelgebieden maakt men gebruik van groepen. Wiskundige objecten worden vaak onderzocht door groepen met deze objecten te associëren en vervolgens de eigenschappen van de corresponderende groepen te bestuderen. Henri Poincaré kwam bijvoorbeeld op het spoor van wat nu de algebraïsche topologie wordt genoemd, door de invoering van de fundamentaalgroep[29]. Door het leggen van deze verbinding konden topologische eigenschappen, zoals nabijheid en continuïteit vertaald worden in eigenschappen van groepen. Elementen van de fundamentaalgroep worden bijvoorbeeld weergegeven door lussen. Het onderste plaatje aan de rechterkant laat enkele lussen in een vlak minus een punt zien. De blauwe lus wordt als nul-homotoop (en dus niet relevant) gezien, dit omdat deze lus continu tot een punt kan slinken. De aanwezigheid van het gat voorkomt echter dat de oranje lus ook tot een punt kan worden geslonken. De fundamentaalgroep van het vlak, waaruit een punt is verwijderd, blijkt, gegenereerd door de oranje lus (of enige andere lus die zich eenmaal rondom het gat windt), oneindig cyclisch te zijn. Op deze manier detecteert de fundamentaalgroep het gat.
In recentere toepassingen werkt deze invloed ook omgekeerd. Men bestudeert nu meetkundige constructies die worden onderbouwd door een groeptheoretische achtergrond. In dezelfde geest maakt de meetkundige groepentheorie gebruik van meetkundige concepten, bijvoorbeeld in de studie van hyperbolische groepen.[30] Andere deelgebieden, waar groepen een cruciale rol spelen zijn de algebraïsche meetkunde en de getaltheorie.[31].
Naast de bovengenoemde theoretische toepassingen, bestaan er vele praktische toepassingen van groepen. Cryptografie bijvoorbeeld berust op een benadering gebaseerd op de abstracte groepentheorie, samen met algoritmische kennis, verkregen uit de computationele groepentheorie, in het bijzonder wanneer deze wordt geïmplementeerd voor eindige groepen[32]. Toepassingen van de groepentheorie beperken zich niet tot de wiskunde, ook de natuurwetenschappen, zoals de natuurkunde, de scheikunde en de informatica profiteren van het concept.
Getallen[bewerken | brontekst bewerken]
Veel getalsystemen, zoals die van de gehele - en de rationale getallen beschikken over een natuurlijk gegeven groepsstructuur. In sommige gevallen, zoals bij de rationale getallen, leiden zowel de operaties optellen en vermenigvuldigen tot een groepsstructuur. Dergelijke getalsystemen zijn voorlopers van meer algemene algebraïsche structuren die bekendstaan als ringen en velden. Verdere abstract algebraïsche concepten, zoals modulen, vectorruimten en algebra's vormen ook groepen.
Gehele getallen[bewerken | brontekst bewerken]
De groep van gehele getallen onder de optelling, aangeduid met , is hierboven beschreven. De gehele getallen, met in plaats daarvan de operatie van vermenigvuldiging in plaats van optellen, , vormt geen groep. Aan de groepsaxioma's van geslotenheid, associativiteit en identiteit wordt voldaan, maar er bestaat geen inverse. De enige oplossing van bijvoorbeeld de vergelijking is , en dat is geen geheel getal. Dus heeft niet elk element van een (multiplicatieve) inverse.
Rationale getallen[bewerken | brontekst bewerken]
Breuken van gehele getallen, met , staan bekend als rationale getallen . Onder de optelling is een groep. Omdat het getal 0 geen multiplicatieve inverse heeft vormen de rationale getallen geen groep onder de vermenigvuldiging. Laat men de 0 weg, dan is er geen probleem: is een abelse groep.
De verwevenheid van de groepsbewerkingen optellen en vermenigvuldigen levert ingewikkeldere wiskundige structuren op die ringen worden genoemd en waarbij deling mogelijk is.
Modulair rekenen[bewerken | brontekst bewerken]
Voor elk priemgetal , levert modulair rekenen de multiplicatieve groep van gehele getallen modulo .[33] Haar elementen zijn gehele getallen die niet deelbaar zijn door , modulo p, dat wil zeggen dat twee getallen als gelijkwaardig worden beschouwd, indien hun verschil deelbaar is door . Deze groepen zijn van cruciaal belang voor de publieke sleutelcryptografie.
Cyclische groepen[bewerken | brontekst bewerken]
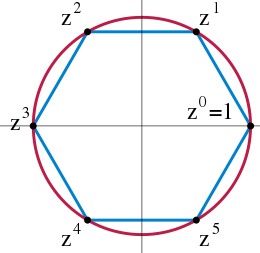
Een cyclische groep is een groep die wordt voortgebracht door één enkel element. Als de groepsbewerking als vermenigvuldiging wordt beschouwd, zijn alle elementen machten, zowel positieve als negatieve, van het voorbrengende element.[34]. Is een voortbrengend element dan bestaat de groep uit . Een cyclische groep van eindige orde bestaat uit . Dit verklaart ook de term 'cyclisch'. Sommige cyclische groepen hebben, ondanks de naam "cyclische groep", een oneindig aantal elementen. In deze groepen zijn voor elk element ongelijk aan het neutrale element, alle machten van van elkaar verschillend. Een oneindige cyclische groep is isomorf met , de groep van de gehele getallen onder optelling[35]. Aangezien deze groep abels is, is elke oneindige cyclische groep dit ook.
Symmetriegroepen[bewerken | brontekst bewerken]

Symmetriegroepen zijn groepen die bestaan uit symmetrieën van gegeven wiskundige objecten - al of niet van meetkundige aard, zoals de symmetriegroep van het vierkant of van algebraïsche aard, zoals veeltermvergelijkingen en hun oplossingen[36]. In conceptuele zin kan groepentheorie worden opgevat als de studie van symmetrie. In de wiskunde vereenvoudigden symmetrieën de studie van meetkundige of analytische objecten aanzienlijk. Van een groep zegt men dat deze op een ander wiskundig object X inwerkt, als er voor elk groepselement in overeenstemming met de groepswetten een bijbehorende bijectie van X is. In de illustratie links werkt een element van orde 7 van de (2,3,7) driehoeksgroep in op de betegeling door de gemarkeerde verwrongen driehoeken (en de anderen ook) te verwisselen. Door een groepsbewerking raakt het groepspatroon verbonden met de structuur van het object, waarop de groep inwerkt.
In scheikundige deelgebieden, zoals de kristallografie, beschrijven ruimte- en puntgroepen moleculaire- en kristalsymmetrieën. Deze symmetrieën liggen ten grondslag aan het scheikundige en natuurkundige gedrag van deze systemen. De groepentheorie vereenvoudigt de kwantummechanische analyse van deze eigenschappen[37]. Groepentheorie wordt bijvoorbeeld gebruikt om aan te tonen dat optische overgangen tussen bepaalde kwantumniveaus niet kunnen optreden, simpelweg omdat de symmetrie van de betrokken toestanden dit niet toestaat.
Niet alleen zijn groepen nuttig om de implicaties van symmetrieën in moleculen te beoordelen, maar verrassend genoeg voorspellen zij ook dat moleculen soms hun symmetrie kunnen veranderen. Het Jahn-Teller-effect is een vervorming van een molecuul van hoge symmetrie, wanneer deze molecule een bepaalde grondtoestand van lagere symmetrie aanneemt uit een verzameling van mogelijke grondtoestanden, die aan elkaar zijn gerelateerd door de symmetrie-operaties van dit molecuul.[38][39]
Op gelijkaardige wijze helpt de groepentheorie veranderingen in de natuurkundige eigenschappen te voorspellen, die plaatsvinden wanneer een materiaal een faseovergang ondergaat, bijvoorbeeld van een kubische naar een tetrahedrale kristallijne vorm. Een voorbeeld hiervan zijn ferro-elektrische materialen, waar de verandering van een para-elektrische naar een ferro-elektrische toestand optreedt bij de Curie-temperatuur. Deze verandering is gerelateerd aan een verandering van de hoger-symmetrische para-elektrische toestand naar de lager-symmetrische ferro-elektrische toestand. Dit gaat vergezeld door een zogenoemde zachte fonon modus, een vibrationeel roostermodus, die bij de faseovergang naar een nulfrequentie gaat[40].
Zulke spontane symmetriebreking heeft verdere toepassing gevonden in de elementaire deeltjesfysica, waar haar voorkomen is gerelateerd aan de verschijning van Goldstone-bosonen.
Eindige symmetriegroepen, zoals de Mathieu-groepen worden gebruikt in de codeertheorie, die op zijn beurt wordt toegepast in foutcorrectie algoritmen voor verzonden data en in cd-spelers[41]. Een andere toepassing is de differentiaal Galois-theorie, die functies karakteriseert, die antiafgeleiden van een voorgeschreven vorm hebben, en die daardoor groep-theoretische criteria geeft wanneer oplossingen van bepaalde differentiaalvergelijkingen zich al of niet goed-gedragen. Meetkundige eigenschappen, die stabiel blijven onder groepsbewerkingen, worden onderzocht in de meetkundige invariantentheorie[42]
Symmetrie[bewerken | brontekst bewerken]
Iedere groep heeft een bepaalde symmetrie. Dat betekent dat bij twee geconjugeerde elementen en van de groep een permutatie van bestaat die op afbeeldt, zodanig dat en isomorf zijn. Op die manier is symmetrisch.
Euclidische groepen[bewerken | brontekst bewerken]
De euclidische groep is de symmetriegroep van de -dimensionale euclidische ruimte. De elementen van de euclidische groep zijn de isometrieën van de euclidische ruimte. Ze zijn van de vorm met een orthogonale matrix, dat wil zeggen .
Algemene lineaire groepen en representatietheorie[bewerken | brontekst bewerken]

Matrixgroepen bestaan uit matrices samen met de operatie matrixvermenigvuldiging. De algemene lineaire groep bestaat uit alle reële inverteerbare -matrices.[43] Ondergroepen van een algemene lineaire groep noemt men matrixgroepen of lineaire groepen. Het hierboven genoemde voorbeeld van een tweevlakshoekgroep kan gezien worden als een (zeer kleine) matrixgroep. Een andere belangrijke matrixgroep is de speciale orthogonale groep . Deze groep beschrijft alle mogelijke rotaties in dimensies. Via Euler-hoeken worden rotatiematrices gebruikt in de computergraphics.[44]
Representatietheorie is zowel een toepassing van het begrip groep alsook belangrijk voor een dieper begrip van groepen.[45][46] De theoie bestudeert een groep door haar groepsbewerkingen op andere ruimten te bestuderen. Een brede klasse van groepsrepresentaties zijn lineaire representaties, dat wil zeggen dat de groep inwerkt op een vectorruimte, zoals de driedimensionale Euclidische ruimte . Een representatie van op een -dimensionale reële vectorruimte is een groepshomomorfisme
- .
van de groep naar de algemene lineaire groep. Op deze manier vertaalt de groepsbewerking, die ook abstract kan zijn gegeven, naar de vermenigvuldiging van matrices, waardoor deze toegankelijk wordt voor expliciete berekeningen.
Gegeven een groepsbewerking, geeft dit extra middelen om de wiskundige objecten, waarop de groep inwerkt, te bestuderen. Aan de andere kant levert het ook informatie over de groep op. Groepsrepresentatie is een ordenend principe in de theorie van de eindige groepen, de Lie-groepen, de algebraïsche groepen en de topologische groepen, vooral (lokaal) compacte groepen[45][47].
Galoisgroepen[bewerken | brontekst bewerken]
Galoisgroepen zijn ontwikkeld om veeltermvergelijkingen te helpen oplossen door hun symmetrie-eigenschappen in beschouwing te nemen.[48][49] De oplossingen van bijvoorbeeld de vierkantsvergelijking worden gegeven door
- .
Het verwisselen van "+" en "-" in deze uitdrukking, waardoor de twee oplossingen van de vergelijking worden verwisseld, kan als een (eenvoudige) groepsoperatie worden gezien.
Voor derdegraads- en vierdegraadsvergelijkingen zijn vergelijkbare formules bekend, maar deze bestaan in het algemeen niet voor vijfdegraadsvergelijkingen en hoger.[50] Abstracte eigenschappen van Galoisgroepen geassocieerd met veeltermen (met name hun oplosbaarheid) geven een criterium voor veeltermen, waarvan alle oplossingen uit te drukken zijn door radicalen, dat wil zeggen oplossingen die zijn uit te drukken in een vorm, waarbij uitsluitend gebruik wordt gemaakt van optelling, vermenigvuldigen, en wortels, vergelijkbaar met de formule hierboven.[51]
Dit probleem kan worden aangepakt door een verschuiving naar veldtheorie, waarbij men het splitsingsveld van een polynoom in beschouwing neemt. Moderne Galoistheorie veralgemeent het bovenstaande type Galoisgroepen van velduitbreidingen en legt, door middel van de hoofdstelling van de Galoistheorie, een precieze relatie tussen de velden en groepen vast, daarmee nogmaals de alomtegenwoordigheid van groepen in de wiskunde onderstrepend.
Eindige groepen[bewerken | brontekst bewerken]
Een groep met een eindig aantal elementen wordt eindig genoemd. Het aantal elementen heet de orde van de groep[52]. Een belangrijke klasse vormen de symmetrische groepen , de groepen van permutaties van verschillende letters, en alle ondergroepen daarvan. De symmetrische groep op drie letters bijvoorbeeld bestaat uit alle mogelijke verwisselingen van de drie letters ABC, dat wil zeggen bevat de elementen ABC, ACB, ..., tot CBA, in totaal 6 (3 faculteit) elementen. Deze klasse is van fundamenteel belang, aangezien volgens de stelling van Cayley iedere eindige groep kan worden uitgedrukt als een ondergroep van een symmetrische groep .
De orde van een element in een groep is het kleinste positieve gehele getal waarvoor .[53] De orde van een element is gelijk aan de orde van de cyclische ondergroep die door dit element wordt gegenereerd.
De dihedrale groep Dih4 is een eindige groep van orde 8. De orde van is 4, evenals de orde van de ondergroep die de groep genereert. De orde van de reflectie elementen is 2. Beide orden zijn delers van 8, zoals voorspeld door de stelling van Lagrange.
Het aantal van de symmetrische groep zelf, maar ook van alle ondergroepen ervan, gezien als permutatiegroepen van letters, groeit voor snel. Er is een lijst van kleine groepen, dus van de eerste eindige groepen.
Classificatie van eindige enkelvoudige groepen[bewerken | brontekst bewerken]
Het streven naar een volledige indeling (of lijst) van alle eindige groepen leidt al snel tot moeilijke en diepe wiskunde. Een dergelijke indeling is volgens de classificatiestelling mogelijk. Als gevolg van de stelling van Lagrange zijn eindige groepen van orde een priemgetal , noodzakelijkerwijs cyclische, dus abelse groepen, isomorf met . Van groepen van orde kan men aantonen dat zij abels zijn, een stelling die niet meer geldt voor groepen van orde , zoals de niet-abelse groep van orde 8 = 23 hierboven aantoont.[54][55]
Computeralgebrasystemen kunnen worden gebruikt voor de lijst van kleine groepen, maar er is geen classificatie voor alle eindige groepen. Een tussentijdse stap is de classificatie van alle eindige enkelvoudige groepen. Een niet-triviale groep wordt enkelvoudig genoemd als zijn enige normaaldelers de triviale groep en de groep zelf zijn. De stelling van Jordan-Hölder gebruikt eindige enkelvoudige groepen als de bouwstenen voor alle eindige groepen.[56]
De classificatie van alle eindige enkelvoudige groepen was een belangrijke prestatie in de hedendaagse groepentheorie. De winnaar van de Fieldsmedaille in 1998, Richard Borcherds slaagde erin om een verrassend en diep verband te bewijzen tussen de monstergroep, de grootste eindige enkelvoudige sporadische groep, tussen zekere modulaire functies, die een onderdeel vormen van de complexe functietheorie, en de snaartheorie. Deze laatste theorie wordt geacht de beschrijving van een groot aantal natuurkundige verschijnselen in zich te verenigen.[57] Voordat het verband door Borcherds werd bewezen, werd het het vermoeden van de monsterlijke maneschijn genoemd.
Hogere groepentheorie[bewerken | brontekst bewerken]
Het enumeratieprobleem voor eindige groepen is herleidbaar tot het enumeratieprobleem van eindige enkelvoudige groepen.
Een eindige enkelvoudige groep behoort tot een van de volgende 5 families van groepen:
- Cyclische groepen
- Alternerende groepen
- Chevalley-groepen
- Eindige groepen van Lie-type, niet te verwarren met Lie-groepen
- De lijst der 26 Sporadische groepen
Alleen het aantal sporadische groepen is eindig.
Groepen met additionele structuur[bewerken | brontekst bewerken]
Veel groepen zijn tegelijkertijd groepen en voorbeelden van andere wiskundige structuren. In de taal van de categorietheorie zijn ze groepsobjecten in een categorie, wat betekent dat ze objecten zijn (dat wil zeggen, voorbeelden van een andere wiskundige structuur) die verschijnen met transformaties (morfismen genoemd), die de groepsaxioma's nabootsen. Elke groep, zoals hierboven gedefinieerd, is bijvoorbeeld ook een verzameling, een groep is dus een groepsobject in de categorie van verzamelingen, Set.
Topologische groepen[bewerken | brontekst bewerken]
Sommige topologische ruimten kunnen zijn uitgerust met een groepswet. Om de groepswet en de topologie goed met elkaar te verweven, moeten de groepsbewerkingen continue functies zijn, dat wil zeggen dat en niet wild mogen variëren als en slechts een klein beetje verschillen. Dergelijke groepen worden topologische groepen genoemd. Zij zijn de groepsobjecten in de categorie van topologische ruimten[58] De elementairste voorbeelden zijn de reële getallen onder optelling, , en op soortgelijke wijze enig ander topologisch veld, zoals de complexe- of de -adische getallen. Al deze groepen zijn lokaal compact en hebben dus Haar-maten en kunnen bestudeerd worden met behulp van de harmonische analyse.
De eerdere biedt een abstract formalisme van invariante integralen. In het geval van reële getallen betekent invariantie bijvoorbeeld:
voor elke constante . Matrixgroepen over deze velden vallen onder dit regime, net zoals adele-ringen en adelische algebraïsche groepen, beide begrippen die fundamenteel zijn in de getaltheorie[59]. Galoisgroepen van oneindige velduitbreidingen, zoals de absolute Galoisgroep, kunnen ook worden uitgerust met een topologie, de zogenaamde Krull-topologie. Deze is op zijn beurt centraal in de veralgemening van de hierboven geschetste aansluiting van velden en groepen tot oneindige velduitbreidingen[60]. Een geavanceerde veralgemening van dit idee, aangepast aan de behoeften van de algebraïsche meetkunde, is de étale fundamentaalgroep.[61]
Lie-groepen[bewerken | brontekst bewerken]
Lie-groepen, zo genoemd ter ere van de Noorse wiskundige Sophus Lie, zijn groepen die ook een variëteitsstructuur hebben, dat wil zeggen dat het ruimten zijn, die er lokaal uitzien als een Euclidische ruimte van de geëigende dimensie[62] Ook hier moet de additionele structuur, hier de variëteitsstructuur, verenigbaar zijn, dat wil zeggen dat de afbeeldingen die corresponderen met vermenigvuldiging en de inverse glad moeten zijn.
Een standaard voorbeeld is de hierboven geïntroduceerde algemene lineaire groep: het is een open deelverzameling van de ruimte van alle -matrices, omdat hij wordt gegeven door de ongelijkheid
- ,
waarin een -matrix is[63].
Lie-groepen zijn van fundamenteel belang in de natuurkunde: de stelling van Noether verbindt continue symmetrieën met de behoudswetten[64]. Zowel rotatie als translatie in ruimte en tijd zijn fundamentele symmetrieën van de wetten van de mechanica. Zij kunnen bijvoorbeeld worden gebruikt om eenvoudige modellen te construeren - waarbij bijvoorbeeld axiale symmetrie aan een situatie wordt opgelegd, wat doorgaans zal leiden tot een aanzienlijke vereenvoudiging van de vergelijkingen, die men moet oplossen om een natuurkundige beschrijving te geven. Een ander voorbeeld zijn de Lorentz-transformaties, die metingen van tijd en snelheid van twee ten opzichte van elkaar in beweging zijnde waarnemers aan elkaar relateert. Ze kunnen worden gededuceerd op een zuiver groepstheoretische manier, door de transformaties uit te drukken als een draaisymmetrie van de Minkowski-ruimte. Deze Minkowski-ruimte fungeert - in geval van significante zwaartekracht - als een model van de ruimtetijd in de speciale relativiteitstheorie.[65] De volledige symmetriegroep van de Minkowski-ruimte, dat wil zeggen inclusief translaties, staat bekend als de Poincaré-groep. Door het bovenstaande speelt deze een centrale rol in de speciale relativiteitstheorie en, bij implicatie, voor de kwantumveldentheorieën[66]. Symmetrieën die per locatie variëren staan centraal in de moderne beschrijving van de fysieke interacties met behulp van ijktheorieën[67].
Generalisaties[bewerken | brontekst bewerken]
In de abstracte algebra kunnen meer algemene wiskundige structuren worden gedefinieerd door een aantal van de groepsaxioma's, die een groep definiëren, af te zwakken[68][69][70]. Als men bijvoorbeeld de eis, dat elk element een inverse moet hebben, laat vallen, wordt de dan resulterende algebraïsche structuur een monoïde genoemd. De natuurlijke getallen (inclusief 0) vormen voor de groepsbewerking optelling een monoïde, net als de gehele getallen ongelijk aan 0 doen onder de groepsbewerking vermenigvuldiging , zie hierboven. Er is een algemene methode om op formele wijze inversen van elementen op te tellen bij elke (abelse) monoïde, bijna op dezelfde manier als wordt afgeleid van . Het resultaat van deze formele methode staat bekend als de Grothendieck-groep.
Groepoïden zijn vergelijkbaar met groepen, behalve dat de groepsbewerking niet hoeft te worden gedefinieerd voor alle en . Zij ontstaan in de studie van meer ingewikkelde vormen van symmetrie, vaak in topologische en analytische structuren, zoals de fundamentele groupoïde. Ten slotte is het mogelijk om elk van deze concepten te generaliseren door de binaire operatie te vervangen door een operatie met een willekeurige ariteit , dat wil zeggen een operatie waarbij argumenten in het spel zijn. Met de juiste generalisatie van de groepsaxioma's geeft dit aanleiding tot een groep met ariteit .[71]
Voetnoten[bewerken | brontekst bewerken]
- ↑ Herstein, 1975, § 2, blz. 26
- ↑ Hall, 1967, §1.1, blz. 1" "Het idee van een groep is er een dat de gehele zuivere en toegepaste wiskunde doordringt."
- ↑ Wussing, 2007
- ↑ Kleiner, 1986
- ↑ Smith, 1906
- ↑ Galois, 1908
- ↑ Kleiner, 1986, p. 202
- ↑ Cayley, 1889
- ↑ Wussing, 2007, § III.2
- ↑ Lie, 1973
- ↑ Kleiner, 1986, pag. 204
- ↑ Wussing, 2007, § I.3.4
- ↑ Jordan, 1870
- ↑ von Dyck, 1882
- ↑ Curtis, 2003
- ↑ Mackey, 1976
- ↑ Borel, 2001
- ↑ Aschbacher, 2004
- ↑ Herstein, 1975, §2.1, pag. 27
- ↑ Lang, 2005, App. 2, p. 360
- ↑ Herstein, 1975, §2.6, pag. 54
- ↑ Ledermann, 1953, §1.2, pag. 4-5
- ↑ a b Lang, 2005, §II.1, blz. 17
- ↑ Ledermann, 1973, §I.1, blz. 3
- ↑ Lang, 2002, §I.2 blz. 7
- ↑ Lang, 2005, §II.1, blz. 19
- ↑ Lang, 2005, § II.4, blz. 41
- ↑ Lang, 2005, §II.4, blz. 45
- ↑ Hatcher, 2002, hoofdstuk I, blz. 30
- ↑ Coornaert, Delzant, Papadopoulos, 1990
- ↑ bijvoorbeeld klassegroepen en picard-groepen; zie Neukirch, 1999, in het bijzonder §§I.12 en I.13
- ↑ Seress, 1997
- ↑ Lang, 2005, hoofdstuk VII
- ↑ Lang, 2005, §II.1, p. 22
- ↑ Lang, 2005, §II.1, p. 22 (voorbeeld 11)
- ↑ Weyl, 1952
- ↑ Conway, Delgado Friedrichs, Huson, Thurston, 2001. Zie ook Bishop, 1993
- ↑ The Jahn-Teller Effect, Isaac Bersuker, pag 2, 0521822122, Cambridge University Press, 2006
- ↑ Jahn, Teller, 1937
- ↑ Structure and Dynamics: an atomic view of materials, Martin T Dove, pag 265, 0198506783, Oxford University Press, 2003
- ↑ Welsh, 1989
- ↑ Mumford, Fogarty, Kirwan, 1994
- ↑ Lay, 2003
- ↑ Kuipers, 1999
- ↑ a b Fulton, Harris, 1991
- ↑ Serre, 1977
- ↑ Rudin, 1990
- ↑ Robinson, 1996, loc = p. viii
- ↑ Artin, 1998
- ↑ Lang, 2002, Hoofdstuk VI (zie met name blz. 273 voor concrete voorbeelden)
- ↑ Lang, 2002, p. 292 (stelling VI.7.2
- ↑ Kurzweil, Stellmacher, 2004
- ↑ In oneindige groepen hoeft een dergelijke niet te bestaan, in welk geval men zegt dat de orde van oneindig is.
- ↑ Artin, 1991, stelling 6.1.14
- ↑ zie Lang, 2002, p. 77 voor soortgelijke resultaten
- ↑ Lang, 2002, § I.3, p.22
- ↑ Ronan, 2007
- ↑ Husain, 1966
- ↑ Neukirch, 1999
- ↑ Shatz, 1972
- ↑ Milne, 1980
- ↑ Warner, 1983
- ↑ Borel, 1991
- ↑ Goldstein,1980
- ↑ Weinberg, 1972
- ↑ Naber, 2003
- ↑ Becchi, 1997
- ↑ Mac Lane, 1998
- ↑ Denecke, Wismath, 2002
- ↑ Romanowska, Smith, 2002
- ↑ Dudek, 2001
Referenties[bewerken | brontekst bewerken]
Primaire referenties[bewerken | brontekst bewerken]
- (en) Artin, Michael, Algebra, Prentice Hall, 1991, isbn=978-0-89871-510-1, hoofdstuk 2 bevat een uiteenzetting op de bachelor van diverse in dit artikel besproken begrippen.
- (en) Devlin, Keith, The Language of Mathematics: Making the Invisible Visible, 2000, Owl Books, isbn=978-0-8050-7254-9, hoofdstuk 5 geeft een voor de leek toegankelijke uitleg van wat groepen precies zijn.
- (en) George G. Hall, Applied group theory, American Elsevier Publishing Co., Inc., 1967, New York, een elementaire inleiding.
- (en) Herstein, Israel Nathan, Abstract algebra, Prentice Hall Inc., Upper Saddle River, NJ, 3e editie, isbn=978-0-13-374562-7, 1996.
- (en) Herstein, Israel Nathan, Topics in algebra, Xerox College Publishing, Lexington, Mass. 2e editie, 1975.
- (en) Lang. Serge, Algebra, Graduate Texts in Mathematics, 211 (Revised 3e ed.), New York: Springer-Verlag, ISBN 978-0-387-95385-4, 2002.
- (en) Lang. Serge, Undergraduate Algebra, Springer-Verlag, Berlin, New York, 3e editie, isbn=978-0-387-22025-3, 2005.
- (en) Ledermann, Walter, Introduction to the theory of finite groups, Oliver and Boyd, Edinburgh and London, 1953.
- (en) Ledermann, Walter, Introduction to group theory, Barnes and Noble, New York, 1973.
- (en) Robinson, Derek John Scott, A course in the theory of groups, Springer-Verlag, Berlin, New York, 1996, isbn=978-0-387-94461-6.
Secundaire referenties[bewerken | brontekst bewerken]
- (en) Artin, Emil, Galois Theory, Dover Publications, New York, isbn=978-0-486-62342-9
- (en) Rudin, Walter, Fourier Analysis on Groups, Wiley-Blackwell, Wiley Classics, 1990, isbn=047152364X.
- (en) Weyl, Hermann, Symmetry, Princeton University Press, 1952, isbn=978-0-691-02374-8.

































































































































































