Wortel 2

De hypotenusa van een rechthoekige en gelijkbenige driehoek met rechthoekszijden 1 heeft de lengte √2

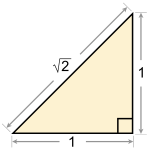
De wortel van (of uit) 2, geschreven als √2, is het positieve reële getal dat vermenigvuldigd met zichzelf gelijk is aan het getal 2:

${\sqrt {2}}>0$ en ${\sqrt {2}}\times {\sqrt {2}}=2$

√2 is een irrationaal getal dat bij benadering gelijk is aan:

1,414 213 562 373 095 048 801 688 724 209 698 078 569 671 875....

De breuk $99/70=1{,}4{\overline {142857}}$ (met overstreept repeterend deel) wordt als benadering van √2 gebruikt. Deze benadering is tot en met de vierde decimaal correct.

Volgens de definitie van gebroken machten kan ook geschreven worden: ${\sqrt {2}}=2^{\frac {1}{2}}$.

Geschiedenis

kleitablet YBC 7289, omstreeks 1800–1600 v.Chr.

Het Babylonische kleitablet YBC 7289 uit circa 1800-1600 v.Chr. geeft een benadering van √2 in vier sexagesimale cijfers, wat overeenkomt met ongeveer zes decimale cijfers

$1+{\frac {24}{60}}+{\frac {51}{60^{2}}}+{\frac {10}{60^{3}}}={\frac {30547}{21600}}=1{,}41421{\overline {296}}$

Waarbij het overstreepte gedeelte repeterend, repetent is.

Een andere precieze benadering van het getal wordt gegeven in oud-Indische wiskundige teksten, de Sulbasutras, van ongeveer 800-200 v.Chr: Verhoog de lengte [van de zijde] met zijn derde, en dit derde met zijn eigen vierde min het vierendertigste deel van dat vierde. Dat komt neer op,

$1+{\frac {1}{3}}+{\frac {1}{3\times 4}}-{\frac {1}{3\times 4\times 34}}={\frac {577}{408}}\approx 1{,}414215686$

Deze oude Indische benadering is de zevende in een reeks steeds nauwkeurigere benaderingen gebaseerd op de Pellreeks, die uit de kettingbreuk van √2 kan worden afgeleid.

Benaderingen

Irrationale getallen: ζ(3) √2 √3 √5 φ e π
Verschillende representaties van √2
binair	1,0110101000001001111...
decimaal	1,4142135623730950488...
hexadecimaal	1,6A09E667F3BCC908B2F...
kettingbreuk	$1+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+\ddots }}}}}}}}$

Er is een aantal algoritmes om ${\sqrt {2}}$ te benaderen als een breuk van gehele getallen of als decimaal getal. Het meest gebruikte algoritme hiervoor, dat ook veel in computers en rekenmachines wordt gebruikt, is de Babylonische methode om wortels uit te rekenen.

De methode gaat van de volgende gelijkheid uit:

${\sqrt {2}}={\frac {1}{2}}\left({\sqrt {2}}+{\frac {2}{\sqrt {2}}}\right)$

Met een startwaarde $a_{0}>0$, die een grove benadering van √2 is, wordt √2 daarna beter benaderd door de volgende iteratiestap uit te voeren:

$a_{n+1}={\frac {1}{2}}\left(a_{n}+{\frac {2}{a_{n}}}\right)={\frac {a_{n}}{2}}+{\frac {1}{a_{n}}}$

Als $a$ de limiet van dit proces is, geldt:

$a={\frac {a}{2}}+{\frac {1}{a}}$,

dus $a^{2}=2$.

Hoe meer wordt geïtereerd, hoe beter de benadering wordt. Elke iteratie verdubbelt het aantal correcte decimalen (kwadratische convergentie). Wordt begonnen met

$a_{0}=1$,

dan worden de volgende benaderingen (de correcte cijfers zijn onderstreept) in de reeks gegeven door:

$a_{1}=3/2={\underline {1}}{,}5$

$a_{2}=17/12={\underline {1{,}41}}6\ldots$

$a_{3}=577/408={\underline {1{,}41421}}5\ldots$

$a_{4}=665857/470832={\underline {1{,}41421356237}}46\ldots$

Deze methode werkt niet alleen voor twee, op deze manier kan de wortel van ieder getal, wanneer het tenminste positief is, worden bepaald.

De waarde van √2 is in 1997 door een team onder leiding van Yasumasa Kanada tot op 137.438.953.444 decimalen berekend. Deze precisie werd in februari 2006 overtroffen door Shigeru Kondo die op een 3,6 GHz PC met 16 GiB geheugen in iets meer dan 13 dagen en 14 uur 200 miljard, of 2 × 10¹¹, decimalen berekende.

De convergenten van de kettingbreuk zijn 1, 3/2, 7/5, 17/12, 41/29, ... (ze vormen een rij met lineaire convergentie). Ze vormen in bepaalde zin de beste benaderingen van √2 door breuken (niet te verwarren met de snelheid van convergentie van de rij):

• Voor elke convergent geldt dat de absolute waarde van de afwijking ten opzichte van √2 kleiner is dan bij elke andere breuk met een kleinere of gelijke noemer. Er zijn echter ook andere breuken met deze eigenschap, zoals 4/3 en 24/17.
• Zelfs de absolute waarde van de afwijking vermenigvuldigd met de noemer is kleiner dan bij elke andere breuk met een kleinere of gelijke noemer. Ook het omgekeerde geldt: elke breuk met deze eigenschap is een convergent van √2.

Irrationaal getal

De stelling dat √2 een irrationaal getal is, betekende de ontdekking van getallen die niet rationaal waren, dus niet als de breuk van twee natuurlijke getallen zijn te schrijven. Daarmee werd het wereldbeeld van de Pythagoreërs, die de natuurlijke getallen als de maat van alle dingen beschouwden, omver geworpen.

De stelling kan op diverse manieren worden bewezen, bijvoorbeeld met behulp van de hoofdstelling van de rekenkunde. Er staat in boek 10 van de Elementen van Euclides een bewijs door oneindige afdaling dat √2 geen rationaal getal kan zijn, maar er wordt sinds het begin van de 19e eeuw aangenomen dat het bewijs in de Elementen een interpolatie is.

Bewijs uit het ongerijmde 

Het is een bewijs uit het ongerijmde.

Stel dat √2 een rationaal getal is en wel ${\sqrt {2}}={\frac {a}{b}}$, waarin de breuk zodanig vereenvoudigd is dat $a$ en $b$ relatief priem zijn, geen factoren gemeenschappelijk hebben.

Dan volgt dat $b\,{\sqrt {2}}=a$ en na links en rechts kwadrateren dat $2b^{2}=a^{2}$.

Daaruit volgt dat $a^{2}$ een even getal is, dus ook dat $a$ zelf even is, zeg $a=2k$.

Daaruit volgt weer dat $2b^{2}=(2k)^{2}=4k^{2}$, dus is $b^{2}=2k^{2}$.

$b^{2}$ is kennelijk even, en daarmee ook $b$ zelf. Maar dat is in tegenspraak met het gegeven dat $a$ en $b$ relatief priem zijn. De veronderstelling dat √2 een rationaal getal is, heeft geleid tot een tegenspraak. Deze veronderstelling was dus onjuist en daarmee is bewezen dat √2 een irrationaal getal is.

Bewijs met behulp van de hoofdstelling van de rekenkunde 

Dit bewijs gaat ook uit het ongerijmde.

Veronderstel dat ${\sqrt {2}}$ een rationaal getal is en is te schrijven als het quotiént van twee positieve natuurlijke getallen $a$ en $b$: ${\frac {a}{b}}={\sqrt {2}}$.

Dan volgt na $b$ uit de noemer halen en na links en rechts kwadrateren dat $a^{2}=2b^{2}$.

Het aantal keer dat 2 in de ontbinding van $a^{2}$ en van $b^{2}$ voorkomt is even. Dan is vanwege de hoofdstelling van de rekenkunde, die zegt dat ieder gehele getal groter dan 1 op maar een manier in priemfactoren is te ontbinden, $a^{2}\neq 2b^{2}$, maar dat was de veronderstelling.

De veronderstelling dat ${\sqrt {2}}$ een rationaal getal is, was dus onjuist. Dat betekent dat ${\sqrt {2}}$ irrationaal is en de stelling is bewezen.

De A-standaard voor papierformaat

Zie Papierformaat voor het hoofdartikel over dit onderwerp.

De A-serie van papierformaten is een serie van vellen waarbij het volgende formaat steeds half zo groot is. De verhouding van de lange tot de korte zijde bedraagt steeds √2 : 1. De serie begint met A0, een vel met een oppervlakte van 1 m². Met de berekende verhouding levert dat een vel van 1189 mm bij 841 mm op.

Noten

Literatuur

• R. Bosch, P. Miedema (2019): Wortel 2 : Het verhaal van een opmerkelijk getal. Utrecht: Epsilon Uitgaven.
• (en) G Thomas: Realtime berekening van √2