Hoofdstelling van de integraalrekening
De hoofdstelling van de integraalrekening is een stelling uit de wiskunde die het verband geeft tussen de begrippen afgeleide en de integraal. Het is een centraal resultaat van de integraalrekening, of ruimer: de reële analyse, vandaar de naam. De stelling zegt dat differentiëren en integreren elkaars omgekeerde bewerkingen zijn. De concrete formulering en het bewijs hangt af van de gekozen definities en de gebruikte notie van integratie. In dit artikel wordt de meest elementaire notie van integreren gebruikt: de riemannintegraal.
Stelling[bewerken | brontekst bewerken]
De hoofdstelling van de integraalrekening bestaat uit twee delen. Het eerste deel stelt dat de integraal van een functie een primitieve functie is en het tweede doet de omgekeerde uitspraak: een primitieve functie geeft de integraal van een functie, op een constante na. Primitieve functie, primitieve, stamfunctie en onbepaalde integraal betekenen hetzelfde.
- Eerste deel
Zij een reële continue functie op het interval , dan is voor alle de functie , gedefinieerd door
differentieerbaar en een primitieve functie van , dat wil zeggen voor alle .
- Tweede deel
Het tweede deel van de stelling maakt duidelijk dat men de integraal van een functie kan berekenen aan de hand van een primitieve functie:
Zij een continue functie met primitieve functie , dan geldt:
Intuïtieve verklaring[bewerken | brontekst bewerken]
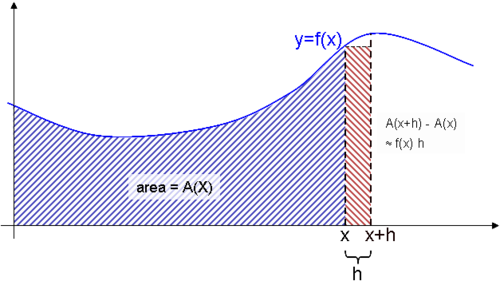
.
De bovenstaande uitspraken kunnen ook in een tekening aanschouwelijk gemaakt worden. De oppervlakte onder de grafiek van de functie , boven het interval is een functie van . Deze functie is dan de integraal van . Het verschil is de oppervlakte onder de grafiek boven het interval . Voor kleine is die oppervlakte ongeveer gelijk aan . Bijgevolg is:
In de limiet voor staat rechts de afgeleide van . In woorden: de afgeleide van de integraal is dus de oorspronkelijke functie .
Opmerking[bewerken | brontekst bewerken]
Merk wel op dat de primitieve functie van de afgeleide van een functie op een constante na kan verschillen van de oorspronkelijke functie. De primitieve functie is niet uniek: als een primitieve functie is van , is voor elke constante dat ook. Deze onbepaaldheid levert echter geen probleem op, indien men het verschil neemt van twee waarden van een primitieve functie, zoals de uitdrukking in hierboven.
Bewijs[bewerken | brontekst bewerken]
Om het eerste deel te bewijzen, moet men aantonen dat de afgeleide van . gegeven door
- ,
bestaat en gelijk is aan .
- Eerste deel
Kies een vaste en een voldoende kleine , zodat . Dan geldt
Vanwege de middelwaardestelling bestaat er een reëel getal tussen en , zodat voor het rechterlid geldt:
In de limiet voor , moet en dus ook vanwege de continuïteit van Bijgevolg is
Dit betekent precies dat de afgeleide van ter hoogte van bestaat en gelijk is aan .
- Tweede deel
Het bewijs van het tweede deel volgt uit het eerste. Stel dat men een primitieve functie heeft. Uit het eerste deel volgt dat ook de functie gedefinieerd als
een primitieve functie is. Bijgevolg zijn beide, als primitieve functies van , op een constante na gelijk: voor een bepaald getal . Dan is
Wat het tweede deel van de stelling bewijst.
Integreren[bewerken | brontekst bewerken]
Volgens de hoofdstelling is het berekenen van de oppervlakte onder een functie herleid tot het zoeken van een primitieve functie van . Stel dat men de oppervlakte onder de functie wil kennen, zeg tussen de punten en . De functie is een primitieve functie van .
Dankzij het verband met differentiëren kan men een aantal zeer nuttige rekenregels opstellen voor het uitvoeren van integralen. De productregel voor differentiëren kan men met de hoofdstelling vertalen naar de techniek van partiële integratie. Op analoge manier kan men de kettingregel gebruiken om de substitutieregel van integralen aan te tonen. Deze technieken maken het mogelijk van een zeer breed gamma aan functies de integraal te bepalen. Niet van elke functie is een primitieve functie te berekenen, maar van de meeste bekende functies wel.

![{\displaystyle f\colon [a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5ab61178bf5349838758ffe3d96135406ed0245)
![{\displaystyle [a,b]\subset \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a659536067aaaac2db1c44613a09a715f0cf7246)
![{\displaystyle x_{0}\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06636653315ee7c3b5dc9bdb6ac3fb8cccadc145)
![{\displaystyle F\colon [a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/22aae183016ffbb759663208b693d6a28be4e69e)



![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce)









![{\displaystyle [0,x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/725684c883c7ef386e8a0fe4d111e72c565747ed)
![{\displaystyle [x,x+h]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6273c65efb7394e51a3d13a2575cac8b4f184a1b)












![{\displaystyle x+h\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f4df501f24543eac232a9320622d9dd52d575e6)








![{\displaystyle F_{a}\colon [a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d18d551dc2f4c1b59c7de5eb299ab6e95ee18162)







