Liftkracht

Fig 1. Stroming om en krachten op een vleugel.

De liftkracht is de kracht die een stromend gas of vloeistof op een lichaam uitoefent loodrecht op de richting van de stroming.

Van liftkracht wordt gebruikgemaakt in de aerodynamica door de vleugels en roeren van een vliegtuig. Ook de propeller ontleent hier zijn voortstuwende kracht aan, net zoals zeilboten en windsurfplanken. Ook bij windturbines en windmolens is liftkracht het voortstuwende principe.

In de hydrodynamica wordt het principe gebruikt voor de voortstuwing door de schroef en besturing door het roer, maar ook bijvoorbeeld door draagvleugelboten.

Principes

De liftkracht is gedefinieerd als de kracht, loodrecht op de richting van de stroming (buiten het gebied waar de vleugel, het zeil of het wiekblad de stroming afbuigt). Voor vliegtuigen, die op constante hoogte vliegen is de liftkracht zuiver verticaal. In de andere gevallen (zeil, windturbineblad, molenwiek) moeten we rekenen met de schijnbare wind. Dit is de resultante van de windsnelheid en de snelheid van het zeil of blad zelf, en deze laatste snelheid kan vele malen groter zijn dan de windsnelheid.

Liftkracht is het gevolg van verscheidene effecten, zoals de reactiekracht van de lucht- of vloeistofstroom op het oppervlak, het Bernoulli-effect en het Coandă-effect.

Het effect van de reactiekracht is eenvoudig te begrijpen. Een vlakke plaat die een hoek maakt met de luchtstroom, zo dat de luchtstroom aan de onderzijde van de plaat wordt afgebogen, ondervindt behalve een reactiekracht in de richting van de stroom, ook een naar boven gerichte component. Deze reactiekracht is de belangrijkste component van de liftkracht bij vliegtuigvleugels.

Een platte plaat volstaat om vliegtuigen in de lucht te houden. Een vlakke vleugel is echter om meerdere redenen niet optimaal. Naast de vereiste neerwaartse kracht veroorzaakt een vlakke plaat ook turbulentie en luchtweerstand. Uit vele experimenten en berekeningen is gebleken dat de bovenkant van de vleugel beter een bolle vorm kan hebben. De luchtstroom volgt het vleugeloppervlak en buigt hierdoor ook aan de bovenkant van de vleugel naar beneden. Zonder deze bolle vorm zou de luchtstroom boven de vleugel bij een kleinere aanstromingshoek al loslaten (gewoon rechtdoor gaan) en zouden er luchtwervelingen ontstaan. Deze turbulentie werkt remmend en omdat de lucht aan de bovenkant van de vleugel niet meer afgebogen wordt, is er ook minder liftkracht. Deze bijdrage aan de totale liftkracht, die dus veroorzaakt wordt door het afbuigen van de luchtstroom, is gebaseerd op de Derde wet van Newton en wordt daarom wel de Newton-benadering genoemd.

De luchtsnelheidsverschillen boven en onder een vleugelprofiel kunnen met behulp van de Wet van Bernoulli worden omgerekend in drukverschillen, die ook weer liftkracht veroorzaken. De verklaring dat de lucht langs de bovenkant van de vleugel een langere weg moet afleggen en daarom sneller gaat stromen dan de lucht die onder de vleugel door gaat, is onjuist. We zouden dan immers ook wel een vleugel met een holle bovenkant of met heel veel hobbeltjes erin kunnen maken.

In professionele kringen rekent men met circulatie volgens de werveltheorie. Deze berekeningen zijn correct, maar geven weinig intuïtief inzicht in de aard van het ontstaan van liftkracht.

De verplaatsing van de vleugel door de lucht veroorzaakt aan de onderkant van een vleugel een overdruk en aan de bovenkant van de vleugel een onderdruk. Deze drukverschillen veroorzaken zelf nog een extra effect. De lucht aan de onderkant van de vleugel wordt door de overdruk ter plaatse afgeremd. Door de onderdruk boven de vleugel wordt de lucht naar de bovenkant van de vleugel gezogen. Dit veroorzaakt een grotere snelheid van de lucht boven de vleugel dan er onder. Daardoor wordt typisch 2/3 van de liftkracht aan de bovenkant van de vleugel geleverd en 1/3 aan de onderkant. De afbuigkrachten voor de luchtmassa zijn evenredig met het kwadraat van de luchtsnelheid.

Animatie van werking van liftkracht.

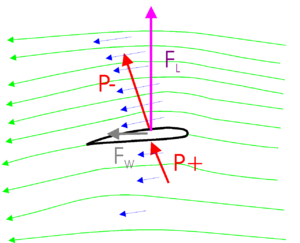
In nevenstaande figuur zijn om een dwarsdoorsnede van een vleugelprofiel stroomlijnen getekend (groen). Dit is het pad dat luchtdeeltjes afleggen als zij langs de vleugel stromen. In de lucht ver vóór de vleugel zijn ze op gelijke afstand getekend (bijvoorbeeld elke 5 meter). Als stroomlijnen dichter bij elkaar gaan lopen en de dichtheid blijft (ongeveer) gelijk, betekent dit dat de deeltjes sneller gaan stromen. De luchtsnelheid en stromingsrichting zijn aangegeven met de blauwe pijlen. De rode pijlen geven een indicatie van de onderdruk boven de vleugel en de overdruk er onder. Tenslotte geeft de paarse pijl de totale liftkracht weer en de grijze de weerstand. Men probeert de stromingsweerstand altijd zo laag mogelijk te houden. Bij een vliegtuig dat met constante snelheid op constante hoogte vliegt, is de liftkracht gelijk aan de zwaartekracht veroorzaakt door de massa van het hele vliegtuig en de voortstuwende kracht gelijk aan de weerstand van het vliegtuig.

Liftformule

Fig 2. Liftcoëfficiënt als functie van de aanstroomhoek.

De liftkracht L wordt als volgt berekend:

$L =\frac1 2\rho\cdot v^2\cdot S\cdot C_L(\alpha)$           (1)

waarin:

• $\rho$ is de dichtheid van lucht (in kg/m³ ; 1,23 kg/m³ op zeeniveau, 0,35 kg/m³ op 10 km hoogte);
• v is de luchtsnelheid (in m/s) ten opzichte van het opgelifte deel;
• S is het oppervlak (in m²) van het opgelifte deel;
• $C_L$ is de liftcoëfficiënt (dimensieloos) t.o.v $\alpha$ (aanstroomhoek).

In figuur 2 is de liftcoëfficiënt als functie van de aanstroomhoek gegeven. De aanstroomhoek (angle of attack) is de hoek die onbeïnvloede stroming maakt met de koorde van de vleugel (lijn van voorkant naar achterkant vleugel). C_L heeft voor veel profielen, zoals dat van figuur 1, al een positieve waarde bij aanstroomhoek 0°. Dat komt doordat de stroming over de gebogen achterkant al naar onder wordt afgebogen als de koorde van de vleugel evenwijdig met de stroming staat. Bij een bepaalde kritische hoek (10 à 20°) neemt de liftkracht plotseling zeer sterk af. Vliegtuigen mogen deze toestand van overtrek normaal gesproken niet bereiken. De curve is specifiek voor een bepaald profiel, maar heeft voor goede ontwerpen wel altijd ongeveer deze vorm.

Vliegtuigvleugels (en sommige scheepsroeren) hebben aan de achter- en/of voorkant 'flappen' of 'kleppen' (Engels: flaps en slats). Hiermee kan de lucht sterker naar onder of naar boven worden afgebogen. Daardoor wordt C_L en dus ook de liftkracht L groter (als de lucht meer naar beneden wordt afgebogen). Deze welvingskleppen worden gebruikt bij het opstijgen en landen.

Voor de liefhebber

Er wordt getwijfeld aan de feitelijke juistheid van het volgende gedeelte Raadpleeg de bijbehorende overlegpagina voor meer informatie, en pas na controle desgewenst het artikel aan.

Fig 3 Kracht op massa m

Een massa m die over een hoek α wordt afgebogen veroorzaakt (ondervindt) gedurende zekere tijd Δt een kracht F (centripetale kracht). Als we aannemen dat het afbuigpad cirkelvormig is met straal r, geldt:

$F = \frac {mv^2}{r}$     (2),

Waarin:

• F de kracht op de massa is in N
• v de snelheid van de massa in m/s
• r de straal in meters

De tijd dat de kracht F wordt uitgeoefend volgt uit:

$\Delta t = \frac{r\alpha}{v}$     (3),

zodat ((2) en (3) vermenigvuldigen):

$F\Delta t = \alpha m v\,$     (4).

Dus:

$F = \frac{\alpha m v}{\Delta t}$      (5)

De massa die in een tijd dt in een laagje lucht met hoogte h en breedte s stroomt:

$\frac{m}{dt} = \rho v s h$     (6)

Invullen van (6) in (5):

$F = \rho v^2 \alpha s h \,$     (7)

We kunnen (7) ook direct als volgt vinden:

We realiseren ons dat de lengte van de cirkelboog waarin de lucht wordt afgebogen gelijk is aan: $r.\alpha$. De massa m van een luchtstroom met hoogte h en breedte s, die op enig moment wordt afgebogen is dan:

$m = \rho h s r \alpha \,$.     (7a)

Invullen van (7a) in (2) levert direct (7) op.

Als we de snelheidsverdeling en de afbuighoek als functie van de hoogte zouden kennen kunnen we dit over de hoogte integreren. Deze verdeling is echter alleen met zeer ingewikkelde simulatieprogramma's te berekenen. We kunnen echter wel een zeer grove schatting maken van de hoeveelheid lucht die bij het proces is betrokken. Omdat bijvoorbeeld bekend is dat C_L = 1 is voor $\alpha$ = 10 º (0,17 radialen) kunnen we bij aanname van constante afbuighoek en constante luchtsnelheid, de verhouding van de totale hoogte h van de lucht uitrekenen die bij de afbuiging is betrokken.

We vervangen in de liftformule (1) A door s.b. dus we krijgen:

$F_L = C_L \rho \frac {v^2}{2} s b$      (8)

Door F_L uit (8) gelijk te stellen met F uit (7) en de eerder genoemde aanname voor afbuighoek (deze is groter dan de aanstroomhoek) en C_L te maken vinden we

$h = \frac{C_Lb}{2\alpha} = 3b$     (9)

De hoogte van de bij de afbuiging betrokken lucht blijkt dus 3 maal de vleugelbreedte te zijn, bij de gemaakte veronderstellingen. Er zij nogmaals benadrukt dat dit een zeer grove berekening is waarin heel veel zaken verwaarloosd of sterk vereenvoudigd zijn.

Er moet opgemerkt worden dat in werkelijkheid de lucht voor een groot deel eerst naar boven wordt afgebogen en pas daarna weer naar beneden. Het gaat bij de uiteindelijke kracht om de hoek die de wegstromende lucht maakt met de oorspronkelijke luchtstroom. Het feit dat de lucht boven de vleugel aanzienlijk sneller stroomt dan eronder maakt dat de onderdruk (dus druk ten opzichte van de lucht op grote afstand) boven de vleugel veel groter is dan de overdruk eronder (hier is de luchtsnelheid juist lager).

Nog een berekening

Een Boeing747 vliegt op 10 km hoogte met een snelheid van 900 km/uur met volle belasting (dit is een zeer extreem geval).

• Massa is 340.000 kg, dus zwaartekracht 3.332.000 Newton, de liftkracht F_L moet dus 3.332.000 Newton zijn.
• Vleugeloppervlak is 511 m².
• snelheid = 250 m/s
• dichtheid $\rho$ van de lucht op 10 km hoogte is 0,35 kg/m³.

We schrijven liftformule (1) in andere vorm:

$C_L = \frac {2F_L}{\rho v^2 A}$     (10)

We vinden dan na invulling van bovenstaande gegevens: C_L = 0,6

Dit lijkt gezien de bovenstaande plaatjes een redelijke waarde. Als het vliegtuig wat minder zwaar belast is (bijvoorbeeld totaal massa 2/3 van bovenstaande waarde), wordt C_L = 0,4. Het vliegtuig zal zo geconstrueerd worden dat het bij gemiddelde belasting horizontaal vliegt met de vleugelkleppen in een neutrale stand.

Het is ook aardig het drukverschil uit te rekenen. Dus zwaartekracht = liftkracht delen door vleugeloppervlak. We vinden dan voor het drukverschil bij maximale belasting: 6520 N/m². Gaan we uit van de 2/3 - 1/3 verhouding voor druk boven en onder de vleugel, dan vinden we overdruk onder de vleugel: 2170 N/m² en onderdruk boven de vleugel: 4350 N/m². De absolute luchtdruk op 10 km hoogte is 25.000 N/m². De drukverschillen zijn dus niet zeer klein ten op zichten van de luchtdruk: 17 % onderdruk boven de vleugel en 8 % overdruk onder de vleugel.

Aanbevolen literatuur

• "Introduction to Flight" van John D. Anderson, Jr, handboek dat gebruikt wordt aan de TU Delft bij Lucht- en Ruimtevaarttechniek.

Externe links

• (en) Animatie luchtstroom om vleugelprofiel
• (en) Zeer uitgebreide beschrijving over liftkrachten
• (en) Bernouilli versus Newton in de verklaring van liftkracht
• (en) Jef Raskins visie (Jef Raskin was een van de grondleggers van Apples Macintosh)
• (en) Een uitgebreide verhandeling van Boeing over flappen en liftkracht