Waterstofspectrum
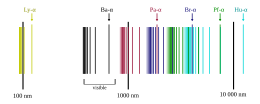
Het waterstofspectrum is de verzameling van golflengten (kleuren) van licht dat een waterstofatoom kan uitzenden. De bijbehorende frequenties worden gegeven door de formule van Johannes Rydberg. De spectraallijnen van waterstof zijn in de sterrenkunde van belang om waterstof aan te tonen en de snelheid van materie te bepalen met behulp van de roodverschuiving.
Energieniveaus[bewerken | brontekst bewerken]

Waterstof is het eerste element in het periodiek systeem. Het atoom bevat één proton en één elektron. Dit elektron kan zich slechts op wel bepaalde energieniveaus bevinden (zie atoommodel van Bohr). Wanneer het elektron zich van een hoger naar een lager energieniveau begeeft zendt het een foton uit waarvan de energie gelijk is aan het verschil van de twee energieniveaus. Bijgevolg kan het atoom slechts licht uitzenden van karakteristieke discrete frequenties: het zogenaamde spectrum. Dit spectrum is specifiek voor elk atoom en is een soort vingerafdruk van elk element. Zo kan men over grote afstanden de samenstelling van de sterren vaststellen door hun spectrum in spectraallijnen te ontleden door middel van astronomische spectroscopie.
Onderzoekers vonden wetmatigheden in de frequenties, die, zo bleek later, terug te voeren waren tot het energieniveau waarnaar de elektronen terugvielen. Zo zijn er de volgende reeksen:
| Naam van de reeks | Afkorting | Energieniveau | Golflengtes |
|---|---|---|---|
| Lyman | Ly | 1e | 121,6 - 91,1 nm |
| Balmer | Ba | 2e | 656 - 365 nm |
| Paschen | Pa | 3e | 1870 - 820 nm |
| Brackett | Br | 4e | 4050 - 1460 nm |
| Pfund | Pf | 5e | 7460 - 2280 nm |
| Humphreys | Hu | 6e | 12377 - 3280 nm |
De golflengte 656 nm die bij terugval van niveau 3 naar 2 ontstaat is de zogenaamde Hα-lijn, die de karakteristieke rode kleur van emissienevels veroorzaakt. In de Balmerreeks is het de overgang met het kleinste energieverschil tussen de elektronenbanen (orbitalen), dus de grootste golflengte. Naarmate het elektron uit een hogere baan terugkeert, wordt het energieverschil groter, de golflengte dus kleiner. Omdat de hogere orbitalen in energie steeds dichter op elkaar liggen, komen de spectraallijnen ook steeds dichter op elkaar te liggen.
Rydbergformule[bewerken | brontekst bewerken]
De energieverschillen tussen de niveaus in het Bohrmodel en daarmee ook de golflengten van de geabsorbeerde en uitgezonden fotonen worden gegeven door de Rydbergformule:[1]
met n het beginenergieniveau, n′ het uiteindelijke energieniveau en R de Rydbergconstante.[2] De formule levert alleen zinnige resultaten groter dan nul als n groter is dan n′. De limiet van is 0.
Reeksen[bewerken | brontekst bewerken]
Alle golflengten λ worden in nanometer met drie significante cijfers gegeven.
| Lymanreeks n′ = 1 |
Balmerreeks n′ = 2 |
Paschenreeks n′ = 3 |
Brackettreeks n′ = 4 |
Pfundreeks n′ = 5 |
Humphreysreeks n′ = 6 | ||
|---|---|---|---|---|---|---|---|
| 2 | 122 | Naam | |||||
| 3 | 103 | 656 | H - α | ||||
| 4 | 97,2 | 486 | H - β | 1870 | |||
| 5 | 94,9 | 434 | H - γ | 1280 | 4050 | ||
| 6 | 93,7 | 410 | H - δ | 1090 | 2630 | 7460 | |
| 7 | 397 | H - ε | 1000 | 2170 | 4650 | 12400 | |
| 8 | 954 | 1940 | 3740 | 7500 | |||
| 9 | 1820 | 3300 | 5910 | ||||
| 10 | 3040 | 5130 | |||||
| 11 | 4670 | ||||||
| ∞ | 91,1 | 365 | 820 | 1460 | 2280 | 3280 | |
De Lymanreeks is genoemd naar Theodore Lyman, die deze spectraallijnen ontdekte tussen 1906-1914. Alle golflengten in de Lymanreeks liggen in het ultraviolet.[3][4]
De Balmerreeks is genoemd naar Johann Jakob Balmer, die de empirische vergelijking formuleerde in 1885. Met de Balmerformule kunnen de golflengten van de spectraallijnen voorspeld worden. Balmerlijnen heten volgens de traditie "H-alfa", "H-beta", "H-gamma" enz., waarin H het element waterstof aanduidt.[5] Vier Balmerlijnen vallen in het zichtbare deel van het spectrum, met golflengten langer dan 400 nm. Delen van de Balmerreeks komen voor in het zonnespectrum. H-alfa is belangrijk in de sterrenkunde om waterstof aan te tonen.

De Paschenreeks is genoemd naar de Oostenrijks-Duitse natuurkundige Friedrich Paschen die haar het eerst waarnam in 1908. De Paschenlijnen liggen alle in het infrarood.[6]
De Amerikaanse natuurkundige Frederick Sumner Brackett nam de Brackettreeks als eerste waar in 1922.[7]
De Pfundreeks werd experimenteel ontdekt in 1924 door August Herman Pfund.[8]
De Humphreysreeks werd ontdekt door de Amerikaanse natuurkundige Curtis J. Humphreys.[9]
Rol in de astronomie[bewerken | brontekst bewerken]

De Balmerreeks wordt vaak gebruikt in de astronomie omdat waterstof het meest voorkomende element is in het heelal. Zo bijvoorbeeld om de ouderdom (spectraalklasse) van sterren vast te stellen. Jonge B- en A-sterren laten sterke Balmer-absorptielijnen zien in hun spectra.
Zie ook[bewerken | brontekst bewerken]
Bronnen, noten en/of referenties
|



