Driehoeksmeting
Een driehoeksmeting of triangulatie is een meetmethode die gebruikmaakt van het feit dat een driehoek volledig bepaald is als één zijde (de basis) en de aanliggende hoeken bekend zijn. De methode werd voor het eerst beschreven door de Nederlandse wiskundige Gemma Frisius (1508-1555). De cartograaf Jacob van Deventer (1505-1575) was de eerste die het in de praktijk omzette. Bij de driehoeksmeting wordt gebruikgemaakt van formules uit de goniometrie, met name de sinusregel.
In de landmeetkunde wordt de term driehoeksmeting vooral gebruikt voor het meten van een netwerk van vele driehoeken waarbij zo veel mogelijk hoeken gemeten worden en slechts één (of enkele) lengte van een driehoekszijde. De eerste die deze techniek beschreef en in praktijk bracht was Snellius (Willebrord Snel van Royen, 1580–1626). De methode werd in de 19e eeuw verfijnd door Carl Friedrich Gauss die een overbepaald stelsel van waarnemingsvergelijkingen met de kleinste-kwadratenmethode oploste.
Andere betekenis[bewerken | brontekst bewerken]
Triangulatie wordt als term ook gebruikt voor het verdelen van een veelvlak of een ander oppervlak in meerdere driehoeken. Dit principe wordt bijzonder veel gebruikt in de grafische industrie en geo-informatie om 3D modellen op een computer eenvoudig te kunnen verwerken voor computerspelletjes, animatiefilms en geografische informatiesystemen.
Basisprincipe[bewerken | brontekst bewerken]
De triangulatiemethode maakt gebruik van de wiskundige eigenschap van een driehoek dat haar vorm vastgesteld kan worden zonder dat al haar kenmerken bekend zijn. Een driehoek heeft 3 zijden (Z) en 3 hoeken (H), in totaal 6 kenmerken. Met drie van de zes kenmerken kan de driehoek al bepaald worden. Bijvoorbeeld: indien twee zijden ervan bekend zijn en de tussenliggende hoek (combinatie ZHZ), kan de rest uitgerekend worden. Er bestaan vijf combinaties waarvoor dit principe opgaat, alsmede één uitzondering: met de combinatie van 3 hoeken (HHH) is de schaal niet te bepalen.
Driehoeksmeting in een enkele driehoek: combinatie HZH[bewerken | brontekst bewerken]

Dit voorbeeld betreft een boot (B) die wordt waargenomen vanaf twee punten A en C op het strand. De onderlinge afstand b is bekend, of kan worden berekend uit de coördinaten van A en C, en zij vormt de basis van een driehoek met de boot als derde punt. De waarnemers in A en C meten elk de hoek die de zichtlijn naar de boot maakt met de basislijn. Met deze drie gegevens kan de positie van de boot in de driehoek worden berekend. De waarnemers kunnen nu ook de lengtes van de twee andere zijden uitrekenen en dus de afstand van elk punt tot de boot.
Dit wordt '(in)snijding' genoemd. Insnijding kan op twee manieren:
- Voorwaartse insnijding: Wanneer men beschikt over de positie (coördinaten) van twee bekende punten en men meet de richting van een nieuw punt vanuit die bekende posities, is de positie van het nieuwe punt uit te rekenen.
- Achterwaartse insnijding: Wanneer men beschikt over de coördinaten van ten minste drie punten, dan kan men met behulp van hoekmetingen vanuit het nieuw te bepalen punt naar de bekende punten, de positie bepalen, mits de drie punten en het te bepalen punt niet op één cirkel liggen.
Een netwerk van driehoeken: combinatie HZH[bewerken | brontekst bewerken]

In de landmeting wordt ook gebruikgemaakt van bovenstaande combinatie HZH, die in dit geval inhoudt:
- Als van één zijde de lengte bekend is en de twee aanliggende hoeken gemeten zijn, kan de lengte van de andere twee zijden berekend worden
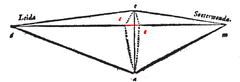
Daartoe wordt door landmeters één lengte handmatig en zeer nauwkeurig opgemeten, in de afbeelding hiernaast de lijn AB . Vervolgens wordt een afgelegen punt C gekozen, dat van beide uiteinden van deze lijn waargenomen kan worden. Met een theodoliet meet men dan de hoeken die de basislijn maakt met de zichtlijnen naar punt C. Daarna kunnen de lengten van die zichtlijnen (AC en BC) berekend worden. Omdat de lengten van die twee zichtlijnen daarmee bekend zijn, kunnen deze zelf weer als basislijn dienen voor een aan de eerste driehoek te koppelen tweede en derde driehoek (op de afbeelding naar de punten D, respectievelijk E). Door herhaling van deze methode kan op basis van slechts één daadwerkelijk gemeten lijn een keten of netwerk van driehoeken over grote afstanden berekend worden.
Ter controle van de uitkomsten kunnen op gezette plaatsen in deze keten berekende lijnstukken handmatig nagemeten worden. In het geval dat er extra lange zichtlijnen zijn, is het mogelijk controledriehoeken uit te zetten, die meerdere berekende driehoeken doorkruisen (de blauwe lijnen op de afbeelding).
Corrigeren voor hoogte[bewerken | brontekst bewerken]
Bovenstaande metingen werken perfect - in een plat vlak. Zelfs in een relatief plat land als Nederland worden soms meetpunten dicht bij de bodem gekoppeld aan kerktorens, zodat voor hoogteverschillen gecompenseerd moet worden om afstanden in een rechte lijn te kunnen berekenen. De hoogte van waargenomen punten kan eveneens met driehoeksmeting worden vastgesteld, met behulp van de combinatie van kenmerken: één bekende zijde, een aanliggende hoek en de tegenoverliggende hoek (HHZ).
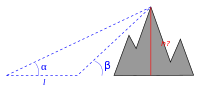
In nevenstaande afbeelding wordt eerst een driehoek opgemeten (blauw), met de lijn als basis, via de hoeken en (HZH). Van de rechter stippellijn is nu de lengte bekend en de denkbeeldige voortzetting van de basislijn maakt een rechte hoek (90°) met de verticale lijn , de gevraagde hoogte , die eenvoudig berekend kan worden als:
Hierbij moet worden aangetekend dat op de afbeelding de gemeten basislijn geacht wordt zich horizontaal (waterpas) en op zeeniveau te bevinden. De omstandigheden in het veld zijn doorgaans niet zo ideaal, hetgeen steeds complexere berekeningen vereist.
Rijksdriehoeksmeting[bewerken | brontekst bewerken]

Met behulp van driehoeksmeting zijn de coördinaten van de originele punten van het Nederlandse stelsel van rijksdriehoeksmeting (RD) bepaald. Op deze wijze zijn veel landen voor het eerst opgemeten. Vanwege hun zichtbaarheid werden in Nederland vooral kerktorens gebruikt als referentiepunten bij de driehoeksmetingen in plaats van heuveltoppen. Deze punten vervullen de rol van hoekpunt in een of meerdere driehoeken. De eerste landsdekkende driehoeksmeting in Nederland maakte gebruik van een basis in Duitsland in de buurt van Bonn, de meting Vrouwenheide (Ubachsberg) - Klifsberg (gemeente Herkenbosch) vormde de aansluiting met de rest van Nederland. In 1913 is in Stroe een basis gemeten ter controle van het doorgerekende driehoeksnet en de gemeten afwijking bleek verwaarloosbaar.
Zie ook[bewerken | brontekst bewerken]
Bronnen, noten en/of referenties
|







