Halfregelmatig veelvlak

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
|

|

|

|

Een halfregelmatig veelvlak is een convex driedimensionaal object dat uit regelmatige veelhoeken is opgebouwd.
Een veelvlak heet halfregelmatig als:
- alle zijvlakken een regelmatige veelhoek zijn en
- het veelvlak hoekpunttransitief is, maar
- geen regelmatig veelvlak is.
De halfregelmatige veelvlakken vallen uiteen in drie categorieën:
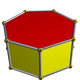
- een oneindige serie prisma's - hoekpuntconfiguratie .4.4, = 3, 5, 6, 7, ..
- een oneindige serie antiprisma's - hoekpuntconfiguratie .3.3.3, = 4, 5, 6, 7, ..
- 13 archimedische lichamen, 15 als ook de spiegelbeelden van de stompe dodecaëder en de stompe kubus worden meegerekend
De hoekpuntconfiguratie is binnen de regelmatige en halfregelmatige veelvlakken uniek, behalve dat van de archimedische lichamen 3.3.3.3.4 en 3.3.3.3.5 elk twee chirale vormen bestaan, die elkaars spiegelbeeld zijn.
Een nodige voorwaarde ervoor dat het veelvlak hoekpuntransitief is, is dat in ieder hoekpunt steeds dezelfde veelhoeken in dezelfde of tegengestelde volgorde samenkomen. De gedraaide romboëdrisch kuboctaëder illustreert dat dit geen voldoende voorwaarde is: in ieder hoekpunt komen steeds dezelfde veelhoeken in dezelfde of tegengestelde volgorde samen, drie vierkanten en een driehoek, maar toch is er geen isometrie die het veelvlak op zichzelf afbeeldt.[1] Het is een johnsonlichaam.
De johnsonlichamen zijn uit ook alleen regelmatige veelhoeken opgebouwd, maar niet hoekpunttransitief. Dat zijn dus geen halfregelmatige veelvlakken.
Bronnen, noten en/of referenties
|

