Kaartschaal

De kaartschaal, kortweg vaak schaal, is de verhouding tussen een afstand op de kaart en de overeenkomstige afstand in werkelijkheid. De schaal kan worden weergegeven in een verhouding zoals 1 : 25.000. De schaal 1 : 25.000 is een grotere schaal dan 1 : 50.000, omdat 1 / 25.000 groter is dan 1 / 50.000. Op een kaart met grote schaal kunnen dan ook per oppervlakte-eenheid in de werkelijkheid meer gegevens en meer details getoond worden dan op een kaart met een kleinere schaal zonder dat de leesbaarheid nadelig beïnvloed wordt.
Bij een fysieke kaart (meestal van papier) geldt daadwerkelijk zo'n verhouding. Bij een digitale kaart die bekeken wordt op een beeldscherm is zo'n schaal in de letterlijke zin afhankelijk van in- en uitzoomen en van de grootte van het beeldscherm en/of het venster op het beeldscherm, en dus niet een eigenschap van de data. Een schaalaanduiding van een digitale kaart als eigenschap van de data is een indicatie van de gedetailleerdheid van de informatie, en de positionele nauwkeurigheid. Bij inzoomen van een rasterkaart wordt de kaart wazig of blokkerig, en worden lijnen dikker en teksten groter. Bij inzoomen van een vectorkaart met nauwkeurige data worden deze nauwkeuriger grafisch weergegeven, en worden lijnen niet noodzakelijk dikker. Kaartsoftware met een aparte laag voor tekst kan eventueel teksten bij inzoomen niet meevergroten (wat overigens lastig is als men juist zou willen inzoomen om een tekst, symbool of kaartdetail beter te kunnen lezen/bekijken).
Vaak is kaartsoftware zodanig dat bij inzoomen meer details (bijvoorbeeld extra objecten) worden weergegeven, en wordt dus niet slechts een digitale kaart groter weergegeven, maar wordt een meer gedetailleerde digitale kaart getoond (en omgekeerd bij uitzoomen). Zie ook Beeldschermcartografie.
Een op de kaart getekende schaalstok is een schaalaanduiding die onafhankelijk van in- en uitzoomen enz. te interpreteren is.
Geschiedenis[bewerken | brontekst bewerken]
Voordat de metrieke schaal rond het midden van de 19e eeuw zijn opgang deed werd er voordien voornamelijk gebruik gemaakt van grafische schalen, bijv. door een schaalstok. Deze was minder nauwkeurig en vaak gebaseerd op lokale meeteenheden, bijv. roeden, voeten, mijlen of 'uren gaans'.
Voorbeelden van schalen[bewerken | brontekst bewerken]
Enkele voorbeelden van schalen:
- 1 : 25 000: 4 centimeter op de kaart is 1 kilometer in werkelijkheid
- 1 : 100 000: 1 centimeter op de kaart is 1 kilometer in werkelijkheid
- 1 : 1 000 000: 1 centimeter op de kaart is 10 kilometer in werkelijkheid
In Angelsaksische landen zijn andere schalen gebruikelijk, bijvoorbeeld:
- 1 : 63 360: 1 inch op de kaart is 1 mijl in werkelijkheid ('inch map')
- 1 : 253 440: 1 inch op de kaart is 4 mijl in werkelijkheid ('quarter inch map')
Kaartprojectie[bewerken | brontekst bewerken]
Het verloop van de schaal is afhankelijk van de kaartprojectie. Een bol of ellipsoïde kan niet zonder vervormingen worden overgezet naar een plat vlak (zo'n oppervlak is niet ontwikkelbaar). Daardoor is over het algemeen de schaal in een punt van de kaart in verschillende richtingen niet gelijk en bovendien verschillend van punt tot punt. Dit wordt de voorstellingsschaal genoemd. De schaal van de kaart in zijn geheel wordt de nominale of principale schaal genoemd. Deze schaal geldt in een centraal punt van de kaart. De verhouding tussen de voorstellingsschaal en de nominale schaal wordt de schaalfactor genoemd.
Als de schaal van de kaart langs een bepaalde lijn, in de richting van die lijn constant is, dan spreekt men van equidistantie of afstandsgetrouwheid langs die lijn. Een platte kaart die vanaf elk willekeurig punt in alle richtingen afstandsgetrouw is kan niet worden gemaakt, dit kan slechts langs bepaalde lijnen. Deze lijnen kunnen ontspringen aan één punt (radiaal) of parallel langs elkaar liggen. Langs lijnen die uit een ander punt ontspringen respectievelijk die niet parallel lopen, geldt die afstandsgetrouwheid niet.
Voorbeelden van afstandsgetrouwe projecties zijn:
- equidistante azimutale projectie, radiaal
- equidistante cilinderprojectie, langs meridianen
- sinusoïde projectie, langs parallellen
- tweepunts-equidistante projectie, vanaf twee punten
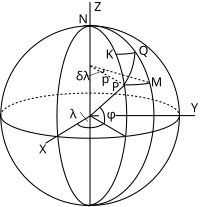
De voorstellingsschaal in punt P op breedte en lengte in de richting naar Q kan worden geschreven als:
Vervormingen[bewerken | brontekst bewerken]

De vervormingen die optreden door de projectiemethode om een bolvormig oppervlak om te zetten naar een plat vlak zijn weer te geven met behulp van de indicatrix van Tissot. Als de schalen in de hoofdrichtingen gelijk zijn, dan zijn de halve lange as en de halve korte as van deze ellips gelijk en daarmee cirkelvormig. In deze conforme of hoekgetrouwe projectie is de schaal dus niet afhankelijk van de richting. Dit is het geval bij de mercatorprojectie. De schaal is daar wel afhankelijk van de breedtegraad.
Weergave wegen op wegenkaarten[bewerken | brontekst bewerken]
Op een wegenkaart zijn de wegen bijna altijd te breed afgebeeld. Zou men dat niet doen, dan worden de wegen onzichtbaar dunne lijntjes. Het gevolg daarvan is dat knooppunten niet altijd goed kunnen worden weergegeven: wat er op de kaart uitziet als een kruising, kan in werkelijkheid twee T-splitsingen zijn. Is een weg met twee rijbanen (of een fietspad) getoond, dan is de afstand tussen de rijbanen in werkelijkheid minder dan de kaart aangeeft.
Tweede, impliciete betekenis van (kaart)'schaal'[bewerken | brontekst bewerken]
Een schaal op een kaart zegt - behalve direct over de verhouding - zoals gezegd ook iets over de nauwkeurigheid. Een schaal, bedoeld voor en ingewonnen op een kleinschalig niveau, toont minder objecten en minder nauwkeurig geplaatste objecten dan een grootschalige kaart. Doordat kaarten vrijwel allemaal gedigitaliseerd zijn, en beschikbaar via GIS-systemen, is het mogelijk zeer ver op kaarten in te zoomen; het schaalniveau zegt daardoor eerder iets over de nauwkeurigheid. Ook als een kaart wellicht alleen ingewonnen is om te dienen voor een bepaalde schaal, kunnen gebruikers op 'onnauwkeurig' ingetekende objecten flink inzoomen. Bij grootschalig gebruik kan dat tot problemen leiden, wanneer men dit niet beseft. Gebruikers dienen dus, bij het meten in kaart(beelden), bij het printen op wat voor schaal dan ook, en bij het combineren van verschillende kaarten, rekening te houden met de oorspronkelijke schaal. Kleinschalige kaarten zouden op bepaalde grootschalige kaartniveaus feitelijk niet meer in beeld mogen komen. De schaal geeft in een GIS impliciet (voor een cartograaf of GIS-specialist: expliciet) de nauwkeurigheid van de objecten. De oorspronkelijke schaal of de inwinningsschaal geeft aan de gebruiker of ontwerper van een GIS de informatie over hoe de kaart gebruikt mag worden. Bijvoorbeeld: een wegenkaart van Europa (schaal 1 : 5 000 000), gecombineerd met een andere, nauwkeurige gps-locaties van benzinestations in Nederland (schaal 1 : 10 000) levert vreemde effecten op in de plot, ingezoomd op een van die benzinestations; de benzinestations lijken dan aan de verkeerde kant van de weg te liggen, terwijl feitelijk gezien de weg niet verkeerd is ingetekend; op de oorspronkelijk bedoelde schaal was de nauwkeurigheid groot genoeg, en lag 'op de juiste plek'; te ver ingezoomd ligt deze weg blijkbaar toch verkeerd.
Literatuur[bewerken | brontekst bewerken]
- Draaisma, Y; Meester, J.J.; Mulders, J.H.; Spaans, J.A. (1986): Leerboek navigatie, deel 2, De Boer Maritiem;
- Schaal (1991). In Kartografisch woordenboek, Nederlandse Vereniging voor Kartografie;
- Maeyer, Ph. De; Vliegher, B.M.; Brondeel, M. (2004): De spiegel van de wereld: fundamenten van de cartografie, Academia Press.
- Smits, Jan (2015): Mathematical data for bibliographic descriptions of cartographic materials and spatial data, ICA Commission on Maps Projection.




