Mercatorprojectie

Mercatorprojectie
Gunstige eigenschap	hoekgetrouw en lijnen van constante kompaskoers zijn recht
Niet-geometrische bewerkingen	breedte-afhankelijke schaling
Geometrische constructie
Vorm van het projectievlak	cilinder
Positie van het projectievlak	normaal
Rakend/snijdend	rakend
Portaal    Geografie

Een kaart van Blaeu volgens de mercatorprojectie.

De normale conforme projectie of mercatorprojectie, ook wel wassende kaart of vergrotende breedtekaart, is een kaartprojectie die genoemd is naar de Vlaamse cartograaf Gerardus Mercator, die deze projectie in 1569 introduceerde. De projectie is hoekgetrouw of conform. Dit wil zeggen dat de hoeken tussen verschillende richtingen op de kaart gelijk zijn aan de hoeken tussen die richtingen op het aardoppervlak. Dit betekent onder andere dat alle meridianen er verticaal, en alle parallellen onderling loodrecht staan.

Loxodroom

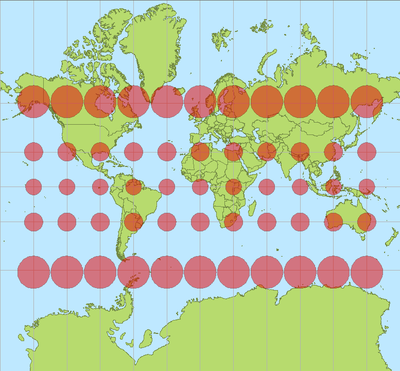
De mercatorprojectie is van groot belang voor de scheepvaart, omdat een lijn van constante kompaskoers (loxodroom) op de kaart een rechte lijn is. Hoewel de projectie daarom, zeker in het verleden, veelvuldig is toegepast en in de scheepvaart nog steeds, wordt zij tegenwoordig voor meer algemene wereldkaarten in atlassen en dergelijke minder geschikt geacht. Geen enkele projectie kan de Aarde weergeven op een plat vlak zonder vervormingen weer te geven. Bij de mercatorprojectie treden oppervlaktevervormingen op, waarbij gebieden groter worden weergegeven naarmate ze verder van de evenaar liggen; op de polen zelf treedt zelfs een oneindige vergroting op. Volgens deze projectie is Groenland ongeveer even groot als het continent Afrika, terwijl het in werkelijkheid zo'n 17 maal kleiner is, dat wil zeggen: zo groot als het Arabisch schiereiland. Een ander nadeel is dat de kortste route tussen twee punten, de orthodroom, geen rechte lijn is bij deze kaartprojectie.

Op hogere breedte wordt de projectie van de breedtegraden steeds groter, de zogenaamde vergrotende breedte. Om hoekgetrouwheid of conformiteit te bereiken, is de projectie echter niet rechtstreeks.

De mercatorprojectie is een cilinderprojectie, dat wil zeggen dat de afbeelding tot stand komt door de bol te projecteren op een cilinder die de bol precies omsluit. Het is echter geen rechtstreekse projectie. Om hoekgetrouwheid te bereiken, wordt een breedte-afhankelijke schaalcorrectie toegepast, de vergrotende breedte. Op de evenaar is de afstand van een lengtegraad vrijwel gelijk aan een breedtegraad, aangezien beiden grootcirkels zijn. Aangezien de parallellen kleincirkels zijn, wordt op hogere breedte de afstand van een lengtegraad echter steeds kleiner, om uiteindelijk op de polen nul te worden. Bij de mercatorprojectie houden de lengtegraden echter een gelijke lengte, zodat de breedtegraden vergroot moeten worden om de onderlinge verhouding tussen de afstand van een lengtegraad en een breedtegraad kloppend te houden. Hierdoor rekt de kaart richting de polen steeds meer op. Na 'uitrollen' van de cilinder ontstaat een vlakke kaart.

De projectie wordt beschreven door:

$x\ = r\,\lambda$

$y\ = r\,\ln\left[\tan\left(\frac{\pi}{4} + \frac{\varphi}{2}\right)\right]$

Waarbij λ de lengtegraad is en φ de breedtegraad.

De formules zijn afkomstig van Edward Wright, niet van Mercator zelf.

Een variatie op de mercatorprojectie is de Universele Transversale Mercatorprojectie (UTM), die in feite een combinatie is van een aantal projecties op steeds een aantal graden verdraaide 'horizontaal' geplaatste cilinders.

Schaal

Indicatrix van Tissot van de mercatorprojectie. Bij deze projectie is de schaal niet afhankelijk van de richting, wat tot uiting komt in de cirkelvorm van de ellipsen. De schaal is wel afhankelijk van de breedte, wat tot uiting komt in het groter worden van de cirkels op hogere breedte. In afwijking van de theorie van Tissot zijn de cirkels niet infinitesimaal klein vanwege de zichtbaarheid.

Bij mercatorkaarten wordt de breedtegraad gegeven waarvoor de schaal geldt, aangezien deze groter wordt met toenemende breedte; de vergrotende breedte. De schaal op de evenaar s₀ verhoudt zich tot de schaal op breedtegraad b s_b volgens de schaalformule:

$s_b = { s_0 \over \cos b}$

Vanwege deze veranderende schaal moeten 'verheden', zoals afstanden in het jargon heten, op een mercatorkaart worden afgepast op de middelbreedte — de gemiddelde breedtegraad van een traject — met staande randminuten, de meridiaanminuten die de zijrand van de kaart vormen.

Vanwege het toenemen of 'wassen' van de staande randminuten wordt een mercatorkaart ook wel wassende kaart genoemd.

Zie ook

• Transversale Mercatorprojectie