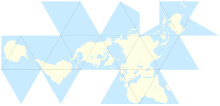
Kaartprojectie

Een kaartprojectie is een wiskundige afbeelding die het aardoppervlak, de sterrenhemel of het oppervlak van een ander hemellichaam of een deel daarvan op een vlakke kaart overbrengt. Als wordt afgezien van de afplatting van de Aarde, is dit een afbeelding van een boloppervlak of een deel daarvan op een plat vlak.
In een aantal gevallen correspondeert de afbeelding, afgezien van de schaling naar het formaat van een fysieke kaart op papier of een beeldscherm, met een meetkundige projectie op een ontwikkelbaar oppervlak, en het vervolgens plat leggen daarvan. Dit wordt als echte projectie aangeduid. Dit gaat voor de meeste kaartprojecties niet op, die worden als onechte projectie aangeduid. 'Projectie' wordt dan in een meer algemene zin gebruikt.
Het is niet mogelijk het aardoppervlak zonder vertekening weer te geven op een plat vlak, het aardoppervlak is zelf geen ontwikkelbaar oppervlak. Er zijn dan ook veel kaartprojecties met verschillende eigenschappen. Afhankelijk van de aan de kaart gestelde eisen en het af te beelden gebied, is een projectie meer of minder geschikt.
Met elke kaartprojectie, inclusief schaal, correspondeert na keuze van een oriëntatie en een oorsprong, een coördinatenstelsel voor de horizontale positie van punten op het betreffende deel van de Aarde, namelijk de cartesische coördinaten op de kaart. De vierkante platkaart correspondeert bijvoorbeeld met geografische coördinaten (lengtegraad en breedtegraad), waarbij de keuze van uniforme schaling kan worden uitgedrukt in de afstand die correspondeert met een breedtegraad. Deze laatste verschilt per computerscherm en mate van inzoomen (of hoe groot de kaart op papier is afgedrukt), en kan, afhankelijk van de context, worden gezien als iets dat los staat van de kaartprojectie. Formeel kan een kaartprojectie dan gezien worden als een equivalentieklasse van de betreffende afbeeldingen, waarbij equivalentie van twee afbeeldingen betekent dat de ene een uniforme verschaling is van de andere.
Nationale geodetische coördinatensystemen worden op de genoemde wijze gedefinieerd, uitgaande van een kaartprojectie die bij het betreffende land past. De projectie wordt vaak hoekgetrouw gekozen en, met coördinaten in meters, met een schaal die zo goed mogelijk 1:1 benadert. Hier wordt zo ook de keuze van uniforme schaling bij het bekijken van de kaart gescheiden gehouden van de kaartprojectie.
Meetkundige projecties[bewerken | brontekst bewerken]
Een meetkundige kaartprojectie kan men zich voorstellen als een doorzichtig model van een deel van het aardoppervlak (als een dia in de vorm van een deel van een bol), dat op een projectiescherm wordt geprojecteerd. De lichtbron bevindt zich op grote afstand (parallelprojectie) of bijvoorbeeld in het centrum of op het oppervlak van de bol (puntprojectie). Het projectiescherm kan een kegel zijn, of de uitersten daarvan: een cilinder of een plat vlak. Afhankelijk van de plek van de 'lichtbron', de oorsprong van de projectie, en de vorm en positie van het 'projectiescherm' (het kaartbeeld) ontstaan allerlei verschillende soorten projecties met uiteenlopende eigenschappen. Soms wordt een projectie in algemenere zin beschreven in termen van een meetkundige projectie, maar dan met de plek van de 'lichtbron' afhankelijk van het geprojecteerde punt op het aardoppervlak. Bij bijvoorbeeld de orthografische cilinderprojectie is de 'lichtbron' op de cilinderas, maar de positie daarop hangt af van de breedtegraad van het geprojecteerde punt. Fysiek kan men zich dit voorstellen als lampjes op de as die door afscherming alleen in de richtingen loodrecht op de as (rondom) schijnen.
Vorm van de Aarde[bewerken | brontekst bewerken]
De vorm van de Aarde heeft een grillig verloop dat ongeschikt is om te dienen als uitgangspunt bij het vervaardigen van een kaart. Om toch een kaart mogelijk te maken, wordt gebruikgemaakt van benaderingen. In toenemende mate van benadering van de werkelijke vorm zijn dit de bol, de omwentelingsellipsoïde en de geoïde. De projectie wordt soms gedefinieerd als een combinatie van twee stappen, de projectie van de geoïde op een rekenbol, en een kaartprojectie voor die bol.
Bol[bewerken | brontekst bewerken]
Indien de nauwkeurigheid niet zo groot hoeft te zijn, zoals bij wereldkaarten en andere kaarten op kleine schaal, kan de Aarde als bol worden beschouwd. Zoals gezegd zijn deze projecties ook van belang als tweede stap in een meer geavanceerde projectie.
Ellipsoïde[bewerken | brontekst bewerken]
Isaac Newton berekende reeds in de 17e eeuw op theoretische gronden dat de Aarde als gevolg van de zwaartekracht enerzijds en de middelpuntvliedende kracht anderzijds geen bol is, maar een oblate ellipsoïde met afgeplatte polen. Later werd die afplatting nauwkeurig berekend.
Er zijn verschillende referentie-ellipsoïdes in gebruik die verschillen in vorm, afmetingen, positie, oriëntatie en schaalfactor. Zo zijn oudere ellipsoïdes in gebruik die goed aansluiten bij de lokale geoïde, maar die wereldwijd niet goed bruikbaar zijn. Tegenwoordig zijn ellipsoïdes in gebruik met het massacentrum van de Aarde als oorsprong, zoals GRS80.
Geoïde[bewerken | brontekst bewerken]
De vorm van de Aarde wordt benaderd met de geoïde, het vlak op gemiddeld zeeniveau waar dezelfde zwaartekrachtspotentiaal heerst, een equipotentiaalvlak. De geoïde is onregelmatig van vorm, waardoor hier alleen lokaal een eenvoudig wiskundig model voor te maken is. Voor grotere gebieden wordt de geoïde gemodelleerd met polynomen of interpolatie van een regelmatig raster.
Vormen van projectie[bewerken | brontekst bewerken]
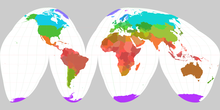
De indeling van meetkundige projecties naar projectieoppervlak (kegelprojectie, cilinderprojectie en projectie op een plat vlak) is in veel gevallen uitbreidbaar naar 'onechte' projecties, doordat die kunnen worden opgevat als verkregen door een meetkundige projectie, met vervolgens verdere bewerkingen om gewenste eigenschappen te krijgen. Nog verdergaande bewerkingen leveren bijvoorbeeld de pseudo-cilindrische oppervlaktegetrouwe sinusoïdeprojectie en de Robinsonprojectie op. Projecties die bij deze indeling vallen in de categorie "op een plat vlak" zijn meestal azimutale projecties.
De meetkundige projecties worden verder ingedeeld naar de plaats van de oorsprong ('lichtbron'). Het projectieoppervlak wordt in het algemeen ontwikkelbaar gekozen, het kan dan gemakkelijk zonder tweede projectie tot een plat vlak worden gemaakt. Na de keuze voor een projectieoppervlak, kan dit op verschillende manieren tegen (of gedeeltelijk 'in') de rekenbol worden geplaatst, meestal zodanig dat het af te beelden deel van de wereld in het midden van de kaart terechtkomt, waar de vervormingen het kleinst zijn.
| Kegelprojectie | Cilinderprojectie | Azimutale projectie | |
|---|---|---|---|
| Projectieoppervlak |  Het projectieoppervlak is een kegelmantel. |
 Het projectieoppervlak is een cilindermantel. |
 Het projectieoppervlak is een plat vlak. |
| Ligging |  De ligging kan normaal, transversaal of scheef zijn. Bij een normale ligging valt de centrale as samen met de aardas, terwijl deze bij een transversale ligging negentig graden gedraaid ligt ten opzichte van normaal. Een scheve, oblique, ligging valt tussen beide in. | ||
| Contact |   Het projectieoppervlak kan het aardoppervlak raken, maar ook snijden. De vervorming is minimaal waar het projectieoppervlak het aardoppervlak raakt. In sommige gevallen geldt dit ook waar het projectieoppervlak het aardoppervlak snijdt. Bij projectie vanuit een punt op een plat vlak is alleen de stand van het vlak van belang: evenwijdige vlakken, mits niet door het punt, geven behoudens de triviale uniforme verschaling hetzelfde resultaat. | ||
| Oorsprong De oorsprong van een meetkundige projectie, het 'lichtpunt', kan op verschillende plaatsen ten opzichte van de rekenbol gekozen worden |
    Bij de gnomonische of centrale projectie ligt de oorsprong van de projectie in het centrum van de rekenbol. Bij de stereografische projectie ligt de oorsprong diametraal tegenover het raakpunt op de andere kant van de rekenbol. Bij orthografische projectie wordt loodrecht op een oppervlak geprojecteerd (bij orthografische cilinderprojectie is daarbij de oorsprong afhankelijk van een van beide coördinaten van het geprojecteerde punt). Bij afbeelding op een plat vlak komt dat overeen met een oorsprong op grote afstand. Bij de perspectiefprojectie ligt de oorsprong buiten de aardbol en wordt het dichtstbijgelegen deel van de bol afgebeeld. | ||
| Hoekgetrouwe projecties Een hoekgetrouwe of conforme kaart laat hoeken intact en beeldt daardoor een kleine vorm op de rekenbol bij benadering gelijkvormig af op de kaart |
 Conforme kegelprojectie van Lambert |
 Normale conforme projectie |
 Stereografische projectie |
| Oppervlaktegetrouwe projecties De schaal van de equivalente kaart kan variëren, maar de verhouding van de oppervlakten van twee gebieden op de kaart is gelijk aan de verhouding van hun oppervlakten in werkelijkheid |
 Equivalente kegelprojectie |
 Cilinderprojectie van Lambert |
 Azimutale projectie van Lambert |
| Equidistante projectie Op een afstandsgetrouwe of equidistante kaart is de schaal langs bepaalde lijnen onafhankelijk van het punt op zo'n lijn. Deze lijnen kunnen ontspringen aan één punt (radiaal) of parallel langs elkaar liggen. Langs lijnen die uit een ander punt ontspringen respectievelijk die niet parallel lopen geldt die afstandsgetrouwheid niet |
 Equidistante kegelprojectie |
 Kwadratische platkaart |
 afstandsgetrouwe azimutale projectie |
Gewenste eigenschappen[bewerken | brontekst bewerken]
Door de keuze van bovenstaande parameters en als gevolg van eventuele nabewerkingen krijgt de kaart bepaalde eigenschappen. Gewenste eigenschappen kunnen zijn:
- hoekgetrouw, conform, stereografisch
- hoeken blijven intact, de kaart beeldt daardoor een kleine vorm op de bol bij benadering gelijkvormig af op de kaart;
- oppervlaktegetrouw, equivalentie
- de verhouding van de oppervlakten van twee gebieden op de kaart is gelijk aan de verhouding van hun oppervlakten in werkelijkheid;
- behoud van kortste weg, gnomonische projectie
- alle grootcirkels zijn op de kaart rechten, rechte lijnen op de kaart geven dus de kortste weg tussen twee punten aan;
Eigenschappen gerelateerd aan bepaalde punten of lijnen:
- grootcirkels door één bepaald punt vormen rechte lijnen, gecombineerd met hoekgetrouwheid in dit punt, en daarmee richtinggetrouwheid vanuit dit punt
- afstandsgetrouw of beperkt afstandsgetrouw
- op een afstandsgetrouwe of equidistante kaart is de schaal langs bepaalde lijnen onafhankelijk van het punt op zo'n lijn. Deze lijnen kunnen ontspringen aan één punt (radiaal), twee punten (tweepunts-equidistante projectie) of parallel langs elkaar liggen.
- de rechten op de kaart corresponderen met vaste kompasrichtingen. Deze eigenschap is daarmee gekoppeld aan de aardas, dus gerelateerd aan de keuze van een as door de bol, het zijn loxodromen;
Sommige projecties corresponderen niet met de hele bol, de gnomonische projectie bijvoorbeeld met hoogstens een halve. Er zijn ook projecties die in theorie een oneindig grote kaart opleveren, waarbij een eindige kaart dus niet de hele bol weergeeft en er zijn kaarten met een extra lange rand, met bijvoorbeeld inkepingen, die een oceaan in twee delen tonen. Als gewenste eigenschap kan dus gelden dat de kaart de hele bol bestrijkt en geen extra randen heeft.
Elk van de bovenstaande eigenschappen is in principe gunstig, maar ze gaan maar zeer beperkt samen. Hoekgetrouwheid en oppervlaktegetrouwheid gaan bijvoorbeeld nooit samen. Als geen van deze eigenschappen bereikt zijn spreekt men van een afylactische projectie. Het gaat dan vaak om een compromis tussen onverenigbare eigenschappen, zoals bij de Winkel-tripelprojectie.