Kegel (ruimtelijke figuur)

Een kegel of conus is een ruimtelijke figuur die bestaat uit een cirkelschijf, de basis, en een gekromd vlak, de mantel of zijde, gevormd door alle lijnstukken tussen de punten van de cirkel en een vast punt, verschillend van het middelpunt van de cirkel en loodrecht daarboven, de top van de kegel. Het verbindingslijnstuk van de top met het cirkelmiddelpunt is de as van de kegel.
Ook het lichaam dat bestaat uit de bovengenoemde vlakken samen met de punten in het inwendige wordt kegel genoemd.
Meer algemeen is in de meetkunde een kegel of conus een ruimtelijke figuur die ontstaat door alle punten van een begrensd en samenhangend deel van een plat vlak, de basis, te verbinden met een punt, de top, gelegen buiten dat vlak. Er is geen uniformiteit wat de definitie betreft. De basis kan bijvoorbeeld beperkt zijn tot gesloten vlakke krommen, of tot een daardoor omsloten gebied.
Kegelsneden[bewerken | brontekst bewerken]
In de meetkunde wordt met een kegel ook wel de onbegrensde ruimtelijke figuur bedoeld, die vanuit de bovenstaande figuur kan worden gemaakt door het bodemvlak weg te nemen, en die boven het bovenste puntje omgekeerd wordt herhaald. Van deze dubbele oneindige kegel zijn snijvlakken met een plat vlak bekend als de kegelsneden: cirkel, ellips, parabool en hyperbool. Strikt genomen zijn geïsoleerde punten en tweetallen elkaar snijdende rechten ook kegelsneden, maar deze worden ontaard genoemd om ze van deze vier te onderscheiden.
Oppervlakte en inhoud[bewerken | brontekst bewerken]
De oppervlakte van een kegel is: .
Voor de inhoud geldt: .
is de straal van de basis;
is de hoogte van de kegel;
is de lengte van het schuine oppervlak, van top tot cirkelrand ;
is de oppervlakte van de platte bodem;
is de oppervlakte van de mantel.
Het lijnstuk wordt ook wel het apothema van de kegel genoemd.
Minimum oppervlakte van een kegel[bewerken | brontekst bewerken]
Van alle denkbare kegels met gelijke inhoud is een kegel met de kleinste oppervlakte de kegel waarvoor geldt dat , waarbij de straal is van de platte bodem. De kegels die congruent aan deze kegel zijn, zijn de kegels, waarvoor het isoperimetrisch quotiënt het grootst is, nl. gelijk aan .
Algemene afleiding[bewerken | brontekst bewerken]
De algemene formule voor de oppervlakte kan worden geschreven als:
In dit geval wordt uitgegaan van een vast volume
- , dus , waardoor
Deze functie heeft een minimum als en dat geldt voor
- zodat
Dit leidt tot
Rekenvoorbeeld[bewerken | brontekst bewerken]
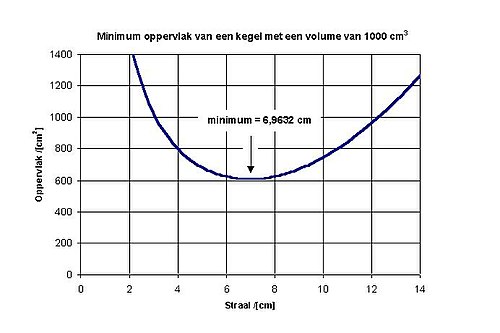
In de grafiek zijn uitgezet welke straal en oppervlakte overeenkomen met een kegel die een inhoud van 1000 cm3 heeft. Voor een kegel met een inhoud van 1000 cm3 geldt:
- ,
waaruit volgt dat
vast is. Hiermee is de kegel met de kleinste oppervlakte te berekenen. Het blijkt, dat de kleinste oppervlakte:
ligt bij cm, zoals de grafiek laat zien. Stralen groter of kleiner dan deze waarde leiden tot grotere oppervlaktes. Uit de minimumwaarde voor valt af te leiden:
Afgeknotte kegel[bewerken | brontekst bewerken]

Een afgeknotte kegel is een lichaam dat ontstaat uit een kegel door tussen de top en het grondvlak een gelijkvormig deel ervan "af te snijden" met een vlak evenwijdig aan het grondvlak.
Zijn en de stralen van het grond- en het bovenvlak en is de hoogte van het lichaam, dan geldt voor de inhoud ervan:
Deze formule is af te leiden uit de inhoud van een regelmatige n-zijdige afgeknotte piramide door de waarde van n onbegrensd te laten toenemen, maar kan ook worden afgeleid door het verschil te nemen van de volumes van de oorspronkelijke kegel en de afgesneden kegel.
Voor de manteloppervlakte van het lichaam geldt:
Hierin is de lengte van het resterend deel van het apothema van de oorspronkelijk kegel.





























