Omwentelingslichaam

Een omwentelingslichaam is een 3D-lichaam dat ontstaat bij het wentelen van een 2D-kromme rond een rechte, die meestal in het vlak van het lichaam ligt.
Wiskundige beschrijving[bewerken | brontekst bewerken]
Een 2D-kromme kan eenvoudig gewenteld worden indien zijn parametervergelijking gekend is: de vector opgebouwd uit de 3 componenten van de parametervergelijking (eventueel aangevuld met een 3d-coördinaat) vermenigvuldigen met een rotatiematrix.
Voorbeeld[bewerken | brontekst bewerken]
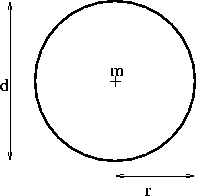
Veronderstel een cirkel C in het xy-vlak, met parametrisering .
- De rotatiematrix voor draaien rond de x-as (=middellijn):
- Het omwentelingslichaam wordt dan , waarbij op te merken valt dat een extra variabele werd toegevoegd, nodig om een oppervlak te beschrijven. Indien de cirkel enkel over 90° gedraaid dient te worden, kan een waarde voor ingevuld worden.
- Het roteren rond de y-as heeft hetzelfde effect.
- Bij het roteren rond de z-as blijft de cirkel in het xy-vlak liggen, iets wat we bewezen zien als we de vergelijking opstellen:
- Zodat er komt.
Analoog kunnen zo de vergelijkingen van onderstaande omwentelingslichamen gevonden worden.
Voorbeelden[bewerken | brontekst bewerken]
Cirkel[bewerken | brontekst bewerken]
Bij het wentelen van een cirkel rond zijn middellijn ontstaat een bol, bij het wentelen rond een rechte buiten de cirkel ontstaat een torus.
Parabool[bewerken | brontekst bewerken]
Bij het wentelen van een parabool rond zijn as, ontstaat een paraboloïde.
Hyperbool[bewerken | brontekst bewerken]
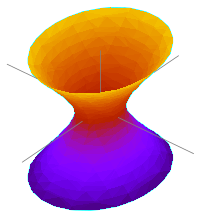
Bij het wentelen van een hyperbool zijn twee mogelijkheden, het wentelen zodat één aaneengesloten stuk ontstaat: eenbladige hyperboloide, en wentelen zodat twee stukken ontstaan, een tweebladige hyperboloide.
Twee rechten[bewerken | brontekst bewerken]
Kruisende rechten[bewerken | brontekst bewerken]
Bij het wentelen van een rechte rond een andere rechte (niet in hetzelfde vlak, dus kruisend), ontstaat een regeloppervlak: een eenbladige hyperboloïde.
Evenwijdige rechten[bewerken | brontekst bewerken]
 Bij het draaien van een rechte rond een andere rechte, die evenwijdig loopt, ontstaat een cilinder.
Bij het draaien van een rechte rond een andere rechte, die evenwijdig loopt, ontstaat een cilinder.
Snijdende rechten[bewerken | brontekst bewerken]
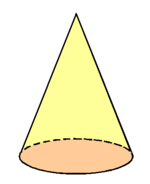 Analoog ontstaat hier een kegel.
Analoog ontstaat hier een kegel.
Door de opbouw is telkens duidelijk dat deze drie voorbeelden een regeloppervlak voorstellen: door ieder punt van het oppervlak gaat een rechte, die volledig tot het oppervlak behoort.
Inhoud en oppervlakte[bewerken | brontekst bewerken]
Inhoud en oppervlakte kunnen worden berekend met een omwentelingsintegraal.
Inhoud[bewerken | brontekst bewerken]

We veronderstellen dat de wentelas de x-as is (de andere gevallen kunnen door roteren veranderen in dit geval); we berekenen de inhoud van het lichaam dat gevormd wordt door het vlakdeel tussen de x-as en , begrensd door x=a en x=b, te roteren rond de x-as:
- .
De inhoud van een cilinder met hoogte b-a=h en straal r is dan : f(x) is namelijk constant, en gelijk aan r.
Oppervlakte[bewerken | brontekst bewerken]
De oppervlakte beschreven door het roteren van een kromme met parametervergelijking rond de x-as is:
Voorbeeld: de oppervlakte van een bol ontstaat door het roteren van een halve cirkel, met vergelijking (t van nul tot π) is dan .
Als we expliciet y kunnen schrijven als een functie van x, dus y = f(x), dan wordt de formule voor de oppervlakte van het omwentelingslichaam bij wentelen om de x-as
Regels van Guldin[bewerken | brontekst bewerken]
De eerste regel van Guldin, vernoemd naar de Zwitserse wiskundige en astronoom Paul Guldin (1577-1643) , stelt dat de oppervlakte van een omwentelingslichaam gelijk is aan de omtrek van de om te wentelen figuur maal de lengte van de cirkel die het zwaartepunt van deze figuur aflegt. De regel kwam al eerder voor in de Synagoge van Pappos van Alexandrië (4e eeuw) en wordt daarom ook wel regel van Pappus genoemd.
De oppervlakte van een torus met omwentelingsstraal van het middelpunt R en straal van de om te wentelen cirkel r is dus
- .
De tweede regel van Guldin stelt dat de inhoud van een omwentelingslichaam gelijk is aan de oppervlakte van de om te wentelen figuur maal de lengte van de cirkel die het zwaartepunt van deze figuur aflegt.
De inhoud van de zojuist beschreven torus kan dus worden gevonden met
- .

![{\displaystyle C(t)=[\cos(t),\sin(t),0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5892759bc5aedee665bb6ec5c9875a961bfe2e04)

![{\displaystyle R_{x}\cdot C(t)=[\cos(t),\sin(t)\cos(\theta ),-\sin(t)\sin(\theta )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e5c8dd0726e2b7b5dadbf3369a3e81215ea62d2)


![{\displaystyle R_{z}\cdot C(t)=[\cos(t)\cos(\theta )+\sin(t)\sin(\theta ),-\cos(t)\sin(\theta )+\sin(t)\cos(\theta ),0]=[\cos(t-\theta ),\sin(t-\theta ),0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3ffe1248bcf89ee875719b7d7dcca0617fce944)








![{\displaystyle [x,y]=[x(t),y(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a69ccb4bf2c697788fa1642dcf20c6f569e9548d)

![{\displaystyle [x,y]=[r\cos(t),r\sin(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3141374dd8687b8a9c7f58cfb3f284f1583f724d)



