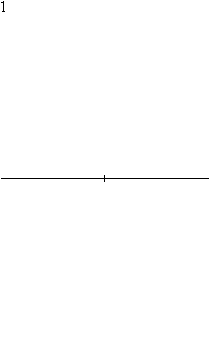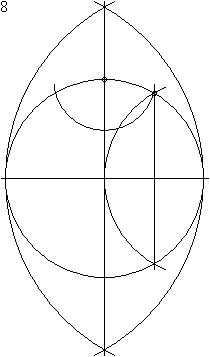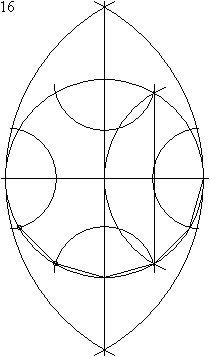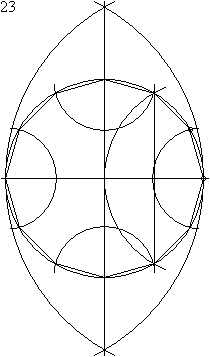Twaalfhoek

Regelmatige twaalfhoek.

Een twaalfhoek of dodecagoon is een figuur met twaalf hoeken en twaalf zijden. Een regelmatige twaalfhoek is een regelmatige veelhoek met twaalf gelijke hoeken en twaalf gelijke zijden. De hoeken van een regelmatige twaalfhoek zijn ($n=12$):

$\alpha ={\frac {(n-2)}{n}}\cdot 180^{\circ }={\frac {10}{12}}\cdot 180^{\circ }=150^{\circ }$

Oppervlakte

De oppervlakte $A$ van een regelmatige twaalfhoek met $a$ de lengte van een zijde is:

${\begin{aligned}A&=3\cot \left({\frac {\pi }{12}}\right)a^{2}=3\left(2+{\sqrt {3}}\right)a^{2}\\&\approx 11{,}19615242\,a^{2}\end{aligned}}$

Als $R$ de straal van de omgeschreven cirkel is, geldt:

$A=6\sin \left({\frac {\pi }{6}}\right)R^{2}=3R^{2}$

Als $r$ de straal van de ingeschreven cirkel is, geldt:

${\begin{aligned}A&=12\tan \left({\frac {\pi }{12}}\right)r^{2}=12\left(2-{\sqrt {3}}\right)r^{2}\\&\approx 3{,}2153903\,r^{2}\end{aligned}}$

Constructie van een regelmatige twaalfhoek

Het construeren met passer en liniaal van een regelmatige twaalfhoek geschiedt in 23 stappen:

Zie ook

• Veelhoek

· ·

Veelhoeken