Vierhoek



Een vierhoek is een meetkundige figuur die uit vier hoekpunten en vier zijden bestaat. Het is op de driehoek na de eenvoudigste veelhoek. De som van de hoeken in de vier hoekpunten van een vierhoek is 360 graden.
Een vierhoek kan al of niet convex zijn. Gelijkwaardige criteria voor convexiteit zijn:
- Het door de vier zijden omsloten gebied is een convexe verzameling.
- Beide diagonalen liggen binnen de vierhoek.
- Voor iedere zijde geldt dat als deze tot een lijn wordt verlengd, de hele vierhoek aan een kant van die lijn ligt.
- Geen van de hoekpunten binnen de driehoek ligt, die door door de andere drie hoekpunten wordt gevormd.
- Geen enkele hoek van de vierhoek is groter dan 180 graden.
Er staat onderaan een diagram met de indeling van de convexe vierhoeken. Een vierhoek die niet convex is, wordt concaaf genoemd. Het is de stelling van Varignon dat de middens van de vier zijden van iedere vierhoek een parallellogram vormen, het parallellogram van Varignon.
Een vierhoek heet ontaard als een van de vier hoeken een gestrekte hoek is. Het omsloten gebied is dan hetzelfde als dat van een driehoek. Een diagonaal valt in dat geval samen met twee zijden.
Convexe vierhoeken[bewerken | brontekst bewerken]
Voorbeelden[bewerken | brontekst bewerken]
- Vierkant - vierhoek met vier gelijke zijden en vier rechte hoeken, het is een regelmatige veelhoek
- Rechthoek - vierhoek met vier rechte hoeken
- Ruit - vierhoek met vier gelijke zijden
- Parallellogram - vierhoek, waarvan de vier zijden twee aan twee evenwijdig zijn
- Trapezium - vierhoek met ten minste twee evenwijdige zijden
- Vlieger - vierhoek met twee paar gelijke aanliggende zijden
Koordenvierhoek[bewerken | brontekst bewerken]
Een koordenvierhoek is een vierhoek waarvan de vier hoekpunten op dezelfde cirkel liggen. De vier zijden zijn dus koorden van deze omgeschreven cirkel. De som van de overstaande hoeken in een koordenvierhoek is 180 graden. Het bewijs hiervan steunt op eigenschappen van middelpunts- en omtrekshoeken. Een rechthoek en een vierkant zijn koordenvierhoeken. Een onregelmatige vierhoek kan een koordenvierhoek zijn en een trapezium alleen als het gelijkbenig is.
Een convexe vierhoek is een koordenvierhoek dan en slechts dan als
Deze eigenschap is de stelling van Ptolemaeus.
Raaklijnenvierhoek[bewerken | brontekst bewerken]
Een raaklijnenvierhoek is een vierhoek waarvan de vier zijden aan dezelfde cirkel raken. De vier zijden zijn dus raaklijnen aan deze ingeschreven cirkel. Als en de lengtes van overstaande zijden zijn en en ook, dan geldt dat . Voor de oppervlakte van een raaklijnenvierhoek geldt: waarbij de omtrek is, dus
en de straal van de cirkel. Vlieger, ruit en vierkant zijn raaklijnenvierhoeken.
Bicentrische vierhoek[bewerken | brontekst bewerken]
Een vierhoek die zowel koordenvierhoek als raaklijnenvierhoek is, heet een bicentrische vierhoek. Een vierkant is een bicentrische vierhoek. Wanneer de straal is van de omgeschreven cirkel, die van de ingeschreven cirkel en de afstand tussen de twee middelpunten van deze cirkels, dan geldt
- .
Vlieger[bewerken | brontekst bewerken]
Een vlieger is een vierhoek waarvan de diagonalen elkaar loodrecht snijden. Als en de lengtes van overstaande zijden zijn en en ook, dan is een vierhoek een vlieger of orthodiagonaal dan en slechts dan als .
Volledige vierhoek[bewerken | brontekst bewerken]
Neemt men vier punten en , waarvan er geen drie op één lijn liggen, met alle zes mogelijke verbindingslijnen, dan wordt deze figuur een volledige vierhoek genoemd. De snijpunten en heten de diagonaalpunten van de volledige vierhoek.
Een volledige vierhoek is een configuratie.
Eigenschappen[bewerken | brontekst bewerken]
- Een lijn door twee diagonaalpunten snijdt de overige zijden in twee punten die ten opzichte van de diagonaalpunten harmonisch liggen.
- De orthopolen van een lijn ten opzichte van de vier driehoeken en liggen op een lijn.
Volledige vierzijde[bewerken | brontekst bewerken]
Neemt men juist vier lijnen, waarvan er geen twee evenwijdig zijn, met alle zes mogelijke snijpunten, dan wordt de figuur een volledige vierzijde genoemd. De drie lijnen tussen hoekpunten die niet al een zijde zijn, heten de diagonalen. De volledige vierzijde is de duale versie van de volledige vierhoek.
Een volledige vierzijde is een configuratie.
Eigenschappen[bewerken | brontekst bewerken]
- De middens van de diagonalen van een volledige vierhoek liggen op een lijn. De dragende lijn wordt de rechte van Gauss genoemd, naar Carl Friedrich Gauss, of de rechte van Newton, naar Isaac Newton. Raakt een kegelsnede aan de vier zijden, dan ligt het middelpunt ervan ook op deze lijn. In het bijzonder ligt het middelpunt van de ingeschreven cirkel van een raaklijnenvierhoek op deze lijn.
- De stelling van Miquel voor een volledige vierzijde zegt dat de omgeschreven cirkels van de vier driehoeken in een volledige vierzijde door een gezamenlijk snijpunt gaan, het punt van Miquel. De vier middelpunten van deze cirkels en het punt van Miquel liggen ook weer op een cirkel.
- De hoogtepunten van de vier driehoeken in een volledige vierzijde liggen op een lijn loodrecht op de rechte van Gauss/Newton.
- De orthopool van een van de lijnen ten opzichte van de driehoek gevormd door de andere drie ligt op deze zelfde lijn van hoogtepunten.
- De orthopolen van een vijfde lijn ten opzichte van de vier driehoeken, die kunnen worden gevormd met de vier lijnen liggen op één lijn.
- De drie cirkels met de diagonalen van een volledige vierhoek als middellijn horen bij dezelfde cirkelbundel. De lijn door de hoogtepunten van de vier driehoeken is de machtlijn van deze cirkelbundel.
- De voetpunten van het punt van Miquel op de vier zijden liggen op één lijn en deze lijn is evenwijdig aan de lijn van de hoogtepunten.
Indeling[bewerken | brontekst bewerken]
| vierhoeken | |||||
|---|---|---|---|---|---|
| ┌─────────────┼─────────────┐ | |||||
| concaaf | convex | zelfdoorsnijdend | |||

|

|

| |||
| ┌─────────────┼─────────────┐ | |||||
|

|
| |||
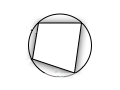
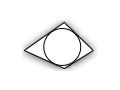
| koordenvierhoek | trapezium | raaklijnenvierhoek met ingeschreven cirkel | |||
| | ┌───────────┤ | | | ||||
 gelijkbenig trapezium |
 parallellogram rotatiesymmetrisch |
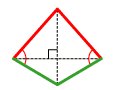 vlieger diagonalen loodrecht | |||
| └─────┬─────┘ | └─────┬─────┘ | ||||
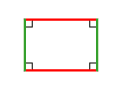 rechthoek rechte hoeken |
 ruit gelijke zijden | ||||
| └──────────┬─────────┘ | |||||
 vierkant | |||||
|


























