Overleg:Zwaartekracht
Onderwerp toevoegenZwaartekrachtgolven longitudinaal of transversaal
[brontekst bewerken]Wat ik me afvraag, zijn zwaartekrachtsgolven longitudinaal of transversaal? Elly 24 sep 2003 14:47 (CEST)
- Eens op het Internet gezocht. Naar wat ik heb gelezen, lijkt het antwoord te zijn: De algemene relativiteitstheorie voorspelt transversale golven, maar er zijn tegenwoordig ook diverse theorieën die beide soorten voorspellen. Zie: http://relativity.livingreviews.org/Articles/lrr-2001-4/node27.html, http://world.std.com/~sweetser/quaternions/sdm.openacs.org/wp/display/916/940.html, http://216.239.59.104/search?q=cache:nsnaqyCG5fAJ:www.thecore.nus.edu.sg/natureslaw/unl2203/gravitational.doc+%22gravitational+waves%22+longitudinal&hl=en&ie=UTF-8, http://www.fh-furtwangen.de/~webers/, http://sepwww.stanford.edu/public/docs/sep75/ray1/paper_html/node3.html Andre Engels 24 sep 2003 15:07 (CEST)
- Dank je, echt interessant! (Sorry, ik had natuurlijk zelf ook ff kunnen zoeken). We moeten maar beter wachten dit te vermelden tot dat ze gedetecteerd zijn. Elly 24 sep 2003 15:18 (CEST)
- Nou, ik denk dat we het wel ongeveer zoals ik het boven zeg kunnen noemen - de algemene relativiteitstheorie is algemeen aanvaard in de natuurkunde, dat geldt voor die andere theorieën niet. Dus zoiets als "Zwaartekrachtsgolven zijn traversaal, al voorspellen sommige theorieën daarnaast ook longitudinale govlen" lijkt me behoorlijk acceptabel vanuit het oogpunt der hedendaagse natuurkunde. Andre Engels 24 sep 2003 15:36 (CEST)
Zwaartekrachtmachine
[brontekst bewerken]Ik heb een vraag die mij al een tijdje bezig houd. Is het op enige manier mogelijk om door middel van een machine of zoiets zwaartekracht te vermeerderen. Dus gewoon iets wat je als grond gebruikt waar je op kunt lopen, maar een grotere aantrekkingskracht heeft dan de aarde zelf. Vincent
Als je in een lift of racket stapt die snel naar boven gaat zal er een kracht op je uitgeoefend worden die groter is dan de zwaartekracht,maar de zwaartekracht zelf wordt niet vermeerderd deze zal zelf lichtjes afnemen.(Kristof vt 4 nov 2004 17:52 (CET)) zo'n simpel toestel voor thuis bestaat dus niet. Wel worden in andere situaties bvb centrifuge krachten opgewekt die groter zijn dan de zwaartekracht.
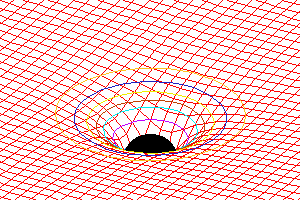
The curvature of spacetime - image
[brontekst bewerken]New image was added to Commons:
Grassprietjes
[brontekst bewerken]Wat ik me afvroeg is : als er zwaartekracht is , waarom staan de grassprietjes dan recht en vallen ze niet om ? Heeft er iemand een antwoord op mijn vraag ?
- Bij mij staan ze niet rechtop, maar vallen ze om!Nijdam 30 mei 2005 23:35 (CEST)
- Combinatie van wortelgestel en turgordruk, vermoed ik (als dit al een serieuze vraag is). Groet, W.D. Sparling (overleg) 4 apr 2012 11:02 (CEST)
Afbeeldingsfout
[brontekst bewerken]Ok geen flauw idee hoe dit werkt , iemand op de afbeelding gelet? een kleinere massa oefent geen even grote kracht uit op een grotere , duh , dat staat juist in de formule onderaan. Wil iemand de vector van de kleine massa verkleinen en de F veranderen in Fz? dat zou veel duidelijk maken. (aangezien bij planeten er een middelpuntzoekende kracht meespeelt ..)

- Afbeelding is prima (als het tenminste gaat over de afbeelding zoals die er nu staat), objecten met verschillende massa trekken elkaar met dezelfde maar tegengesteld gerichte kracht aan, maar door het massaverschil zal de resulterende versnelling voor elk van de twee objecten verschillen. Groet, W.D. Sparling (overleg) 4 apr 2012 11:02 (CEST)
Snelheid van het zwaartekrachtveld
[brontekst bewerken]Dit stukje moet of uitgebreid worden met bronnen, of verhelderd worden. Zoals het er nu staat klopt er iig weinig van. Jupiter heeft geen invloed op het zwaartekrachtveld van wat dan ook buiten ons zonnestelsel. Stbabylon 14 februari 2010 14:14 (CEST)
Zwaartekrachtsgolven
[brontekst bewerken]Zijn het "Zwaartekrachtsgolven" of "Zwaartekrachtgolven"? Ik zou zelf voor het laatste gaan. Het verschil in aantal hits op Google is verwaarloosbaar. Wie o wie weet het antwoord? --Stephan202 28 mei 2006 16:42 (CEST)
- Het huidige groene boekje (formeel nog niet geldig geloof ik) geeft zwaartekrachtSveld. Dus ik zou zeggen, met tussen-s. De regels zijn wat vaag, zie Tussen-s in de Nederlandse spelling. Elly 28 mei 2006 17:12 (CEST)
- Als ik die regels zo lees, dan denk ik dat je gelijk heb. Ik spreek die /s/ wel uit ja. Ik heb het artikel aangepast zodat de tussen-s nu overal aanwezig is. Groeten, Stephan202 28 mei 2006 23:45 (CEST)
Bron van zwaartekracht
[brontekst bewerken]Volgens mij heeft de middelpuntvliedende kracht van hemellichamen de zwaartekracht veroorzaakt. Verrekijker praatjes? 31 dec 2006 00:09 (CET)
Gravitatie vs zwaartekracht
[brontekst bewerken]Op het moment is gravitatie een dp naar zwaartekracht. Ik kan me echter vaag herinneren dat dit niet helemaal gelijk is: zwaartekracht is de resulterende krachtveld bij optelling van zowel het gravitatieveld als het centriputaalveld van de Aarde (dat laatste wordt veroorzaakt door de middelpuntvliedende kracht bij de rotatie van de Aarde). Bij andere hemellichamen zal dit wellicht op dezelfde manier gaan. Iemand hier die dit kan bevestigen? Woudloper 24 mrt 2007 23:18 (CET)
Volgens mij is in het nederlands Zwaartekracht en Gravitatiekracht gewoon synoniem. Dus die dp is wel terecht. Als we ook rekening houden met de draaiing van de aarde dan hebben we het meer over valversnelling. Maar Woudloper heeft wel gelijk dat in het artikel waar die formule staat om g uit te rekenen "in Nederland en België"... daar ontbreekt inderdaad die factor voor de draaiing van de aarde : die formule geldt voor de gravitatiekracht overal op aarde... de "centrifugale" versnelling moet daar nog van afgetrokken worden. Er zijn nog wel andere factoren: de aarde is niet perfect rond en "zeeniveau" is dus niet overal even ver van het midden, en in de aarde is de massa ook niet gelijkmatig verdeeld. Sjoerd22 25 mrt 2007 13:25 (CEST)
- In dat geval staat er ook een fout in Zwaartekrachtsveld. Valversnelling wordt daar uitgelegd als iets dat alleen van de gravitatiekracht afhankelijk is, terwijl als je gelijk hebt ook de centriputaalkracht genoemd zou moeten worden. "Geopotentiaal" (zie de|en) is dacht ik de naam voor de zwaartepotentiaal van een object in het zwaartekrachtsveld van de Aarde. In de Duitse versie (die ik duidelijker vindt dan de Engelse) staat dat dit een optelsom van gravitatie en centriputaalversnelling is. Woudloper 25 mrt 2007 13:56 (CEST)
verplaatst vanuit 'De Kroeg'
[brontekst bewerken]Wellicht hoort deze vraag thuis in het natuurkundecafe, ware het niet dat dat cafe niet bestaat. Zou iemand met verstand van natuurkunde dit eens kunnen doorlezen? Ik ben niet zeker maar het lijkt erop dat er grote fouten zitten in het artikel zwaartekracht. Ik was vanavond bezig iets te schrijven over landmeetkunde/geodesie. Daarvoor gebruik ik de wikipedia van de oosterburen graag als spiekbriefje; ze hebben daar vaak betere technische artikelen dan bij de Engelse vrinden. Op de:Schwerepotential wordt verklaard:
...aus den Kraftfeldern der Massenanziehung (Gravitation) und der Rotation (Zentrifugalkraft) ergibt. Die Schwerkraft ist die Resultierende der beiden o. a. Kräfte und entspricht dem Vertikal-Gradienten des Schwerepotentials.
Samengevat de “Schwerkraft” is een combinatie van de aantrekkingskracht van de massa van een hemellichaam (dit heet in het Duits “Gravitation”) en de centrifugaalkracht veroorzaakt door de rotatie van dat hemellichaam.
In het Duits is er dus een verschil tussen Schwerkraft (zwaartekracht?) en Gravitationkraft (gravitatiekracht?). Op de Nederlandse wikipedia is gravitatiekracht echter een redirect naar zwaartekracht.
Ik zie drie mogelijkheden:
- De redirect op de Nederlandse wikipedia is incorrect: er moet een apart artikel komen over gravitatiekracht.
- De door mij gepleegde vertalingen (met vraagteken) van Schwerkraft en Gravitation kloppen niet.
- De Duitse wikipedia geeft verkeerde informatie.
Ik heb een vermoeden dat het eerste het geval is, omdat de zwaartekracht de kracht is die de valversnelling veroorzaakt (Fz = m g). De valversnelling (g) wordt beschreven met het zwaartekrachtsveld van een hemellichaam, dat (volgens zowel de Nederlandse als Duitse wikipedia) wordt veroorzaakt door de optelsom van de twee krachten (aantrekking van massa en centrifugaalkracht).
Nou is een niet-helemaal-correcte redirect tot daar aan toe, maar kijk eens op zwaartekracht. In dat artikel wordt zwaartekracht beschreven als zijnde... gravitatie. De Duitse wikipedia heeft echter dezelfde info als op nl:zwaartekracht staan in het artikel de:Gravitation. Op de Nederlandse wikipedia is gravitatie echter (net als gravitatiekracht) een redirect naar zwaartekracht. Meest voor de hand liggende conclusie: zowel de info op zwaartekracht als de redirect kloppen niet(?) Wie o wie bevestigt mijn vermoeden? Woudloper 6 jun 2007 02:36 (CEST)
- Gravitatiekracht is de algemene term: tussen ALLE voorwerpen met massa is er wederzijds een aantrekkingskracht. Zwaartekracht gebruikt men vaak specifieker voor die gevallen waar de ene massa enorm groot: typisch bij hemellichamen dus. Als je een appel op de grond laat vallen, dan worden de aarde en de appel naar elkaar toegetrokken ahw, maar de aarde zal niet echt veel bewegen hé, door zijn veel grotere massa. In zo'n gevallen neemt men het woord zwaartekracht eerder aan. Heb je met gelijkwaardige massa's te doen (ttz, in eenzelfde grootte-orde), dan zal men eerder van graviatiekrachten e.d. spreken. En dat alles voor de fysica van Newton, waar je die dingen vaak op een hoopje kunt gooien. Gravitatiekrachten kunnen idd ook een ruimer begrip zijn dan puur de zwaartekracht.
- Hoe men dat formeler en technischer in artikelen invult, giet, of al dan niet onderscheid maakt door opsplitsing, dat laat ik alvast in het midden. --LimoWreck 6 jun 2007 02:42 (CEST)
- Ter aanvulling: zie ook en:Gravitation. In de inleiding vind je een korte uitleg over het engelse onderscheid Gravitation <-> Gravity --LimoWreck 6 jun 2007 02:46 (CEST)
@Limowreck: je bergijpt me verkeerd. Ik heb geen moeite met het verschil tussen gravity (gravitatiekracht) en gravitation (gravitatie), maar tussen gravitatie en gravitatiekracht enerzijds en zwaartekracht anderzijds. Wat er volgens mij blijkt na het vergelijken met de Duitse artikelen is dat zwaartekracht een optelsom van gravitatie en centrifugaalkracht is. In de Nederlandse artikelen staat dat zwaartekracht hetzelfde is als gravitatiekracht (Dat zal op de middelbare school misschien een voldoende nauwkeurige definitie zijn vandaar de fout). Het verschil zit hem er in of de centrifugaalkracht van de Aarde wordt meegerekend. Woudloper 6 jun 2007 10:47 (CEST)
- Klinkt het nu heel erg stom als ik zeg dat de centrifugaalkracht tegengesteld werkt aan de zwaartekracht. M.a.w. als er geen zwaartekracht was en de aarde draaide niettemin rond, dan zouden wij er door die centrifugaalkracht toch juist allemaal afgeslingerd worden in plaats van eraan vast te blijven kleven?
 Thor NLAMAZE ME 6 jun 2007 11:27 (CEST)
Thor NLAMAZE ME 6 jun 2007 11:27 (CEST)
- Bij mijn weten is in het Nederlands (althans in Nederland zelf) het woord "zwaartekracht" volledig equivalent met "gravitatiekracht". Ik zou niet weten hoe de optelsom van gravitatiekracht en centrifugaal"kracht" (da's immers een schijnkracht, hé) in het Nederlands wordt aangeduid. Paul B 6 jun 2007 11:45 (CEST)
- Is het niet duidelijk om "effectieve zwaartekracht" te gebruiken, of zelfs "netto-zwaartekracht", als subkopje onder "zwaartekracht"? Thijs! 6 jun 2007 16:01 (CEST)
- Van Dale (1992) vermeldt bij zwaartekracht dat gravitatie een synoniem is; bij gravitatie staat als eerste betekenis "zwaartekracht" vermeld. Die redirect is correct. Wel een leuk item voor in het artikel - maar die termen verschillende betekenissen geven gaat te ver. Wammes Waggel 6 jun 2007 16:31 (CEST)
- Misschien volstaat een opmerking in de inleiding van het artikel dat de zwaartekracht volgens Newton niet hetzelfde is als de kracht waarmee wij op de aardbodem drukken. Een deel van de zwaartekracht wordt namelijk voor iets anders gebruikt: om ons een cirkelvormige baan om de aardas te laten beschrijven.
- Zo'n kracht die zorgt dat een lichaam een cirkel beschrijft heet centripetaalkracht, of in het Nederlands 'middelpuntzoekende kracht'. Dat is geen kracht die door die baan wordt opgewekt o.i.d. Het is juist een kracht die nodig is om de cirkelvormige baan te veroorzaken.
- Opmerkingen als "dan zouden wij er door die centrifugaalkracht toch juist allemaal afgeslingerd worden" of het gebruik van termen als "de centrifugaalkracht van de Aarde" lijken me daarom misleidend. Dat suggereert dat waar iets draait een uniek soort kracht vrijkomt. De kern van het verhaal is juist dat er kracht vereist is om een lichaam een cirkel te laten beschrijven. In het geval van ons aardbewoners is het de zwaartekracht van de aarde die die arbeid levert. Wat overblijft voelen we als ons gewicht dat op de aardbodem drukt. 'Centrifugaalkracht' of 'middelpuntvliedende kracht' bestaat niet -- of hoogstens als lekenterm om te beschrijven hoe het voelt als je in een draaimolen zit. Zoiets als de 'passagierindestoeldrukkende kracht' van een optrekkende auto. Bart van der Pligt 6 jun 2007 17:28 (CEST)
- Gelukkig maar. Ik voel me opeens weer een stuk vaster op m'n benen staan nu.
 Thor NLAMAZE ME 6 jun 2007 17:44 (CEST)
Thor NLAMAZE ME 6 jun 2007 17:44 (CEST)
- Gelukkig maar. Ik voel me opeens weer een stuk vaster op m'n benen staan nu.
@Wammes Waggel: Van Dale is geen autoriteit op het gebied van Newtons mechanica: ze kunnen het vereenvoudigd of verkeerd hebben. @Thor: als er geen aantrekking van de massa van de Aarde uitging zou je "weggeslingerd" worden door de rotatie idd. @Paul B: kan het woord "zwaartkracht" twee definities hebben? In bepaalde vakgebieden moet er met deze zaken gerekend worden, er zal dan een verschil moeten worden gemaakt tussen de twee. Er moet dan ook een naam voor zijn. @Bart van der Pligt: idd. is er in feite geen centrifugaalkracht. De krachtenbalans is echter op de evenaar anders dan op de pool door de grotere centrifugaalkracht (of zoals jij wilt: grotere hoeveelheid van de zwaartekracht die wordt gebruikt om in de cirkelbeweging te blijven). Dit zorgt ervoor dat de valversnelling aan de evenaar kleiner is. Newtons wet zegt: F = m g. g is valversnelling. De F in die formule is dan iets anders dan alleen de aantrekking van de Aarde, oftewel een andere F dan in Newtons gravitatiewet voorkomt. In het artikel zwaartekracht worden beide wetten gepresenteerd alsof ze over dezelfde kracht gaan. Dat is dan toch fout? In de Duitse versie staat het wel goed, daar zijn er twee artikelen. Woudloper 6 jun 2007 21:47 (CEST)
- Zoals ik al meldde: het lijkt me inderdaad passend om, op welke manier dan ook, op te merken dat het woord zwaartekracht in het Nederlands niet altijd hetzelfde betekent als gravitatie. Gevoelsmatig noemen we de kracht waarmee we op onze ondergrond drukken de 'zwaartekracht'. Als men in sciencefictionfilms een ruimtestation om zijn eigen as laat draaien, zeggen we ook dat dat gebeurt om 'zwaartekracht' op te wekken, terwijl die techniek niets met gravitatie te maken heeft. Ik ben het dus met je eens dat Van Dale zich hier wat makkelijk vanaf maakt. Bart van der Pligt 7 jun 2007 12:42 (CEST)
conventionele kracht
[brontekst bewerken]Wanneer ik google op "conventionele kracht" komt dit artikel bovendrijven. De andere links op de 1ste pagian lijken niet naar een natuurkundig onderwerp te verwijzen. Ik zie het wel als tegenstelling tot nucleaire kracht gebruikt worden. Wat er in dit verband mee bedoeld wordt is me niet duidelijk. Teun Spaans 1 sep 2007 23:31 (CEST)
- Het is mij ook niet duidelijk en betwijfel of het ergens op slaat. Weghalen? --Erwin(85) 2 sep 2007 15:12 (CEST)
- De bedoeling is goed, maar 'conventioneel' is misschien het juiste woord niet. Zwaartekracht trekt aan iedere massa, terwijl andere krachten, zoals de kracht waarmee je een tas optilt of een auto duwt, een bepaald aangrijpingspunt hebben. Volgens Einstein is zwaartekracht een fictie - wie zwaartekracht voelt, ondervindt een versnelling. Dat kan ik begrijpen als je in een versnellend voertuig zit, maar met mijn voeten op de grond is het lastiger te snappen. Handige Harrie 3 sep 2007 12:22 (CEST)
- Het feit dat de zwaartekracht op alle mogelijke stoffen op precies dezelfde manier invloed uitoefent is een van de meest belangrijke argumenten de zwaartekracht als een schijnkracht te zien, niet te onderscheiden van een versnelling. Viridiflavus 12 jan 2010 18:18 (CET)
Gravitatiewet van Newton
[brontekst bewerken]Hoi,
Ik zie in het stukje over de Gravitatiewet van Newton dat men in het voorbeeld de massa in kilogram hanteert. Voor zover ik weet is dit incorrect en dient massa in Newton uitgedrukt te worden. Is er een bewuste reden om in dit voorbeeld kg als eenheid te gebruiken?
- Kilogram is een eenheid van massa, Newton is een eenheid van kracht, dat zijn twee verschillende zaken. Massa in een gewichtloze toestand weegt niets, maar er is nog wel een kracht nodig om te versnellen of te vertragen. Caseman 15 sep 2007 15:31 (CEST)
- Voor zover ik weet is Newton de een eenheid van massa, nog sterker, ik heb altijd geleerd om massa uit te drukken in Newton. Dat massa in het gewichtloze niets weegt ben ik met je eens. Daarom hebben we ook de eenheid Newton uitgevonden he ;-)
- Toch niet, zie de artikelen Massa (natuurkunde) en Kracht. Caseman 15 sep 2007 17:37 (CEST)
- Ik heb even naar je links zitten kijken maar zie ook weer dat ze daar massa in kilogram uitdrukken. Ik ben geen natuurkundige maar snap wel genoeg van bepaalde zaken. Massa is een constante, op het moment dat je massa in kilograms gaat uitdrukken pak je die constante weg. Kilograms zijn maar relatief.
- Hoezo dat nou weer? De lichtsnelheid is ook een constante, en wordt gewoon uitgedrukt in meter per seconde, ander natuurconstantes hebben meestal ook een eenheid (uitgezonderd bijvoorbeeld de Constante van Avogadro). De massa is geen natuurconstante maar de massa van een lichaam is (in de klassieke natuurkunde) wel constant en wordt gewoon in kilogram uitgedrukt. Onder relativistische omstandigheden is de massa trouwens niet constant, maar neemt toe naarmate de snelheid die van het licht nadert. Caseman 15 sep 2007 19:26 (CEST) (wel natuurkundig opgeleid)
- De massa moet inderdaad in kilogram uitgedrukt worden. Massa in Newton heb ik nog nooit van gehoord. Ben je misschien in de war met het uitdrukken van van massa in bijvoorbeeld eV? --Erwin(85) 15 sep 2007 20:34 (CEST)
- Ik denk eigenlijk dat de vraagsteller massa en gewicht door elkaar haalt. Caseman 15 sep 2007 20:52 (CEST)
- De massa moet inderdaad in kilogram uitgedrukt worden. Massa in Newton heb ik nog nooit van gehoord. Ben je misschien in de war met het uitdrukken van van massa in bijvoorbeeld eV? --Erwin(85) 15 sep 2007 20:34 (CEST)
- Hoezo dat nou weer? De lichtsnelheid is ook een constante, en wordt gewoon uitgedrukt in meter per seconde, ander natuurconstantes hebben meestal ook een eenheid (uitgezonderd bijvoorbeeld de Constante van Avogadro). De massa is geen natuurconstante maar de massa van een lichaam is (in de klassieke natuurkunde) wel constant en wordt gewoon in kilogram uitgedrukt. Onder relativistische omstandigheden is de massa trouwens niet constant, maar neemt toe naarmate de snelheid die van het licht nadert. Caseman 15 sep 2007 19:26 (CEST) (wel natuurkundig opgeleid)
- Voor zover ik weet is Newton de een eenheid van massa, nog sterker, ik heb altijd geleerd om massa uit te drukken in Newton. Dat massa in het gewichtloze niets weegt ben ik met je eens. Daarom hebben we ook de eenheid Newton uitgevonden he ;-)
- De eenheid van massa is kg, de eenheid van kracht is N(ewton). 1 N is equivalent met 1 kg.m/s2, af te leiden uit F = m.a. De massa van een object is inderdaad een constante, ongeacht of die zich op aarde of op de maan bevindt. Het gewicht is echter wel afhankelijk daarvan, op aarde weeg je meer dan op de maan. Helaas wordt gewicht, eigenlijk de kracht uitgeoefend door de zwaartekracht van een hemellichaam op een massa, uitgedrukt in kg, terwijl het eigenlijk N zou moeten zijn. Viv3210
BTW, zover ik weet (kan me vergissen) verandert het gewicht niet bij relativiteit, alleen het waargenomen gewicht door een waarnemer die niet meebeweegt met de massa. Viv3210
- Laten we er gewoon van uitgaan dat Newton nog geen enkel idee had van relativistische verschijnselen, en daar ook zijn wet op baseerde. Dat de massa toeneemt bij snelheden die de lichtsnelheid benaderen hebben we aan Albert Einstein te danken, je voegt energie aan iets toe en dat uit zich in een toename van de massa volgens E=mc2. Caseman 24 feb 2010 09:30 (CET)
- Ja natuurlijk had Newton daar nog geen idee van, maar wat ik bedoelde is dat de massa van het bewegende voorwerp voor de waarnemer die meebeweegt niet zal veranderen (gezien de relativiteitstheorie het heeft over de gelijkwaardigheid van waarnemers). Viv3210
- Laten we er gewoon van uitgaan dat Newton nog geen enkel idee had van relativistische verschijnselen, en daar ook zijn wet op baseerde. Dat de massa toeneemt bij snelheden die de lichtsnelheid benaderen hebben we aan Albert Einstein te danken, je voegt energie aan iets toe en dat uit zich in een toename van de massa volgens E=mc2. Caseman 24 feb 2010 09:30 (CET)
Gravitatie
[brontekst bewerken]Gravitatie is een ander woord voor zwaartekracht. De term 'gravitatiekracht', die wel door sommigen gehanteerd wordt, en ook in het artikel staat, betekent dus 'zwaartekrachtkracht. Willen we dat? Madyno 11 jun 2009 00:45 (CEST)
- Lijkt me op zich niet zo erg, "zwaartekracht" ofwel "gravitatie" als begrip gaat over een krachtveld, en de zwaartekrachtkracht is de kracht die op een lichaam uitgeoefend wordt als resultaat van dat krachtveld. Alleen taalkundig staat het een beetje raar als je het zo uitschrijft. "Zwaartekrachtveldkracht" zou m.i. beter zijn, maar klinkt nog steeds krom. Caseman 24 feb 2010 09:36 (CET)
Theorie versus Wet
[brontekst bewerken]Overal in dit artikel gaat het over de zwaartekrachttheorie van Newton. Dit is onjuist, het is geen theorie die hij beschreef, maar een wet, door hemzelf omschreven als 'Newton's law of universal gravitation'. Er zou dus '(Newtons) wet van de zwaartekracht' moeten staan. Pas later (in 1905) is deze wet vervangen door Einsteins relativiteitstheorie. Zodoende vind ik dat dus alle verwijzingen naar Newtons wet waar 'theorie' staat, deze vervangen moet worden in 'wet'. --Guuskeee 25 mei 2010 16:22 (CEST)
Hou er rekening mee dat er geen 'wet' bestaat dat de heer Newton zijn titel de zwaartekracht is tot op heden nooit herhaaldelijk bewezen dus kan er geen sprake zijn van een 'wet'(Maus). – De voorgaande bijdrage werd geplaatst door 83.162.221.147 (overleg · bijdragen) 9 jan 2018 21:57 (CET)
- In deze context kun je "law" niet zondermeer vertalen in "wet". Afgezien daarvan wordt de vertaling bemoeilijkt doordat Newton zo lang geleden leefde en de stand van de filosofie een andere was. Tegenwoordig wordt het begrip "wet" in de natuurkunde in academische kringen niet of nauwelijks meer gebruikt. In schoolboeken, populaire wetenschappelijke teksten en amerikaanse teksten wordt het wel gebruikt.
- In hedendaagse taal kun je dus spreken over Newtons theorie. Zwitser123 (overleg) 10 jan 2018 10:26 (CET)
zwaartekracht, een puur kwantummechanisch verschijnsel
[brontekst bewerken]In 2003 kwam Vasily Yanchilin in zijn boek The Quantum Theory of Gravitation met een kwalitatieve verklaring van de zwaartekracht, gebaseerd op de stelling dat massa de Heisenberg onzekerheid reduceert en uitgewerkt volgens het algemeen erkende principe van least action. In het kort: Stel dat een massa zich op x=0 bevindt en een zeer klein deeltje op x=10. Onderhevig aan de Heisenberg onzekerheid zal dit deeltje een volgend ogenblik op x=9,9999.... kunnen zijn. Hier is er grotere bepaaldheid, geringere Heisenberg onzekerheid, zodat transities terug minder vaak voor komen. Netto is er dan beweging richting die externe massa. Dat heet in gewone taal aantrekking door de zwaartekracht. Hieraan voeg ik toe dat we die verspringingen zeg ieten kunnen noemen -wellicht enigszins vergelijkbaar met snaren in andere theorieen- zodat bekende woorden als bijvoorbeeld electron voor het geheel te gebruiken blijven. Er gaan dan meer ieten van x=10 naar x=9,999.... dan omgekeerd en het electron schuift op naar de externe grote massa. In die massa zullen eveneens ieten druk bezig zijn maar het netto resultaat is nul (afgezien van de minieme aantrekkingskracht van het kleine deeltje). Geef je een duw aan die massa dan verandert de balans en krijg je te maken met inertiele massa. In de algemene relativiteitstheorie van honderd jaar geleden wordt gravitatie-massa equivalent gesteld aan inertiele massa. In de nieuwe theorie echter constitueert gravitatie-massa het heelal en veranderen lichtsnelheid en Planck als gevolg van afnemende potentiaal der totale masasa door uitdijing van het universum. In een inertieel stelsel daarentegen veranderen de lichtsnelheid en de Planck niet. De afname van de voortplantingssnelheid der electro-magnetische golven vergt correctie van de info verkregen van supernovae Ia en maakt negatieve energie, inflatie, de cosmologische constante overbodig. Nu een vraag: Vergelijk dat verspringen volgens Heisenberg even met trillen. Een electron kan door twee gaten tegelijk ofwel zullen er bij wijze van spreken ieten door het ene en ieten door het andere gat gaan. Bij grotere objecten is er evenwel geen sprake van een vage, trillende rand en u neemt het ding waar als volkomen in rust. Extrapoleer vervolgens en verduidelijk of hiermee wordt ondersteund de bovengenoemde stelling dat massa de Heisenberg onzekerheid reduceert. (Yanchilin heeft onlangs een manuscript over pro en contra van zwarte gaten voltooid en zoekt daarvoor een uitgever. Wellicht dat daarin nieuwe info gepresenteerd wordt). Scrit: Jitso Keizer www.janjitso.blogspot.com – De voorgaande bijdrage werd geplaatst door 130.37.91.178 (overleg · bijdragen) 29 jul 2011 11:17
23 augustus 2011 Uit het boek van Vasily Yanchilin, pag 63: Beschouw een wolk van elementaire deeltjes. Door de zwaartekracht krimpt de wolk, de deeltjes trekken elkaar aan. Dan nemen de snelheden van deze deeltjes toe. Indien de restmassa's van de deeltjes hetzelfde zou blijven zullen de inerte massa's toenemen als gevolg van de grotere snelheden. Maar dan neemt de inertie van de hele wolk toe en dat is onmogelijk. De nieuwe theorie behelst dat de onbepaaldheid a la Heisenberg toeneemt naarmate er verder van massa verwijderd is. In het verleden was het heelal kleiner en aan de randen toen zal die onbepaaldheid groot geweest zijn, terwijl de snelheid van fotonen er sterk afnam. Te onderzoeken is of hier een bron van donkere materie gelegen kan zijn. Een nog kortere samenvatting van de nieuwe zwaartekrachtstheorie: Twee deeltjes hebben in hun dichtstbijzijnde helften een iets grotere bepaaldheid volgens de Heisenberg relatie dan in de verst verwijderde helften, zodat netto er een klein positief verschil in transities naar elkaar toe ontstaat. – De voorgaande bijdrage werd geplaatst door 130.37.91.199 (overleg · bijdragen) 23 aug 2011 13:33
Nieuwe meetbare effecten
[brontekst bewerken]zie Testing the Strong Equivalence Principle: Detection of the External Field Effect in Rotationally Supported Galaxies. Als een stuk in Donkere materie.Smiley.toerist (overleg) 20 dec 2020 01:54 (CET)
Notatie volume-element
[brontekst bewerken]Is het wel gangbaar en duidelijk om een volume-element aan te geven met ? - Patrick (overleg) 11 jan 2022 18:24 (CET)
- Nee, moet er nog aan werken. Madyno (overleg) 11 jan 2022 19:13 (CET)
Zwaartekracht is geen bewezen kracht
[brontekst bewerken]Newton publiceerde in 1687 een hypothese aan de hand waarvan hij allerlei verschijnselen kon verklaren en voorspellen met behulp van slechts één grondregel. Hij postuleerde daarbij het bestaan van zwaartekracht. Newton's hypothese is een zeer werkbare gebleken. Met behulp ervan kunnen berekeningen en betrouwbare voorspellingen worden gegeven die het alledaagse leven sterk vergemakkelijken. Maar het bestaan van zwaartekracht is geen feit, en Einstein heeft laten zien dat de beschreven verschijnselen ook goed te verklaren zijn door aan te nemen dat een massa de tijdruimte eromheen kromt. Als ik ons artikel lees, dan krijg ik toch vooral een tekst onder ogen die de zwaartekracht als een feit presenteert. En dat is onterecht. Ik heb echter geen zin om dat in m'n eentje te gaan aanpakken. Wie doet hier een voorzet? WIKIKLAAS overleg 30 mei 2023 18:28 (CEST)
- Ik vind dit meer een filosofisch punt. Wat is een feit? Zwaartekracht bestaat wel degelijk, of je nu dit als een kracht of een kromming van de tijdruimte beschouwd. Deze laatste theorie zal in sommige toepassingen nauwkeurig zijn. De Middelpuntvliedende kracht is een schijnkracht maar een lokale waarnemer zal er geen verschil vinden met de zwaartekracht (ook tijd relativiteitseffecten), alleen als die beweegt kan de waarnemer wel Corioliseffecten ondervinden.Smiley.toerist (overleg) 30 mei 2023 18:47 (CEST)
- Kracht is versnelling. Er is overweldigend empirisch bewijs dat Newton die correct beschreef. Hij gaf geen causale verklaring (hypotheses non fingo). Lorentz/Einstein wel. Maar zo'n verklaring kan als zodanig niet bewezen worden, alleen begrepen :o). MWAK (overleg) 1 jun 2023 16:08 (CEST)
Getijden op de maan ?
[brontekst bewerken]Moet je om over een getijdenveld te praten niet eerst een getij hebben ? Sjoerd22 (overleg) 11 jun 2023 14:15 (CEST)
- Je kan geen getij op de maan hebben, daar de maan altijd hetzelfde oppervlakte aan de aarde laat zien. Synchronisatie van draaisnelheid (dag) met de baan om de aarde.Smiley.toerist (overleg) 11 jun 2023 14:22 (CEST)
- De klopt helemaal.....plus het niet onbelangrijke punt dat er op de maan geen water is !! Sjoerd22 (overleg) 11 jun 2023 15:00 (CEST)
- Getijdenkrachten werken ook op het niet vloeibare deel van een hemellichaam. Dit kan hemellichamen opwarmen en vulkanisme veroorzaken. In extreem gevallen kunnen getijdenkrachten uit een hemellichaam opbreken. Volgens sommige theorieën zou er in de diepste permanente schaduwen ijs voorkomen op de maan. De waterstof uit de zonnewind zou dan combineren met de zuurstof uit de gesteenten op de maan.Smiley.toerist (overleg) 12 jun 2023 12:18 (CEST)
- De klopt helemaal.....plus het niet onbelangrijke punt dat er op de maan geen water is !! Sjoerd22 (overleg) 11 jun 2023 15:00 (CEST)

