In de multivariabele analyse, een deelgebied van de wiskunde, is een partiële afgeleide van een functie van een aantal variabelen, de afgeleide waarbij alleen een van de variabelen daadwerkelijk als variabele wordt behandeld en de andere als constanten. Partiële afgeleiden worden in de differentiaalmeetkunde en de vectoranalyse gebruikt. De partiële afgeleide wordt dus per definitie langs de richting van een van de coördinaatassen bepaald.
Neemt men bijvoorbeeld van de functie

de partiële afgeleide naar  , dan wordt de variabele
, dan wordt de variabele  als constante behandeld. De constante
als constante behandeld. De constante  blijft natuurlijk altijd constant. Hieruit volgt:
blijft natuurlijk altijd constant. Hieruit volgt:

De partiële afgeleide van een functie  met betrekking tot de variabele
met betrekking tot de variabele  wordt op verschillende manieren aangeduid. Om het onderscheid te maken met de gewone afgeleide gebruikt men het ronde partiële-afgeleidesymbool
wordt op verschillende manieren aangeduid. Om het onderscheid te maken met de gewone afgeleide gebruikt men het ronde partiële-afgeleidesymbool  in plaats van
in plaats van  men noteert:
men noteert:
 of
of 
Het partiële-afgeleidesymbool  werd geïntroduceerd door Adrien-Marie Legendre (1752 - 1833), raakte vervolgens op de achtergrond, maar won na de herintroductie van dit symbool door Carl Jacobi (1804 - 1851) algemene aanvaarding.[1]
werd geïntroduceerd door Adrien-Marie Legendre (1752 - 1833), raakte vervolgens op de achtergrond, maar won na de herintroductie van dit symbool door Carl Jacobi (1804 - 1851) algemene aanvaarding.[1]
De richtingsafgeleide is een generalisatie van de partiële afgeleide en is de afgeleide van de functie in een gegeven richting. Partiële afgeleiden kunnen voor functies in een scalair veld worden bepaald, maar ook voor functies in een vectorveld. Dat geldt voor de richtingsafgeleiden dus hetzelfde. De richting in een scalair veld waarin de richtingsafgeleide het grootst is, is de gradiënt van het scalaire veld. Dat is in ieder punt in het scalaire veld, dus in het hele scalaire veld. De gradiënt wordt ook wel eens de richtingsafgeleide genoemd.
Grafiek van

en de corresponderende
raaklijn door het
punt 
evenwijdig aan het
xz-vlak.
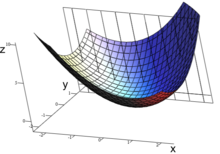
Stel dat  een functie is van twee variabelen. Bijvoorbeeld,
een functie is van twee variabelen. Bijvoorbeeld,

De grafiek van deze functie definieert een oppervlak in de euclidische ruimte. Er is voor ieder punt op het oppervlak in iedere richting een raaklijn. Partieel differentiëren is de handeling om een van deze raaklijnen te kiezen en de richtingscoëfficiënt daarvan te vinden. De raaklijnen kunnen bijvoorbeeld zo worden gekozen dat zij evenwijdig aan het  -vlak of aan het
-vlak of aan het  -vlak lopen.
-vlak lopen.
Om de richtingscoëfficiënt van de raaklijn aan de functie op  te vinden, die evenwijdig aan het
te vinden, die evenwijdig aan het  -vlak loopt, wordt de variabele
-vlak loopt, wordt de variabele  als een constante behandeld. Door de afgeleide van de vergelijking te vinden, onder de veronderstelling dat
als een constante behandeld. Door de afgeleide van de vergelijking te vinden, onder de veronderstelling dat  constant is, vindt men dat de richtingscoëfficiënt van
constant is, vindt men dat de richtingscoëfficiënt van  in het punt
in het punt  gelijk is aan:
gelijk is aan:

Door substitutie in punt  vindt men dat de richtingscoëfficiënt in dit punt gelijk is aan 3.
vindt men dat de richtingscoëfficiënt in dit punt gelijk is aan 3.

Dat wil zeggen dat de partiële afgeleide van  met betrekking tot
met betrekking tot  in het punt
in het punt  gelijk is aan 3.
gelijk is aan 3.
De partiële afgeleide van de functie  , als functie van de variabelen
, als functie van de variabelen  , naar de variabele
, naar de variabele  is:
is:

Hierin staat lim voor de limiet.
De richtingsafgeleide is de afgeleide langs een willekeurige, maar vaste richting.
De partiële afgeleiden,  en
en  van de functie
van de functie  zijn vaak zelf functies van
zijn vaak zelf functies van  en
en  We zouden deze functies nogmaals partieel kunnen differentiëren naar
We zouden deze functies nogmaals partieel kunnen differentiëren naar  of
of  . Hierdoor ontstaan vier partiële afgeleiden van de tweede orde:
. Hierdoor ontstaan vier partiële afgeleiden van de tweede orde:




Volgens de stelling van Schwarz zijn de laatste twee termen gelijk aan elkaar indien  ,
,  en
en  bestaan en continu zijn. In dat geval geldt dus
bestaan en continu zijn. In dat geval geldt dus

Zij  gegeven door
gegeven door  . Dan geldt:
. Dan geldt:

De variabele  wordt hier als constante gezien en naar de variabele
wordt hier als constante gezien en naar de variabele  gedifferentieerd. Op dezelfde manier is:
gedifferentieerd. Op dezelfde manier is:

 wordt hier als een constante gezien.
wordt hier als een constante gezien.
Voor de tweede partiële afgeleide  geldt:
geldt:

dus

We onderzoeken de volgende functie:


Hier wordt met  gerekend alsof het een constante was
gerekend alsof het een constante was

 wordt hier constant gehouden.
wordt hier constant gehouden.
Er zijn in de wiskunde matrices gedefinieerd, waarvan alle elementen partiële afgeleiden zijn.
- Hessiaan - met alle mogelijke partiële afgeleiden van de tweede orde in een scalaire ruimte
- Jacobi-matrix - met alle mogelijk partiële afgeleiden voor een functie in een vectorruimte