Renormalisatie
Renormalisatie is een techniek die wordt gebruikt in de kwantumveldentheorie en in de statistische mechanica als een continue limiet moet worden genomen en bepaalde grootheden oneindige waarden zouden aannemen
Als men tijd en ruimte beschrijft als een continuüm, gebeurt het vaak dat bepaalde statistische of kwantummechanische constructies slecht gedefinieerd zijn. Hierom moeten limieten met zorg worden genomen. Renormalisatie bepaalt dan de relatie tussen de parameters van de theorie, als de parameters bij afstanden op grote schaal verschillen van de parameters bij afstanden op kleine schaal.
Renormalisatie is oorspronkelijk ontwikkeld in de kwantumelektrodynamica (QED) om een zin te geven aan de divergente integralen in de perturbatietheorie. Oorspronkelijk werd deze techniek als verdacht beschouwd door enkele van haar bedenkers, maar uiteindelijk is ze algemeen aanvaard als een belangrijk en zelfconsistent deel van verscheidene gebieden in de natuurkunde en in de wiskunde.
Zelfinteracties in de klassieke natuurkunde[bewerken | brontekst bewerken]
Het probleem van oneindigheden werd voor het eerst tegengekomen in de klassieke elektrodynamica van puntdeeltjes in de 19e en vroege 20e eeuw.
Het elektrische veld van een elektron bevat elektrostatische energie, en door de equivalentie tussen massa en energie zou dit veld bijdragen tot de effectieve massa van het elektron. Nu is de energie van het veld rond een geladen holle sfeer van lading en met straal gelijk aan
Als een elektron wordt beschouwd als een puntdeeltje, is , en wordt de energie oneindig.
De totale effectieve massa van het elektron bestaat uit de som van de massa zonder de elektrische energie (de "naakte" massa) plus de bijdrage van het elektrische veld. Door te postuleren dat de naakte massa negatief is, zou het mogelijk worden ervoor te zorgen dat de limiet voor op de juiste waarde uitkomt. Dit wordt renormalisatie genoemd, en Lorentz en Abraham hebben hier een klassieke theorie van het elektron op gebaseerd. Dit vroege werk vormde de inspiratie voor latere pogingen tot regularisatie en renormalisatie van kwantumveldentheorieën.
Als men elektromagnetische interacties van geladen deeltjes berekent, is het verleidelijk de terugslag van het veld van het deeltje zelf te negeren. Deze terugslag is nodig om de wrijving te verklaren die een geladen deeltje ondervindt bij het uitstralen van straling. Indien een elektron een punt wordt verondersteld te zijn, zal de waarde van de terugslag divergeren om dezelfde reden als waarom de massa divergeert: het veld dicht bij het elektron wordt onbeperkt groot.
De Abraham-Lorentzkracht bevatte een niet-causale "voorversnelling". Soms zou een elektron beginnen met bewegen vóórdat er enige kracht op inwerkt. Dit is een teken dat de puntlimiet niet consistent is. Een lichaam met eindige grootte zal beginnen bewegen als een kracht wordt uitgeoefend binnen één straal van het massamiddelpunt.
Het probleem was erger in klassieke veldentheorie, dan in kwantumveldentheorie, omdat een geladen deeltje in kwantumveldentheorie kan fluctueren in een antideeltje. Dit antideeltje heeft een tegengestelde lading, en de fluctuaties worden uitgesmeerd over een gebied met grootte van ongeveer de comptongolflengte. In kwantumelektrodynamica zal, bij voldoende kleine koppeling, de elektromagnetische massa slechts zoveel divergeren als de logaritme van de straal van het deeltje. Heel wat fysici geloven dat, indien de fijnstructuurconstante veel groter was dan één en de klassieke elektronstraal groter is dan de kwantummechanische golflengte, dezelfde problemen van de klassieke theorie nog steeds in de kwantumversie zullen optreden.
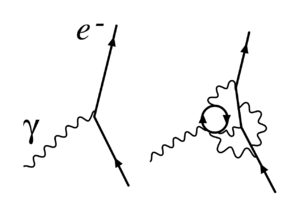
Divergenties in kwantumelektrodynamica[bewerken | brontekst bewerken]
Toen de kwantumelektrodynamica werd ontwikkeld in de jaren dertig, ontdekten Born, Heisenberg, Jordan en Dirac dat heel wat integralen in de perturbatiereeks divergeerden.

Stueckelberg en later ook Schwinger, Feynman en Tomonaga vonden een manier om deze divergenties te beschrijven, die wat later werd gesystematiseerd door Dyson. De divergenties komen voor in berekeningen met Feynmandiagrammen waarin gesloten lussen van virtuele deeltjes voorkomen.
Hoewel virtuele deeltjes aan de wetten van behoud van impuls en energie gehoorzamen, zijn hun energie en impuls willekeurig en kunnen ze zelfs waarden aannemen die niet in overeenstemming zijn met hun massa (zodat niet gelijk is aan ). Zulke deeltjes heten off-shell te zijn. Wanneer virtuele deeltjes in een reactie een lus vormen, wordt de impuls in deze lus niet meer uniek bepaald door de inkomende en uitgaande deeltjes. Zo zal elk verandering van impuls van één deeltje in de lus exact kunnen worden gecompenseerd door de andere deeltjes in de lus, zodat de nodige behoudswetten nog steeds blijven gelden. Om de volledige bijdrage van het diagram te vinden, moet worden geïntegreerd over álle mogelijke combinaties van energie en impuls die in de lus kunnen stromen. Deze integralen zijn vaak divergent — ze geven oneindig als resultaat.
Er zijn nu twee soorten divergenties:
- Infrarood-divergenties: treden op als de integralen in kwestie divergent zijn voor kleine energie en impuls. Dit kan gebeuren als massaloze deeltjes (zoals fotonen) optreden. Elk proces waarbij geladen deeltjes en rol spelen, gaat gepaard met het uitzenden van oneindig veel coherente fotonen van oneindige lange golflengte (dus oneindig kleine energie). Bij fotonen zijn deze divergenties goed verstaan en leveren ze geen grote problemen.
- Ultraviolet-divergenties: treden op als de integralen in kwestie divergeren voor grote energie en impuls. Deze moeten, op de een of andere manier, worden geregulariseerd en gerenormaliseerd voordat enige zinnige informatie uit de berekening kan worden gehaald.

Gerenormaliseerde en naakte grootheden[bewerken | brontekst bewerken]
Een belangrijk feit in renormalisatie is dat de grootheden die voorkomen in de theoretische formules (zoals de uitdrukking voor de Lagrangiaan) en die dingen voorstellen als de elektrische lading en massa van het elektron, niet daadwerkelijk de grootheden zijn die men in een laboratorium meet. De grootheden zoals men ze neerschrijft zijn "naakte" grootheden —de grootheden zonder rekening te houden met de bijdragen van lussen van virtuele deeltjes. De effecten van loops bevatten onder andere de interacties van de elektronen met zichzelf —diezelfde interactie die in de klassieke theorie voor elektromagnetisme net zo moeilijk te behandelen was. In het algemeen zullen deze effecten net zo hard divergeren als de dingen die men wil bestuderen. Hierom impliceren eindige gemeten grootheden oneindige naakte grootheden.
Om de link te leggen met de werkelijkheid, moeten de formules worden herschreven in termen van de meetbare, "gerenormaliseerde" grootheden. Zo zal men, bijvoorbeeld, de lading van het elektron definiëren bij een zeker renormalisatie- of subtractiepunt (dat meestal wordt gegeven door een zekere energieschaal te specifiëren, en die dus ook vaak renormalisatieschaal wordt genoemd). Het verschil tussen de naakte en de gerenormaliseerde Lagriangiaan kan dan worden afgezonderd en wordt geïnterpreteerd als tegentermen die divergeren en die de divergenties in loopdiagrammen opheffen.
Running van constanten[bewerken | brontekst bewerken]
Bij het hele procedé van renormalisatie, moet men een energieschaal kiezen. In theorie is deze schaal willekeurig en zullen de exacte resultaten van de hele perturbatiereeks niet van de schaal afhangen. In de praktijk berekent men echter slechts de eerste termen van de reeks, en in dat geval geeft de benadering de beste resultaten indien de schaal dicht bij de energieën en impulsen van de interactie wordt gekozen.
De effectieve parameters van de theorie hangen af van de schaal die wordt gekozen, zodat het waargenomen gedrag van de theorie afhangt van de interactie waarbij men haar bestudeert. De variatie van de parameters met de energie wordt beschreven door de renormalisatiegroep.
De koppelingsconstante van kwantumchromodynamica wordt, bijvoorbeeld, kleiner bij hogere energie. Dit zorgt ervoor dat, indien quarks worden onderworpen aan zeer hoog-energetische botsingen, dat ze nauwelijks met elkaar zullen interageren. Dit noemt men asymptotische vrijheid. In theorie zou men dezelfde interactie kunnen beschrijven door een lagere renormalisatieschaal te gebruiken, maar in dat geval zal de zwakte van de interactie pas tot uiting komen door het tegen elkaar wegvallen van een heleboel Feynmandiagrammen uit de perturbatiereeks.
Regularisatie[bewerken | brontekst bewerken]
Essentieel komt renormalisatie erop neer het verschil te nemen tussen twee divergente grootheden. Aangezien oneindig min oneindig niet bepaald is, moeten de oneindigheden eerst worden "getemd". De conceptueel eenvoudigste manier is door te bepalen dat alle impulsen en energieën boven een zekere cut-off niet meedoen. Dan kan men de berekeningen voortzetten (er zijn geen oneindigheden), en aan het eind van de berekening neemt men de limiet .
Deze werkwijze kan worden geïnterpreteerd als het feit dat de exacte natuurkundige wetten bij hoge energie niet noodzakelijk die zijn die wij kennen, maar dat de ons bekende wetten slechts benaderingen zijn. Dat betekent dat we in berekeningen niet hoger mogen gaan dan een zekere energie , aangezien we niet weten wat daarboven zit. Maar aangezien ongetwijfeld een zeer grote waarde heeft (of we zouden de "nieuwe fysica" érgens wel al hebben opgemerkt), nemen we aan het eind de limietwaarde. Indien de natuurkunde "af" was, dan zouden we de wetten kennen tot op oneindig hoge energie en zouden we ongetwijfeld nooit divergenties vinden.
Er bestaan echter ook andere manieren om divergente grootheden te regulariseren, elk met haar eigen voor- en nadelen. Een tegenwoordig veelgebruikte techniek is dimensionale regularisatie, uitgevonden door 't Hooft en Veltman. Deze houdt in dat het aantal dimensies van de ruimtetijd wordt gelijkgesteld aan een willekeurig complex getal. Aan het eind van de berekeningen neemt men dan de limiet van het aantal dimensies naar vier. Een andere manier is Pauli-Villarsregularisatie, waarbij fictieve deeltjes aan de theorie worden toegevoegd op een zodanige manier dat de divergenties veroorzaakt door deze deeltjes die van de echte deeltjes opheffen.
Een ander belangrijk regularisatieschema is roosterregularisatie, ingevoerd door Wilson. Hierbij wordt de ruimtetijd vervangen door een rooster van punten met een zekere roosterafstand . Deze lengteschaal zorgt voor een natuurlijke cut-off doordat deeltjes met te hoog momentum niet meer op de rooster kunnen propageren. Aan het eind van de berekeningen moet men dan uiteraard de continuümlimiet nemen. Roosterregularisatie wordt vooral gebruikt in computersimulaties.
Renormaliseerbaarheid[bewerken | brontekst bewerken]
Nu is het zo dat niet alle theorieën kunnen worden gerenormaliseerd. Het kan bijvoorbeeld gebeuren dat het invoeren van tegentermen om divergenties te neutraliseren, leidt tot nieuwe divergenties, die nieuwe tegentermen eisen, en zo voorts. Het eindresultaat is dan een theorie met oneindig veel parameters, en elke waarnemen zou van al deze parameters afhangen. Voordat men de theorie kan testen, moeten eerst alle parameters worden bepaald, wat onmogelijk is. Zulk een theorie is dus helemaal waardeloos en wordt "niet-renormaliseerbaar" genoemd.
Het Standaardmodel van de deeltjesfysica bevat enkel renormaliseerbare interacties, maar de algemene relativiteitstheorie wordt niet-renormaliseerbaar indien men haar kwantiseert op de meest voor de hand liggende manier. Dit suggereert dat perturbatietheorie niet werkt voor kwantumzwaartekracht.
In de effectieve veldentheorie, echter, is "renormaliseerbaarheid" een onaccurate benaming. In een niet-renormaliseerbare effectieve veldentheorie zijn er inderdaad oneindig veel termen, maar hun coëfficiënten bevatten steeds negatievere machten van de cut-off. Indien deze een echte, fysische grootheid is, dan beschrijven deze oneindig veel tegentermen fysische interacties. Indien de energieën van de interacties niet groot worden, kan men berekeningen ontwikkelen in inverse machten van de cut-off om tot benaderde resultaten te komen op basis van een eindig aantal parameters.
De niet-renormaliseerbare interacties in een effectieve veldentheorie worden snel zwakker als de energieschaal veel kleiner wordt dan de cut-off. Het klassieke voorbeeld is de theorie van Fermi van de zwakke kernkracht. Dit is een niet-renormaliseerbare effectieve veldentheorie waarvan de cut-off van de orde is van de massa van het W-boson. Indien men experimenten doet bij de schaal van de cut-off, is de Fermi-interactie niet meer bruikbaar en moet men overgaan op de volledig theorie: de elektro-zwakke theorie.
Deze kijk verklaart ook waarom bijna alle fundamentele interacties die wij kennen, worden beschreven door renormaliseerbare theorieën. Het zou kunnen dat er andere interacties bestaan die niet-renormaliseerbaar zijn, maar dat zij slechts een rol beginnen te spelen bij, bijvoorbeeld, de Planckschaal. Hierdoor merken wij er niets van. De uitzondering is zwaartekracht, die ongelooflijk zwak is, maar toch merkbaar doordat de gigantische massa's van de hemellichamen het effect ervan versterken.
Meningen en interpretatie[bewerken | brontekst bewerken]
De pioniers van QED en van kwantumveldentheorie in het algemeen waren veelal ontevreden met de situatie zoals ze was. Het leek hen niet werkelijk toegestaan oneindigheden van elkaar af te trekken om eindige resultaten te krijgen. Dirac was bijvoorbeeld een van de grote tegenstanders:[1]
- De meeste fysici zijn heel tevreden met de situatie. Ze zeggen: 'Kwantumelektrodynamica is een goede theorie en we hoeven ons er geen zorgen meer over te maken.' Ik moet zeggen dat ik zeer ontevreden ben met de situatie, want deze zogenaamd 'goede theorie' houdt het verwaarlozen van oneindigheden die voorkomen in haar vergelijkingen in, ze verwaarlozen op een willekeurige manier. Dit is gewoon geen zinnige wiskunde. Zinnige wiskunde is het verwaarlozen van een grootheid als ze klein is – niet het verwaarlozen omdat ze oneindig groot is en je haar niet wil!
En andere belangrijke criticus was Feynman. Ondanks zijn cruciale rol in de ontwikkeling van de kwantumelektrodynamica, schreef hij het volgende:[2]
- Dit dopjesspel dat wij spelen ... wordt technisch 'renormalisatie' genoemd. Maar ongeacht hoe intelligent het woord klinkt, ik noem het nog steeds een geschift proces! Dat we naar zulke hocus pocus moeten grijpen, heeft ons belemmerd te bewijzen dat de theorie van kwantumelektrodynamica wiskundig zelfconsistent is. Het is merkwaardig dat de theorie nog steeds niet op de een of andere manier zelfconsistent is bewezen; ik vermoed dat renormalisatie niet wiskundig toegelaten is.
Terwijl Diracs kritiek zich richtte op de procedure van renormalisatie zelf, was die van Feynman verschillend. Feynman was bezorgd dat alle veldentheorieën die in de jaren zestig gekend waren, de eigenschap bezaten dat de interactie oneindig sterk werd bij voldoende hoge energieën. Door deze eigenschap, Landaupool geheten, was het plausibel dat alle theorieën inconsistent waren. In 1974 toonden Gross, Politzer en Wilczek aan dat een andere theorie, kwantumchromodynamica, geen Landaupool heeft. Feynman aanvaardde, samen met de meeste anderen, dat QCD wel een volledig consistente theorie kon zijn.
Het algemene onbehagen was nagenoeg universeel tot de jaren zeventig en tachtig. Vanaf toen, echter, begonnen de meningen te veranderen —dankzij het werk in de renomalisatiegroep en de effectieve veldentheorie, en ondanks het feit dat de oudere generatie, zoals Dirac, hun kritiek nooit terugnamen. Wilson en anderen toonden aan dat de renormalisatiegroep nuttig is in de statistische veldentheorie toegepast op de vastestoffysica, waar deze zorgt voor belangrijke inzichten in het gedrag van faseovergangen. In de vastestoffysica bestaat er een échte regulator voor de kortste afstanden: de materie is niet meer continu op de schaal van de atomen. De divergenties van hoge energieën (of korte afstanden) zorgen in de vastestoffysica niet voor filosofische problemen, aangezien de veldentheorieën daar slechts effectieve voorstellingen zijn van het gedrag van de materie —er zijn geen oneindigheden gezien de cut-off steeds eindig is, en het houdt steek dat de naakte grootheden van deze cut-off afhangen.
Met de kwantumveldentheorieën zou iets gelijkaardigs kunnen gebeuren: in een analoog scenario zouden de natuurwetten anders zijn bij zeer hoge energieën, zodat alle veldentheorieën effectieve benaderingen zijn van de echte natuurwetten. Dit zou dan impliceren dat de divergenties in de kwantumveldentheorieën worden veroorzaakt door de menselijke onwetendheid, en renormalisatie komt dan gewoon neer op het beste maken van de kennis die we hebben. Een gangbare hypothese is, dat er bij de schaal van 1015 GeV iets zou gebeuren, aangezien de koppelingsconstanten van de tegenwoordig bekende theorieën bij die schaal ongeveer gaan samenvallen. Dit zou kunnen leiden tot een eerste stap naar de theorie van alles, waarbij alle natuurkrachten worden samengebald tot één enkele kracht.
Zie ook[bewerken | brontekst bewerken]
Verdere literatuur[bewerken | brontekst bewerken]
Algemene inleiding[bewerken | brontekst bewerken]
- Delamotte, Bertrand (2004). A hint of renormalization. American Journal of Physics 72 (2): 170-184. DOI: 10.1119/1.1624112. Volledige tekst verkrijgbaar op: hep-th/0212049
- Baez, John (2005). Renormalization Made Easy. Een kwalitatieve inleiding.
- Blechman, Andrew E. (2002). Renormalization: Our Greatly Misunderstood Friend. Samenvatting van een lezing met meer informatie over specifieke regularisatie- en subtractieschema's.
- Cao, Tian Yu & Schweber, Silvian S. (1993). The Conceptual Foundations and the Philosophical Aspects of Renormalization Theory. Synthese 97 (1): 33-108. DOI: 10.1007/BF01255832.
- Shirkov, Dmitry (2001). Fifty years of the renormalization group. C.E.R.N. Courrier 41 (7). Volledige text verkrijgbaar op: I.O.P Magazines
Kwantumveldentheorie[bewerken | brontekst bewerken]
- Ryder, Lewis H.; Quantum Field Theory (Cambridge University Press, 1985), [ISBN 0-521-33859-X].
- Zee, Anthony; Quantum Field Theory in a Nutshell, Princeton University Press (2003) [ISBN 0-691-01019-6].
- Weinberg, Steven; The Quantum Theory of Fields (3 delen) Cambridge University Press (1995).
- Pokorski, Stefan; Gauge Field Theories, Cambridge University Press (1987) [ISBN 0-521-47816-2].
- 't Hooft, Gerard; The Glorious Days of Physics – Renormalization of Gauge theories, lezing gegeven te Erice (augustus/september 1998). Volledige tekst verkrijgbaar op: hep-th/9812203.
- Rivasseau, Vincent; An introduction to renormalization, Poincaré Seminar (Paris, Oct. 12, 2002), gepubliceerd in : Duplantier, Bertrand; Rivasseau, Vincent (Eds.) ; Poincaré Seminar 2002, Progress in Mathematical Physics 30, Birkhäuser (2003) [ISBN 3-7643-0579-7].
- Rivasseau, Vincent; From perturbative to constructive renormalization, Princeton University Press (1991) [ISBN 0-691-08530-7].
- Iagolnitzer, Daniel & Magnen, J.; Renormalization group analysis, Encyclopaedia of Mathematics, Kluwer Academic Publisher (1996). Volledig tekst verkrijgbaar in PostScript en pdf hier.
- Scharf, Günter; Finite quantum electrodynamics: The causal approach, Springer Verlag Berlin Heidelberg New York (1995) [ISBN 3-540-60142-2].
Statistische fysica[bewerken | brontekst bewerken]
- Nigel Goldenfeld; Lectures on Phase Transitions and the Renormalization Group, Frontiers in Physics 85, Westview Press (June, 1992) [ISBN 0-201-55409-7]. Vooral inzichtelijk en minder technisch.
- Zinn-Justin, Jean; Quantum Field Theory and Critical Phenomena, Oxford University Press (4th edition – 2002) [ISBN 0-19-850923-5].
- Zinn-Justin, Jean; Phase Transitions & Renormalization Group: from Theory to Numbers, Poincaré Seminar (Paris, Oct. 12, 2002), gepubliceerd in: Duplantier, Bertrand; Rivasseau, Vincent (Eds.); Poincaré Seminar 2002, Progress in Mathematical Physics 30, Birkhäuser (2003) [ISBN 3-7643-0579-7].
- Domb, Cyril; The Critical Point: A Historical Introduction to the Modern Theory of Critical Phenomena, CRC Press (March, 1996) [ISBN 0-7484-0435-X].
- Brown, Laurie M. (Ed.); Renormalization: From Lorentz to Landau (and Beyond), Springer-Verlag (New York-1993) [ISBN 0-387-97933-6].
Allerlei[bewerken | brontekst bewerken]
- Shirkov, Dmitry; The Bogoliubov Renormalization Group, JINR Communication E2-96-15 (1996). Volledig tekst verkrijgbaar op: hep-th/9602024
- Zinn Justin, Jean; Renormalization and renormalization group: From the discovery of UV divergences to the concept of effective field theories, in: de Witt-Morette C., Zuber J.-B. (eds), Proceedings van de NAVO ASI over Quantum Field Theory: Perspective and Prospective, juni 15-26 1998, Les Houches, Frankrijk, Kluwer Academic Publishers, NATO ASI Series C 530, 375-388 (1999). Volledig tekst verkrijgbaar in PDF.
Referenties[bewerken | brontekst bewerken]
- ↑ Kragh, Helge ; Dirac: A scientific biography, CUP 1990, p. 184; originele tekst:
- Most physicists are very satisfied with the situation. They say: 'Quantum electrodynamics is a good theory and we do not have to worry about it any more.' I must say that I am very dissatisfied with the situation, because this so-called 'good theory' does involve neglecting infinities which appear in its equations, neglecting them in an arbitrary way. This is just not sensible mathematics. Sensible mathematics involves neglecting a quantity when it is small – not neglecting it just because it is infinitely great and you do not want it!
- ↑ Feynman, Richard P. ; QED, The Strange Theory of Light and Matter, Penguin 1990, p. 128; originele tekst:
- The shell game that we play ... is technically called 'renormalization'. But no matter how clever the word, it is still what I would call a dippy process! Having to resort to such hocus-pocus has prevented us from proving that the theory of quantum electrodynamics is mathematically self-consistent. It's surprising that the theory still hasn't been proved self-consistent one way or the other by now; I suspect that renormalization is not mathematically legitimate.











