Complex getal
In de wiskunde zijn complexe getallen een uitbreiding van de reële getallen. Zoals de reële getallen overeenkomen met punten op een rechte lijn, correspondeert ieder complex getal met een punt op het complexe vlak. Een complex getal is zodoende een paar reële getallen en , dat gewoonlijk wordt weergegeven als . Hierin is , soms wordt ook gebruikt, een bijzonder complex getal, de imaginaire eenheid, met als eigenschap . Met complexe getallen in de vorm kan gewoon gerekend worden, met de extra rekenregel dat overal vervangen wordt door −1.
De schrijfwijze laat zien dat een complex getal de som is van een reëel getal en een imaginair getal, of anders gezegd, een lineaire combinatie met reële coëfficiënten van 1 en .
De extra mogelijkheden die het rekenen met complexe getallen biedt, hebben geleid tot allerlei nuttige toepassingen in vooral alles wat met trillingen en golven te maken heeft, zoals het grootste deel van de natuurkunde, de elektrotechniek, de meet- en regeltechniek en vele andere technische disciplines.
Uit de definitie van complexe getallen blijkt dat reële getallen ook complexe getallen zijn. Binnen een context waarin nog niet is gespecificeerd of alleen reële of alle complexe getallen worden beschouwd betekent "complex getal" meestal "niet noodzakelijk reëel complex getal". Afhankelijk van de context wordt met een complex getal ook weleens bedoeld een niet-reëel complex getal.
Geschiedenis[bewerken | brontekst bewerken]
De formule van de Italiaanse wiskundigen Scipione del Ferro en Niccolò Tartaglia voor de oplossingen van de derdegraadsvergelijking plaatste de wiskundigen van de zestiende eeuw voor een enorm nieuw probleem. Wanneer zo'n vergelijking drie verschillende (reële) oplossingen heeft, komen in die formule namelijk wortels voor uit negatieve getallen. En in die tijd waren wortels uit negatieve getallen nog niet gedefinieerd. Het is geen wonder dat de naam 'imaginaire getallen' snel gevonden was, en de gewone getallen heetten vanaf toen 'reëel'. Aan het einde van de 18e eeuw legden de grote wiskundigen Leonhard Euler en Carl Friedrich Gauss de basis voor de getallenleer en de functietheorie waarmee dit probleem en vele andere zouden worden opgelost.
De eigenschappen van complexe getallen hebben tot gevolg dat een polynoom van graad in de complexe getallen precies nulpunten heeft, in plaats van ten hoogste nulpunten zoals bij de reële getallen het geval is. Dit is de hoofdstelling van de algebra. Ook geldt dat de vergelijking voor negatieve getallen een oplossing heeft voor alle ongelijk aan 0 in plaats van alleen maar voor oneven waarden van .
Definitie[bewerken | brontekst bewerken]
Complexe getallen voorzien in de behoefte oplossingen te hebben van alle (algebraïsche) vergelijkingen, dus bijvoorbeeld ook vergelijkingen van de vorm voor negatieve getallen .
Eén benadering is het introduceren van een denkbeeldige, imaginaire oplossing, aangeduid met , van imaginair, van de vergelijking . Men stelt dus dat deze vergelijking per definitie een oplossing heeft. Die oplossing wordt genoemd. Door de reële getallen uit te breiden met dit denkbeeldige getal , waarmee verder op de normale manier wordt gerekend, ontstaat de verzameling van de complexe getallen. Deze uitbreiding bevat met vanzelf ook alle uitdrukkingen van de vorm waarin en reële getallen zijn. Hiermee is het gewenste resultaat bereikt: binnen de complexe getallen is elke algebraïsche vergelijking oplosbaar.
De andere benadering is het construeren van de verzameling, waardoor het beeld verdwijnt dat de nieuwe getallen niet echt bestaan. De aanduiding imaginair, overgenomen van de eerste benadering, wordt wel gebruikt, maar hoeft niet letterlijk te worden genomen. Wel is het zo dat klassieke natuurkundige grootheden een reële numerieke waarde hebben. Dit neemt niet weg dat complexe getallen daarbij een handig hulpmiddel kunnen zijn, zie onder.
Definitie door introductie van een nieuw getal i[bewerken | brontekst bewerken]
Een complex getal is een uitdrukking van de vorm , waarin en beide reële getallen zijn en een nieuw getal voorstelt, de imaginaire eenheid, met de eigenschap (rekenregel):
Rafael Bombelli, de bedenker van de imaginaire getallen, stelde de rekenregels op voor complexe getallen. Hierbij stelde hij als axioma de genoemde eigenschap van het complexe getal .
Het getal noemt men het reële deel en het getal het imaginaire deel van het complexe getal , en noteert
De verzameling van de complexe getallen wordt genoteerd als .
De reële getallen vormen een deel van de complexe getallen; het zijn de complexe getallen met imaginair deel gelijk aan 0. Getallen waarvan het reële deel 0 is noemt men zuiver imaginair.
Definitie als koppel reële getallen of als tweedimensionale vector[bewerken | brontekst bewerken]
Een complex getal is een getal dat bestaat uit twee reële getallen. Dit leidt tot een alternatieve definitie, waarin het paar reële getallen zelf als complex getal opgevat wordt en vermeden wordt vooraf de imaginaire eenheid in te voeren.
Dit paar reële getallen kan vervolgens worden opgevat als een vector in een tweedimensionale ruimte, het complexe vlak, waarmee kan worden gerekend zoals met gewone vectoren maar met een extra definitie voor de vermenigvuldiging, zie hieronder, met het karakter van een combinatie van een verschaling en een rotatie. Deze definitie heeft tot gevolg dat het kwadraat van een zuiver imaginair getal een reëel getal oplevert.
De alternatieve definitie luidt:
Een complex getal is een geordend paar van reële getallen, met de gebruikelijke optelling:
en de vermenigvuldiging:
Het getal heet ook hier het reële deel en het getal het imaginaire deel van het complexe getal.
Het koppel wordt genoemd. Het koppel wordt vereenzelvigd met het reële getal . Het koppel is daarmee te schrijven als . Men kan hiermee rekenen met de gebruikelijke rekenregels, aangevuld met de regel . Het is dan niet nodig de genoemde definitie van vermenigvuldiging te onthouden en expliciet toe te passen. Voor is het getal van de vorm ; dit heet een zuiver imaginair getal. Deze getallen vormen de verticale as van het complexe vlak.
Voorstelling[bewerken | brontekst bewerken]

De alternatieve definitie stoelt op de voorstelling van de complexe getallen in het platte vlak. De abstracte definitie roept de vraag op of er ook een concrete voorstelling is van complexe getallen. Omdat de complexe getallen een vectorruimte vormen, voortgebracht door 1 en en een complex getal eenduidig verbonden is met het geordend paar reële getallen als de coördinaten ten opzichte van de basis gevormd door 1 en , ligt het voor de hand om als kandidaat te bezien en op te vatten als het complexe getal . Optellen gaat dus als volgt:
Nu rest nog de vraag of er een geschikte vermenigvuldiging gedefinieerd kan worden voor paren reële getallen, die overeenkomt met de vermenigvuldiging voor complexe getallen. Omdat:
- (zie onder),
zullen we de vermenigvuldiging moeten definiëren als:
Dan geldt:
en
Met de identificatie van (1,0) = 1 en is aan de regels voor complexe getallen voldaan.
De verzameling is, na uitbreiding met de hierboven gedefinieerde vermenigvuldiging, isomorf met de verzameling . Deze constructie levert een meetkundige voorstelling van de complexe getallen op, het complexe vlak genoemd. Deze manier van voorstellen werd in 1806 bedacht door de Zwitserse amateurwiskundige Jean-Robert Argand en wordt wel als arganddiagram aangeduid. De eerste wiskundige, die een meetkundige voorstelling van de complexe getallen gaf, was trouwens Caspar Wessel in 1797, maar zijn werk werd niet opgepakt door anderen, mede omdat hij in het Deens schreef.
Naast de overeenkomsten is een belangrijk verschil tussen en dat de in gebruikte vermenigvuldiging van getallenparen in niet gedefinieerd is.
Met de eerst gegeven definitie zijn de reële getallen vanzelf een deelverzameling van de complexe. Het zijn de complexe getallen met imaginair deel 0.
Met de alternatieve definitie vormen de reële getallen formeel geen deelverzameling van de complexe, maar men kan ze ingebed denken door de reële getallen te identificeren als de complexe getallen van de vorm .
De verzameling van de complexe getallen, met de hierboven gedefinieerde optelling en vermenigvuldiging, is een lichaam.
Voorbeelden[bewerken | brontekst bewerken]
De volgende uitdrukkingen stellen twee complexe getallen voor volgens de eerste definitie: en . We kunnen deze twee complexe getallen optellen:
en ook met elkaar vermenigvuldigen
- ,
waarbij we van de rekenregel gebruikgemaakt hebben om te vervangen door −1.
De volgende uitdrukkingen stellen twee complexe getallen voor volgens de alternatieve definitie: en . We kunnen deze twee complexe getallen optellen:
en ook met elkaar vermenigvuldigen
gebruikmakend van de rekenregels.
Notaties voor complexe getallen[bewerken | brontekst bewerken]
Door de definitie van complexe getallen als elementen van een twee-dimensionale ruimte zijn er een tweetal notaties voor complexe getallen die voor de hand liggen. Deze notaties worden beide gebruikt, vaak naast elkaar.
Cartesische of algebraïsche notatie[bewerken | brontekst bewerken]
Een complex getal kan geschreven worden als . Dit komt overeen met het opvatten van een complex getal als een vector in de tweedimensionale ruimte:
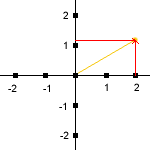
Bij de verticale as worden echter meestal de zuiver imaginaire getallen zelf aangegeven, dus met de .
Dit heet cartesische notatie, naar de wiskundige en filosoof René Descartes, die het cartesisch coördinatenstelsel introduceerde, waarbij een punt in een vlak wordt voorgesteld door een getallenpaar. Daarin is het reële deel en het imaginaire deel van , genoteerd als:
en
In de elektrotechniek wordt meestal het symbool gebruikt voor de imaginaire basisvector, om verwarring met het symbool voor stroom te vermijden.
Notatie met poolcoördinaten[bewerken | brontekst bewerken]
Omdat we de complexe getallen definiëren als elementen van een tweedimensionale ruimte, kunnen we een complex getal ook weergeven in poolcoördinaten, door de afstand van tot de oorsprong en de hoek tussen de vector en het positieve deel van de reële as. Poolcoördinaten kunnen met behulp van de grootte/hoeknotatie worden weergegeven als .
De bovengenoemde afstand wordt de voerstraal, modulus of absolute waarde van het complexe getal genoemd (zie ook onder) en de hoek de poolhoek of het argument van .
Tussen de polaire en cartesische notatie bestaat de betrekking:
of specifieker:
In de andere richting, van cartesisch naar polair, geldt:
Afhankelijk van het resultaat van dient wel gecontroleerd te worden of het resultaat in het juiste kwadrant gelegen is. Om precies te zijn geldt voor het volgende:
 Verband tussen cartesische en poolcoördinaten ter voorstelling van een complex getal. |
Merk op dat argumenten die een veelvoud van 2π verschillen, hetzelfde complexe getal voorstellen. Argumenten van complexe getallen zijn dus niet eenduidig gedefinieerd, op een veelvoud van 2π na. Daarom wordt de hoofdwaarde de waarde van het argument genoemd, die tussen en ligt.
Matrixvoorstelling[bewerken | brontekst bewerken]
Een andere manier om met de complexe getallen te rekenen is door middel van matrices. Het complexe getal wordt daarbij voorgesteld door de 2×2-matrix:
Het getal 1 wordt dus voorgesteld door de eenheidsmatrix:
en de imaginaire eenheid door:
De vermenigvuldiging is de matrixvermenigvuldiging. Inderdaad is:
De complex geconjugeerde van is in de matrixvoorstelling juist de getransponeerde.
In de matrixvoorstelling geldt:
- ,
zodat
Vatten we de matrix op als lineaire transformatie van het -vlak, dan stelt de afbeelding voor die het punt (1,0) afbeeldt op (0,1) en het punt (0,1) op (−1,0). Precies wat we verwachten bij vermenigvuldiging met .
Deze manier van voorstellen is analoog aan de voorstelling van de quaternionen als 2×2-matrices van complexe getallen.
Gerelateerde waarden[bewerken | brontekst bewerken]
Complex geconjugeerde[bewerken | brontekst bewerken]
De complex geconjugeerde of de complex toegevoegde van het complexe getal , met en reëel, is gedefinieerd als:
Uit de definitie volgt onmiddellijk dat
Modulus[bewerken | brontekst bewerken]
De modulus of absolute waarde van een complex getal wordt op dezelfde manier aangegeven als bij reële getallen, dus als , en komt overeen met de euclidische norm in . De berekening ervan gebeurt op de volgende manier:
Anders geformuleerd: de modulus, of absolute waarde, van een complex getal is de lengte van z'n voerstraal. Voor het complexe getal , is de absolute waarde dus:
Uit de definitie van de complex geconjugeerde en de modulus volgt:
Voorbeelden[bewerken | brontekst bewerken]
Modulus van de complex geconjugeerde[bewerken | brontekst bewerken]
Voor de complex geconjugeerde van , geldt:
Ordening[bewerken | brontekst bewerken]
De complexe getallen kunnen niet zoals de reële getallen worden vergeleken door aan te geven welk getal groter is dan het andere, die ordening is er niet. heeft dus geen betekenis.
Rekenen met complexe getallen[bewerken | brontekst bewerken]
Optellen en aftrekken[bewerken | brontekst bewerken]
Het optellen en aftrekken van complexe getallen gaat het makkelijkst in Cartesische vorm: het reële deel en het imaginaire deel worden apart opgeteld. Dit komt overeen met optelling van vectoren.
Twee complexe getallen en worden als volgt opgeteld:
oftewel
Bijvoorbeeld is de som van en :
Uiteraard is aftrekken hetzelfde als het optellen van het tegengestelde.
Merk ook op dat (het nemen van) de complex geconjugeerde distributief is over optellen:
want:
Vermenigvuldigen en delen[bewerken | brontekst bewerken]
Vermenigvuldigen en delen van complexe getallen gaat het makkelijkst in polaire vorm. Hierbij worden de moduli met elkaar vermenigvuldigd en de argumenten bij elkaar opgeteld. Voor getallen in Cartesische vorm geldt voor het product:
oftewel
Dit is feitelijk hetzelfde als het vermenigvuldigen bij de reële getallen, met inachtneming van de definitie .
Verder geldt voor met en met :
en
- ,
dus
Bij het vermenigvuldigen van twee complexe getallen worden de moduli met elkaar vermenigvuldigd en de argumenten bij elkaar opgeteld.
In het bijzonder volgt dat vermenigvuldiging met hetzelfde is als draaiing over radialen, dus een toename van het argument met . Daaruit blijkt weer overeenstemming met de definitie: .
Merk op dat het nemen van het complex geconjugeerde distributief is ten opzichte van het vermenigvuldigen:
omdat:
Merk verder op dat het bovenstaande gegeneraliseerd kan worden:
In het bijzonder:
- voor
- voor
Voor machtsverheffen met moet eerst wat meer gereedschap ontwikkeld worden.
Voor het quotiënt geldt:
Daarbij is gebruikgemaakt van de definitie .
De verzameling vormt met de hierboven beschreven optelling en vermenigvuldiging een lichaam (in België: veld). De eerder geciteerde hoofdstelling van de algebra betekent dat een gesloten lichaam is.
Logaritme en e-macht[bewerken | brontekst bewerken]
De e-macht is een bekende standaardfunctie, die uitgebreid kan worden naar de complexe getallen. Voor een complex getal is de e-macht van gedefinieerd als
Uit deze definitie volgt onmiddellijk
Merk op dat de complexe e-macht zo gedefinieerd is dat deze voor reële waarden van (dat wil zeggen met een imaginair deel 0) overeenkomt met de definitie van de e-macht voor reële getallen.
Door deze definitie behoudt de complexe e-macht een groot aantal "bekende" eigenschappen. Bijvoorbeeld:
Oftewel
Verder volgt uit deze definitie, dat voor alle reële :
en dat
- periodiek is met periode (dus bij constante en variërende )
Uit de eerste van de vijf bovenstaande eigenschappen, , en de polaire notatie volgt nog dat elk complex getal voorgesteld kan worden als:
Met deze vaststelling in de hand, kan ook de natuurlijke logaritme van complexe getallen gedefinieerd worden. Een eigenschap van de natuurlijke logaritme is namelijk dat
Voor een complex getal definieert men op basis van het bovenstaande
- ,
met voor de "normale" definitie van de natuurlijke logaritme voor reële getallen. Aangezien de logaritme zo slechts bepaald is op veelvouden van na, is de afspraak voor altijd de hoofdwaarde te nemen. Daarmee geldt dus dat .
Machtsverheffen[bewerken | brontekst bewerken]
Met de definitie van de e-macht en de logaritme kan ook machtsverheffen voor complexe getallen gedefinieerd worden. En wel is voor de complexe getallen en :
Sinus en cosinus[bewerken | brontekst bewerken]
Met de formule van Euler kan een verband gelegd worden tussen de complexe e-macht en de sinus en cosinus.
en voor :
Zodat uit de som en het verschil van beide relaties volgt dat:
en
Deze twee resultaten hebben drie voordelen:
- door de afleiding zoals hierboven zijn ze zeker intern consistent met de overige rekenregels voor complexe getallen
- deze formules voor de sinus en cosinus komen overeen met de definities voor reëelwaardige argumenten
- door deze identiteiten blijven bewijsbaar de bekende rekenregels voor sinus en cosinus overeind
Merk op dat, overeenkomstig het geval is voor de reële functies, de complexe sinus en cosinus periodieke functies zijn met periode .
Stelling van De Moivre[bewerken | brontekst bewerken]
De eerder uitgewerkte omschrijvingen van goniometrische formules naar e-machten wordt vaak gebruikt om goniometrische functies te reduceren tot meer overzichtelijke polynomen op basis van e-machten en vandaar mogelijk weer tot makkelijkere, goniometrische uitspraken.
Een bekend voorbeeld hiervan is een zeer bekende stelling uit de goniometrie, de stelling van De Moivre. Gegeven het voorgaande is deze stelling overigens triviaal. Volgens deze stelling is:
- Bewijs
Sinus hyperbolicus en cosinus hyperbolicus[bewerken | brontekst bewerken]
Met de complexe e-macht kunnen de definities van de sinus hyperbolicus en de cosinus hyperbolicus uitgebreid worden naar complexe getallen. Voor geldt:
Complexe wortelfuncties[bewerken | brontekst bewerken]
Eerder is vastgesteld dat voor complexe getallen en geldt:
en
Hieruit kan meteen afgeleiden worden wat de -de-machtswortels van een complex getal zijn. Per definitie zijn dit alle oplossingen van de vergelijking .
Het complexe getal dat het meest voor de hand ligt, is waarvoor geldt dat
en
De periodiciteit van de goniometrie leert dat daarnaast ook die complexe getallen een oplossing zijn waarvoor geldt dat:
Dus:
De -de-machtswortels van een complex getal zijn in het complexe vlak dus precies punten, regelmatig verdeeld over een cirkel om de oorsprong, met straal .
Voorbeeld[bewerken | brontekst bewerken]
In het reële domein is de derdemachtswortel uit −1 gelijk aan −1. Maar met bovenstaande rekenregel vinden we dat ook en derdemachtswortels van −1 zijn.
En inderdaad is behalve:
- ,
ook
en
Hoofdwaarde[bewerken | brontekst bewerken]
Zoekt men een unieke oplossing voor de wortelfunctie, dan kan men die waarde kiezen die gebaseerd is op de hoofdwaarde van en daar weer de hoofdwaarde van nemen. In het bijzonder heeft dan de 'unieke' wortel uit −1 de waarde .
Merk op dat de bekende rekenregels niet gelden voor complexe wortels. Zo geldt niet algemeen
Eenheidswortels[bewerken | brontekst bewerken]
Een speciale rol is weggelegd voor de zogenaamde eenheidswortels. Dat zijn de oplossingen van de vergelijking
- ,
waarin een natuurlijk getal is. De oplossingen zijn de punten op de eenheidscirkel (cirkel met straal 1 om de oorsprong) die in polaire notatie gegeven worden door:
Toepassingen[bewerken | brontekst bewerken]
Trillings- en golfverschijnselen[bewerken | brontekst bewerken]
Bovengenoemde eigenschappen en functies van complexe getallen zijn bijzonder nuttig voor het bestuderen van alle periodieke verschijnselen, waaronder golfverschijnselen. In plaats van apart met zowel amplitude als fase te moeten rekenen, kan volstaan worden met één complex getal en de bijbehorende rekentechnieken. Een eenvoudig voorbeeld kan dit aannemelijk maken:
Stel beschrijft een wisselstroom met hoekfrequentie en amplitude . Dit kan worden geschreven als
Deze cosinus is een oplossing van een lineaire differentiaalvergelijking van de tweede orde met constante coëfficiënten.
is ook een oplossing van diezelfde differentiaalvergelijking.
Sinus en cosinus zijn de twee onafhankelijke oplossingen van die differentiaalvergelijking, hetgeen wil zeggen dat de een niet als een veelvoud van de ander is te schrijven. Volgens de theorie van de differentaalvergelijkingen is ook een lineaire combinatie
een oplossing, waarbij en reële constanten zijn. In feite is dit een toepassing van het superpositieprincipe. Dit kan weer herschreven worden als
- , waarbij en (zie arctan2).
In plaats van en zijn nu de amplitude en faseverschuiving de integratieconstanten waarmee de DV aan de randvoorwaarden kan voldoen. Door uitbreiding van met een imaginair deel is een complexe exponentiële functie ontstaan, die de prettige eigenschap heeft dat de afgeleide ervan verkregen wordt door vermenigvuldiging met en de integraal door deling door . De relevante fysische grootheid is .
Hierdoor worden lineaire differentiaalvergelijkingen vereenvoudigd tot algebraïsche uitdrukkingen. Complexe getallen worden ook bij andere soorten differentiaalvergelijkingen gebruikt.
Elektrotechniek en elektronica[bewerken | brontekst bewerken]
Wisselstroom is een periodiek verschijnsel, zodat complexe getallen ook hier het rekenwerk sterk vereenvoudigen, zie ook complexe wisselstroomrekening. Toepassingen liggen bijvoorbeeld in de signaalanalyse, meet- en regeltechniek, analoge en digitale geluids- en beeldbewerking, telecommunicatie, enzovoort. De faseverschuiving, in elektrotechnische spreektaal vaak wat slordig cosinus genoemd, valt met deze complexe rekenwijze eenvoudig te berekenen. Het begrip impedantie kan als complexe grootheid worden beschreven, als complexe impedantie, waardoor de wet van Ohm anders kan worden geschreven:
- complexe spanning = complexe impedantie × complexe stroom.
Hierbij wordt de modulus van de impedantie vermenigvuldigd met de amplitude van de stroom en het argument van de impedantie opgeteld bij de fase van de stroom.
Fourieranalyse wordt veelvuldig gebruikt voor de analyse van tijdafhankelijke signalen, in het bijzonder voor stationaire periodieke signalen. Voor in- en uitschakelverschijnselen, die niet zuiver periodiek zijn, is de laplacetransformatie, een uitbreiding van de fouriertransformatie, onontbeerlijk. Zowel de fourieranalyse als de laplacetransformatie maken deel uit van de functietheorie, voor quasi-stationaire signalen, zoals golfpakketten, zijn er analytische signaalfuncties.
Opmerking: In de elektrotechniek en elektronica wordt de imaginaire eenheid genoemd, om verwarring met de voor de stroomsterkte te voorkomen.
Natuurkunde[bewerken | brontekst bewerken]
Complexe getallen en de bijbehorende complexefunctietheorie worden in de natuurkunde vooral gebruikt om trillingen en golven te beschrijven, zoals in de akoestiek, de wetten van Maxwell, de fysische optica, de fourieranalyse kan in twee dimensies ook op afbeeldingen en buigingspatronen worden toegepast, evenals in de kwantummechanica, waarin golffuncties waarschijnlijkheidsverdelingen beschrijven.
Relativiteit[bewerken | brontekst bewerken]
Een aantal formules voor de ruimtetijd worden in de speciale en de algemene relativiteitstheorie eenvoudiger als men de tijdsvariabele imaginair weergeeft. Dit is niet langer standaard in klassieke relativiteit, maar wordt wel gebruikt in de kwantumveldentheorie. Complexe getallen zijn essentieel voor spinors, die een algemene vorm van de tensoren zijn die in de relativiteitstheorie worden gebruikt.
Meetkunde[bewerken | brontekst bewerken]
Fractals[bewerken | brontekst bewerken]
Bepaalde fractals worden in het complexe vlak weergegeven, bijvoorbeeld de Mandelbrotverzameling en de Juliaverzameling.
Driehoeken[bewerken | brontekst bewerken]
Elke driehoek heeft een unieke Steiners ingeschreven ellips, een ellips binnen de driehoek, die raakt aan het midden van de drie zijden van de driehoek. De brandpunten van driehoekige Steiners ingeschreven ellips kan als volgt worden gevonden, volgens de stelling van Marden:[1][2] Noteer de hoekpunten van de driehoeken in het complexe vlak als, , en . Schrijf de derdegraadsvergelijking , neem daar de afgeleide van en stel deze kwadratische afgeleide gelijk aan nul. De oplossingen van deze vergelijking zijn volgend de stelling van Marden complexe getallen, die de locaties van de twee brandpunten van de Steiners ingeschreven ellips weergeven.
Externe links[bewerken | brontekst bewerken]
- (en) MathWorld. Complex Numbers. overzicht van begrippen
Bronnen, noten en/of referenties
|




















































































































































![{\displaystyle |w|={\sqrt[{n}]{|z|}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f443b78fc34f16cb0302705d330d0508e2653b4)



![{\displaystyle {\sqrt[{n}]{|z|}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03899aeed60a1a9474e6de67d4119e890384ff9a)




























