Gulden snede
| Irrationale getallen: ζ(3) √2 √3 √5 e | |
| Verschillende representaties van de gulden snede | |
| binair | 1,1001 1110 0011 0111 011... |
| decimaal | 1,6180 3398 8749 8948 482...[1] |
| hexadecimaal | 1,9E3779 B97F 4A7C 15F3 9... |
| kettingbreuk | |
| algebraïsch | |

De gulden snede, sectio aurea of sectio divina, ook wel de verdeling in uiterste en middelste reden genaamd, is de verdeling van een lijnstuk in twee delen met een speciale verhouding. Bij de gulden snede verhoudt het grootste van de twee delen zich tot het kleinste, zoals het gehele lijnstuk zich verhoudt tot het grootste. Geven we het grootste deel aan met en het kleinste deel met , dan is de verhouding van beide zo dat .
De bedoelde verhouding wordt het gulden getal genoemd en aangeduid met de Griekse letter (phi); zoals hieronder aangetoond wordt, geldt:
Het getal is dus irrationaal, maar niet transcendent. Er geldt ook:
Hoewel de wiskundige eigenschappen van de gulden snede al in de oudheid werden bestudeerd, dateert de term "gulden snede" pas uit de jaren 30 van de 19e eeuw.
Wiskunde[bewerken | brontekst bewerken]
Euclides[bewerken | brontekst bewerken]
Euclides heeft aangegeven hoe een lijnstuk verdeeld dient te worden om de gulden snede te verkrijgen. Die gulden snede bij het punt S in het lijnstuk AB is zo dat:

- .
Voor de lengten en van de delen betekent dat:
De verhouding heet het gulden getal en wordt aangeduid met .
Daarvoor geldt dus:
- ,
wat leidt tot de vierkantsvergelijking
- ,
- ,
met de positieve oplossing
Opmerking: behalve heeft de vergelijking ook de negatieve oplossing
Constructie met passer en liniaal[bewerken | brontekst bewerken]

De eenvoudigste constructie van de gulden snede gaat als volgt (zie afbeelding):
- Teken een rechthoekige driehoek ABC met de rechthoekszijden AB van lengte 1 en BC van lengte 2. De hypotenusa AC heeft dan de lengte .
- Cirkel vanuit A het punt B om naar het punt D op de hypotenusa.
- Cirkel vanuit C het punt D om naar het punt E op BC. Nu is
- ,
- zodat
- Daaruit volgt:
- ,
- dus:
- Met andere woorden: de zijde BC is verdeeld volgens de gulden snede.
Andere constructie met passer en liniaal[bewerken | brontekst bewerken]

- Construeer een vierkant ABCD met zijden ter lengte 2.
- Bepaal het midden E van AB.
- Cirkel vanuit E het punt C om naar het punt G op het verlengde van AB.
- Dan is B de gulden snede in het lijnstuk AG. Immers:
Gulden rechthoek[bewerken | brontekst bewerken]
Een gulden rechthoek is een rechthoek met zijden in de verhouding van het gulden getal: lengte : breedte = .
Als de breedte is en de lengte , geldt er:
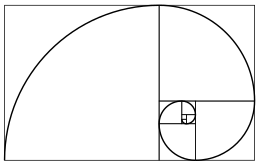
Als we in de gulden rechthoek een vierkant tekenen, met als zijde, is de kleinere rechthoek die overblijft opnieuw een gulden rechthoek. Door dit proces met de steeds kleiner wordende rechthoeken te herhalen ontstaat een gulden spiraal, ook wel fibonacci-spiraal genoemd, naar de rij van Fibonacci.
De gulden rechthoek is langwerpiger dan een rechthoek met de verhouding lengte/breedte gelijk aan de Lichtenberg-ratio (de vierkantswortel uit 2, ongeveer 1,414), waarbij de rechthoek te verdelen is in twee rechthoeken die gelijkvormig zijn aan de hele rechthoek.
Wiskundige benaderingen[bewerken | brontekst bewerken]
De waarde van wordt benaderd door de verhouding van twee opeenvolgende getallen in de rij van Fibonacci. Voor de fibonacci-getallen geldt:
dus
De limiet van dit quotiënt voldoet dus aan:
- ,
dus juist het gulden getal
De machten van kunnen met de fibonacci-getallen worden geschreven.
- , waarin het -de fibonacci-getal is.
Het bewijs hiervan gaat met volledige inductie:
- Inductiebegin voor : , omdat en .
- Inductieveronderstelling, neem aan dat de vergelijking voor een zekere geldig is.
- Inductiestap:
Het gulden getal kan als kettingbreuk geschreven worden door in het rechterlid van de vergelijking , telkens door te vervangen:
en kan als kettingwortel worden uitgedrukt:
Geschiedenis[bewerken | brontekst bewerken]
Wiskunde[bewerken | brontekst bewerken]
Verhandelingen over de gulden snede komen we aanvankelijk alleen op wiskundig gebied tegen. De eerste zou geschreven zijn door Theano, een arts en wiskundige die tot de school van Pythagoras behoorde. Maar dit werk zou verloren zijn geraakt. De eerste die er dan uitdrukkelijk over schreef was Euclides. In zijn Elementen geeft hij de eerst bekende definitie van de gulden snede, die hij aanduidde als extreme en gemiddelde verhouding. Zijn verhandeling over het onderwerp werd in 1509 aan de vergetelheid ontrukt door de Italiaan Luca Pacioli. In De Divina Proportione noemt deze de gulden snede de goddelijke verhouding.
Johannes Kepler beschreef de gulden snede als een kostbaar juweel: "De meetkunde heeft twee grote schatten: de ene is de stelling van Pythagoras, en de andere de verdeling van een lijn in extreme en gemiddelde ratio; de eerste kunnen we vergelijken met een hoeveelheid goud, de tweede mogen we een kostbaar juweel noemen."
Martin Ohm wordt verondersteld de eerste te zijn die de term gulden snede gebruikte om deze verhouding te beschrijven. Hij deed dat omstreeks 1830.
Roger Penrose ontdekte een patroon (de Penrose-betegeling) dat de gulden snede gebruikt in het veld van niet-periodieke vlakvullingen. Dit leidde tot nieuwe inzichten in quasikristallen.
Esthetica[bewerken | brontekst bewerken]
Het duurde tot de 19e eeuw voordat de gulden snede buiten het domein van de wiskunde een bijzondere betekenis werd toegekend.[2] De gulden snede zou sindsdien volgens sommigen een intrinsieke schoonheid bezitten waardoor die verhouding veel zou voorkomen in klassieke architectuur en schilderkunst. De Duitser Adolf Zeising publiceerde in 1854 bijvoorbeeld Neue Lehre von den Proportionen des menschlichen Körpers. In dat boek verdedigt hij de opvatting dat het ideale menselijke lichaam volledig volgens de guldensnedeverhouding is opgebouwd. Ook de beelden die Phidias maakte in het Parthenon worden door sommigen in verband gebracht met de gulden snede. De eerste letter van zijn naam, de Griekse letter , werd daarom door Mark Barr gebruikt om de gulden snede aan te duiden.
De esthetische status van de gulden snede blijft omstreden. Eerder dan ca. 1830 komt de gulden snede niet voor in geschriften over schilderkunst of architectuur en voor de bewering dat de verhouding vaak zou voorkomen of dat de mens een onbewuste voorkeur voor deze verhouding zou hebben, bestaat geen statistisch bewijs. In de loop van de twintigste eeuw verwierf de gulden snede niettemin een plaats in diverse vormen van kunstonderwijs. Terwijl in de schilderkunst de gulden snede grotendeels werd losgelaten - met uitzondering van Salvador Dalí die de gulden snede bewust toepaste - bestaat in de (reclame)fotografie bijvoorbeeld de traditie om significante onderdelen van een foto zodanig in de compositie op te nemen dat er een guldensnede-verdeling ontstaat. Anderen echter beweren dat de gulden snede juist extreem veel wordt toegepast in de Beeldende Kunst en niet alleen door Salvador Dalí. Doordat de gulden snede zo veelvuldig voorkomt in de natuur (zie ook de rij van Fibonacci) zijn we er als mens erg vertrouwd mee. Het is voor onze onderbewuste zintuiglijke verwerking sneller te begrijpen dan wanneer een verhouding niet voldoet aan de gulden snede. Hierdoor is het aannemelijk dat dit universeel als esthetisch wordt ervaren. Dit maakt de verhouding erg geschikt voor allerlei visuele kunsten, van architectuur en product design tot reclame en schilderkunst. De gulden snede maakt het mogelijk een goed gebalanceerd beeld te creëren waarbij de kijker sneller tot de kern komt en zo een betere esthetische ervaring heeft.
Ook in de muziekkunst is de gulden snede aanwijsbaar. Dit geldt met name voor klaviercomposities van Johann Sebastian Bach waarin het expressieve hoogtepunt, qua aantal maten, niet zelden op het snijpunt blijkt te zijn gefixeerd van de basis-getalsverhouding van de gulden snede 1:1,618...
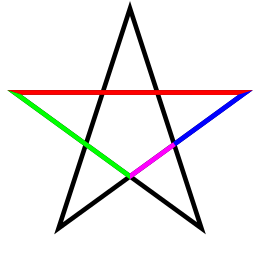
Keltische gnostici gebruikten de gulden snede onder meer in het Noorse pentagram dat ontdekt is door Harald Boehlke.
De Modulor[bewerken | brontekst bewerken]
Een architectonisch maatsysteem dat bewust gebruikmaakt van de gulden snede is de Modulor. Het systeem werd tussen 1942 en 1955 ontwikkeld door de Zwitsers-Franse architect Le Corbusier en bestaat uit twee reeksen van maten: de rode reeks en de blauwe reeks.
Voor de rode reeks nam hij een maat van 183 cm als uitgangspunt—volgens Le Corbusier de lengte van het menselijk lichaam. Door die maat herhaaldelijk door te delen ontstaat de rij 183, 113, 70, 43, 27...
Voor de blauwe reeks deed hij hetzelfde met een maat van 226 cm—de lengte van het menselijk lichaam met uitgestrekte arm. Die maat is tevens een verdubbeling van de 'navelhoogte' (113 cm) die ook al in de rode reeks voorkwam: 226, 140, 86, 54 ...
Een bekend voorbeeld van een op de Modulor gebaseerd gebouw is Le Corbusiers Unité d'Habitation ('wooneenheid'): een "verticale stad" waarvan het eerste exemplaar in 1947 in Marseille werd gebouwd. Later volgden versies in Nantes, Berlijn, Briey en Firminy.
In de natuur[bewerken | brontekst bewerken]

De gulden hoek (ongeveer 137,5°) is de hoek die een cirkel volgens de gulden snede verdeelt. In de natuur zien we die hoek terug in delen van bloemen zoals bloemblaadjes, zaden en kelkbladeren.
Dergelijke bloemdelen groeien uit stukjes weefsel die ontstaan op een vaste plaats, bijvoorbeeld bloemblaadjes die ontspringen in het hart van een bloem. Om optimaal zonlicht te kunnen opvangen is het belangrijk dat de blaadjes allemaal een andere kant op groeien en zo een schijf vormen. Als elk blaadje een gulden hoek met zijn voorganger vormt, wordt de schijf het efficiëntst gevuld.[3] (Vergelijk dit bijvoorbeeld met een zeer inefficiënte hoek: 120°. Het vierde blaadje groeit in dat geval op precies dezelfde plek als het eerste blaadje, het zevende ook, enzovoort. Er ontstaan dan drie pakketjes van over elkaar heen groeiende blaadjes, op 0°, 120° en 240°.)
Een populaire theorie die iets vergelijkbaars beweert over de schelp van de Nautilus pompilius, blijkt bij nameting niet te kloppen. De logaritmische spiraal die door deze schelp wordt gevormd heeft een hoek van 107,04°, een hoek die met de gulden hoek noch met de gulden driehoek in verband valt te brengen.
Zie ook[bewerken | brontekst bewerken]
- Talstelsel met basis gulden snede
- Fractal
- Pisotgetal. Het gulden getal is een pisotgetal.
Bronnen, noten en/of referenties
|









































![{\displaystyle \varphi =1+{\frac {1}{1+{\frac {1}{1+{\frac {1}{1+{\frac {1}{\ldots }}}}}}}}=[1;1,1,1,1,\ldots ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0de2d6a13d3453f75340598e1203ed005b85b04d)
