Stelling van Pythagoras

De stelling van Pythagoras is een wiskundige stelling die het verband geeft tussen de lengten van de zijden van een rechthoekige driehoek:
- In een rechthoekige driehoek is de som van de kwadraten van de lengtes van de rechthoekszijden gelijk aan het kwadraat van de lengte van de schuine zijde.
De stelling is naar de Griekse wiskundige Pythagoras genoemd, maar de stelling was alleen voor de Grieken nieuw. Het resultaat was in Sumer al veel langer bekend en ook in Babylonië en het oude Egypte werd ze al eerder toegepast. In het bijzonder werd de verhouding tussen de beide rechthoekszijden en de schuine zijde al vroeg gebruikt om rechte hoeken uit te meten, zoals dat tot op de dag van vandaag door sommigen nog wordt gedaan. Behalve kennis van de stelling om haar toe te kunnen passen, is ook het leveren van een bewijs belangrijk. Wat dat betreft waren de Grieken, in het bijzonder de pythagoreërs wel de eersten. Zij wisten niet alleen dat de stelling waar was, maar konden ook aantonen waarom zij waar was. In India was de stelling in de zesde eeuw bekend, ze wordt beschreven in vers 17 van de ganitapada uit de Aryabhatiya van Aryabhata, al ontbreekt ook hier het bewijs.[1]
Stelling
De stelling van Pythagoras geeft een verband tussen de lengten van de zijden van een rechthoekige driehoek. Noemt men de lengten van rechthoekszijden, de zijden die aan de hoek van 90° liggen, en , en de lengte van de schuine zijde, de zijde die niet aan de rechte hoek grenst, de hypotenusa, , dan is de bekende wiskundige vorm van de stelling:
Dit is Propositie I.47 uit de Elementen van Euclides.
De stelling van Pythagoras is equivalent met het parallellenpostulaat. Daarom geldt de stelling van Pythagoras niet in niet-euclidische meetkunde.[2]
Voorbeelden
- Uit de stelling van Pythagoras volgt de grondformule van de goniometrie. Voor een rechthoekige driehoek met schuine zijde gelijk aan 1 geldt dat
- Een rechthoekige driehoek heeft rechthoekszijden met lengten en . Volgens de stelling van Pythagoras geldt dan voor de lengte van de schuine zijde:
- Omdat de lengte niet negatief kan zijn, is
- Als de lengten en gegeven zijn, volgt de lengte van de overgebleven zijde uit:
- Waaruit volgt:
Bewijzen
Er bestaan meer dan 350 bewijzen[bron?] voor de stelling van Pythagoras. Onder deze bewijzen zijn er die zijn ontdekt of mogelijk herontdekt door prominenten, zoals James Garfield, de 20e president van de Verenigde Staten, en Multatuli.[bron?]
Bewijs met opdelen vierkant

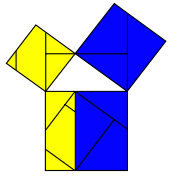
Een van de meer eenvoudige bewijzen deelt een vierkant met zijde op twee manieren in. In de linkerfiguur is het vierkant opgebouwd uit een vierkant met zijde , een vierkant met zijde , en 4 rechthoekige driehoeken. De rechterfiguur is een vierkant opgebouwd uit een vierkant met zijde en dezelfde 4 rechthoekige driehoeken.
Beide figuren tonen een vierkant met zijde , dus beide vierkanten hebben dezelfde oppervlakte. Laat men nu zowel links als rechts de vier rechthoekige driehoeken weg, dan hebben de figuren die overblijven dezelfde oppervlakte. Links blijven een vierkant met zijde en een vierkant met zijde over, met een gezamenlijke oppervlakte van . Rechts resteert een vierkant[3] met zijde . Het vierkant met zijde heeft een oppervlakte van . Hiermee is de stelling bewezen.
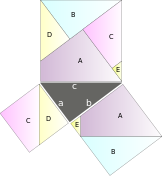
Het kan iets korter: Telkens zijn er een korte en een lange zijde in elkaars verlengde geplaatst. De lengte en breedte van de zijden van het vierkant zijn beide , dus de oppervlakte van het grote vierkant is . De oppervlakte is ook gelijk aan de som van de vier driehoeken plus de oppervlakte van het binnenste vierkant, dat oppervlakte heeft. Dus
Uitwerken van het kwadraat links geeft:
- ,
dus:
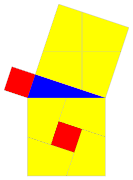
Bewijs met gelijkvormigheid

Een ander inzichtelijk bewijs maakt gebruik van een hulplijn. Hiertoe dient de hoogtelijn vanuit de rechte hoek , die zijde snijdt in het punt .
Het is nu snel in te zien dat driehoek gelijkvormig is aan driehoek . Immers, de hoeken bij zijn dezelfde, en beide driehoeken hebben ook een rechte hoek, bij en bij .
Op dezelfde manier blijkt dat driehoek gelijkvormig is aan driehoek . Er zijn dus drie gelijkvormige driehoeken. Wordt gekeken naar de verhoudingen van de lengtes van de zijden van de driehoeken, dan ziet men dat die gelijk zijn aan , precies de schuine zijden van de drie driehoeken. Dat betekent dat de oppervlaktes van de driehoeken zich verhouden als , de kwadraten van de verhoudingen van de zijden. Omdat , geldt voor een bepaald getal dat . De stelling van Pythagoras volgt door links en rechts door te delen.
Bewijzen zonder woorden
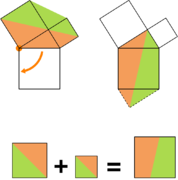
Hoewel geen formeel bewijs, is het bewijs zonder woorden een populaire manier om een stelling te visualiseren zonder daarbij tekst te gebruiken. Van de stelling van Pythagoras zijn dergelijke bewijzen bekend, met name puzzelstukjesbewijzen. Enkele voorbeelden staan hieronder.
-
Animatie
-
Puzzelstukjesbewijs
-
Puzzelstukjesbewijs
-
Animatie
-
Puzzelstukjesbewijs
-
Bewijs bij herschikking
Cosinusregel
Het omgekeerde van de stelling van Pythagoras is ook waar. Als voor een driehoek met zijden en geldt:
dan is die driehoek rechthoekig, met de rechte hoek tegenover de zijde .
Als geldt dat , is de hoek tegenover de zijde scherp. Als , is die hoek stomp. Dit volgt meer precies uit de cosinusregel, die geldt als een uitbreiding van de stelling van Pythagoras voor alle driehoeken.
- ,
waarin de hoek bij hoekpunt is. De stelling van Pythagoras is een bijzonder geval van de cosinusregel, voor het geval .
Pythagorese drietallen
De stelling van Pythagoras geldt voor rechthoekige driehoeken waarvan de rechthoekszijden willekeurige reële getallen zijn, en de Oude Grieken wisten al dat de schuine zijde niet altijd commensurabel is met de rechthoekszijden, zelfs als deze laatsten gehele getallen zijn. Zij hadden echter een bijzondere voorkeur voor meetkundige figuren waarvan de zijden wél onderling commensurabel zijn, d.w.z. dat zij zich verhouden als breuken.
Dit gaf aanleiding tot de zoektocht naar drietallen positieve gehele getallen waarvoor In zekere zin het kleinste drietal dat aan die relatie voldoet, is immers,
Een dergelijk drietal heet pythagorees, en de algemene formule luidt waarbij en willekeurige positieve gehele getallen zijn met
Euclidische afstand

De afstandsformule in het cartesisch coördinatenstelsel is van de stelling van Pythagoras afgeleid. De afstand tussen de punten en in een euclidische ruimte, hun euclidische afstand wordt gegeven door
Wordt gekeken in -dimensionale cartesische coördinaten, dan is de afstand van tot gedefinieerd door
Deze algemene formule kan men afleiden door de afstandsformule in twee dimensies te herhalen. Dit kan men zich voorstellen door in drie dimensies te kijken naar een balk. De ribben in de drie verschillende richtingen horen bij de verschillen van de -, - en -coördinaten. Men vindt nu de lengte van de lichaamsdiagonaal door eerst te zien dat , is recht, en vervolgens dat , ook driehoek is recht. Samen levert dit .
Inwendig-productruimten en niet-euclidische meetkunde
Een inwendig-productruimte heeft de begrippen loodrecht of orthogonaal en lengte of norm in algemenere zin. De stelling van Pythagoras geldt ook hier , zoals in dit voorbeeld van een tweedimensionale functieruimte. Een inwendig-productruimte is een euclidische vectorruimte als deze een eindigdimensionale reële vectorruimte is, maar de stelling van Pythagoras geldt ook als het een oneindigdimensionale vectorruimte is, of een complexe vectorruimte.
De correctheid van de stelling van Pythagoras is in de niet-euclidische meetkunde niet gegarandeerd. Op een boloppervlak is het kwadraat van de schuine zijde van een rechthoekige driehoek in het algemeen strikt kleiner dan de som van de kwadraten van de rechthoekszijden. Een extreem voorbeeld is de gelijkzijdige rechthoekige driehoek gevormd door drie punten die exact 90° van elkaar verwijderd liggen. In de hyperbolische meetkunde geldt dan weer dat de schuine zijde groter is dan wat de formule van Pythagoras zou doen verwachten.
Toepassing
De stelling van Pythagoras vindt toepassing in de volgende voorbeelden:
Websites
- (en) Pythagorean Theorem, met 122 bewijzen[4]
Voetnoten
|