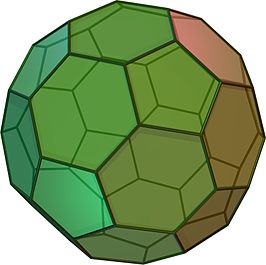
Afgeknotte icosaëder
| Afgeknotte icosaëder | ||||
|---|---|---|---|---|
| ||||
| Vlakken | 12 regelmatige vijfhoeken 20 regelmatige zeshoeken | |||
| Zijden | 32 | |||
| Hoekpunten | 60 | |||
| Ribben | 90 | |||
| Zijvlakken per hoekpunt | 3 | |||
| Ribben per zijvlak | 5 of 6 | |||
| Symmetriegroep | Ih | |||
| Eigenschappen | Halfregelmatig convex | |||
| Duaal veelvlak | Pentakis dodecaëder | |||
| ||||
Een afgeknotte icosaëder is het archimedisch lichaam met hoekpuntconfiguratie 5.6.6. Het heeft 32 vlakken waarvan 20 zeshoekig en 12 vijfhoekig, 60 hoekpunten en 90 ribben. De vijfhoeken grenzen uitsluitend aan zeshoeken, de zeshoeken grenzen om en om aan een vijfhoek en een zeshoek.
Afknotting
Het veelvlak ontstaat als bij een icosaëder de 12 hoeken zodanig worden afgeknot dat van de ribben aan elk van beide kanten 1/3 wordt afgehaald. zodat van de 20 gelijkzijdige driehoeken 20 kleinere regelmatige zeshoeken overblijven, en op de plaats van elk van de 12 hoekpunten een regelmatige vijfhoek ontstaat. Er zijn dan 30 ribben als restanten van de oorspronkelijke 30 langere ribben; ze vormen de helft van de ribben van de 20 zeshoeken, en grenzen elk aan twee ervan. Verder ontstaan er 60 ribben die elk grenzen aan een vijfhoek en een zeshoek.
Symmetrie
De afgeknotte icosaëder heeft net als de icosaëder icosahedrale symmetrie, bij het afknotten blijft alle symmetrie behouden en ontstaat geen extra symmetrie.
Eigenschappen:
- Voor elk paar hoekpunten (P,Q) zijn er twee isometrieën die de afgeknotte icosaëder op zichzelf afbeelden en daarbij P op Q afbeelden.
- Voor elk paar vijfhoekige zijvlakken (R,S) zijn er tien isometrieën die de afgeknotte icosaëder op zichzelf afbeelden en daarbij R op S afbeelden.
- Voor elk paar zeshoekige zijvlakken (R,S) zijn er zes isometrieën die de afgeknotte icosaëder op zichzelf afbeelden en daarbij R op S afbeelden.
- Voor elk paar ribben (T,U) tussen een vijfhoek en een zeshoek zijn er twee isometrieën die de afgeknotte icosaëder op zichzelf afbeelden en daarbij T op U afbeelden.
- Voor elk paar ribben (T,U) tussen twee zeshoeken zijn er vier isometrieën die de afgeknotte icosaëder op zichzelf afbeelden en daarbij T op U afbeelden.
Van de genoemde aantallen isometrieën is steeds de helft een directe isometrie.
Uit het bovenstaande volgt (informeel gezegd) dat alle hoekpuntconfiguraties (ook vertexconfiguratie genoemd) gelijk zijn (en niet alleen lokaal gezien), maar dat er twee soorten zijvlak zijn (binnen elke soort onderling gelijk) en twee soorten ribbe (binnen elke soort onderling gelijk).
Oppervlakte en inhoud
De oppervlakte A en inhoud V van een afgeknotte icosaëder waarbij a de lengte van een ribbe is:
Voorkomen

De vlakverdeling van een afgeknotte icosaëder vindt men veelvuldig terug op het leer of plastic van een voetbal.
Buckminsterfullereen, C60, is een bijzonder koolstofmolecuul dat deze vorm heeft.
Andere polyhedra met vijfhoeken en zeshoeken
Bij alle polyhedra, met een oppervlak topologisch gelijkwaardig met een boloppervlak, en met geen andere zijvlakken dan (niet noodzakelijk regelmatige) vijfhoeken en/of zeshoeken, met steeds drie samenkomend in een hoekpunt, is het aantal vijfhoeken 12. Dit is eenvoudig af te leiden uit de formule van Euler voor veelvlakken.[1]
Zie ook
- ↑ M.C. van Hoorn De formule van Euler voor veelvlakken


