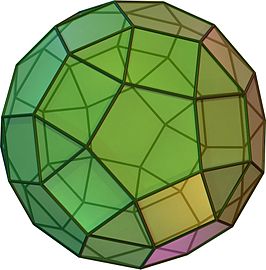
Rombische icosidodecaëder

Romboëdrisch icosidodecaëder
Vlakken	20 driehoeken 30 vierkanten 12 vijfhoeken
Zijden	62
Hoekpunten	60
Ribben	120
Zijvlakken per hoekpunt	4
Ribben per zijvlak	3, 4 of 5
Symmetriegroep	Ih
Eigenschappen	Halfregelmatig convex
Duale vorm	Deltaëdrisch hexacontaëder
Portaal    Wiskunde

Een romboëdrisch icosidodecaëder is een Archimedisch lichaam met 62 vlakken waarvan 20 driehoekig, 30 vierhoekig en 12 vijfhoekig, 60 hoekpunten en 120 ribben.

In elk hoekpunt komen er 1 driehoek, 2 vierkanten en 1 vijfhoek samen.

De oppervlakte A en inhoud V van een romboëdrisch icosidodecaëder waarbij a de lengte van een ribbe is, worden gegeven door:

$A = \left(30+\sqrt{30(10+3\sqrt{5}+\sqrt{15(2+2\sqrt{5})})}\right)~a^2$

$\approx 59,3060~a^2$

$V = {1\over3}(60+29\sqrt{5})~a^3 \approx 41,6153 ~a^3$