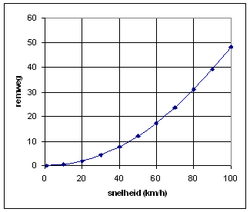
Remweg
De remweg is de afstand die een voertuig aflegt terwijl er wordt geremd. De lengte van de remweg is afhankelijk van de remvertraging en de aanvangssnelheid.
Wiskundig model[bewerken | brontekst bewerken]
Remvertraging[bewerken | brontekst bewerken]
De remvertraging arem wordt bepaald door de verhouding tussen de remkracht Frem en de massa m van het voertuig.
Als een voertuig tweemaal zo zwaar is, bijvoorbeeld vanwege een zware lading, dan neemt bij dezelfde remkracht de remvertraging met de helft af.
Remtijd[bewerken | brontekst bewerken]
De tijd die nodig is om tot stilstand te komen is afhankelijk van de beginsnelheid v0 en de remvertraging.
Remweg[bewerken | brontekst bewerken]
Bij afnemende snelheid wordt de in een tijdspanne t afgelegde weg s in zijn algemeenheid gegeven door:
Wordt dit gecombineerd met de formule om trem te berekenen, dan kan de remweg srem als volgt berekend worden:
In woorden: de lengte van de remweg (in meters) kan worden berekend door het kwadraat van de aanvangssnelheid (in meters per seconde) te delen door tweemaal de remvertraging (in meters per seconde²).
De lengte van de remweg neemt kwadratisch toe met de aanvangssnelheid. Dat houdt in dat als de aanvangssnelheid verdubbelt, de remweg verviervoudigt. Bij een verdrievoudiging van de aanvangssnelheid wordt de remweg negenmaal zo lang. Verder is de remweg omgekeerd evenredig met de remvertraging: een halvering van de remvertraging verdubbelt de lengte van de remweg.
Stopafstand[bewerken | brontekst bewerken]
De remweg is echter niet de hele afstand die nodig is om tot stilstand te komen. Tussen het moment dat de bestuurder van een motorvoertuig een gevaarlijke situatie waarneemt en het moment dat hij of zij daadwerkelijk remt, rijdt het voertuig namelijk nog gewoon door. De afstand die in deze reactietijd tr wordt afgelegd heet de reactieweg. Reactieweg en remweg vormen samen de stopafstand.
Voor bestuurders van motorvoertuigen wordt meestal uitgegaan van een reactietijd van 1 seconde, de zogenaamde "schrikseconde".
Praktijkvoorbeelden[bewerken | brontekst bewerken]


Weggebruikers[bewerken | brontekst bewerken]
De maximale remkracht voor voertuigen op de weg wordt bepaald door de wrijving tussen wieloppervlak en wegdek. Voor personenauto's met goede rubberbanden en een antiblokkeersysteem (ABS) op een schoon, vlak en ruw wegdek ligt de maximale remvertraging tussen 9 en 12 m/s². Voor motorfietsen, fietsen en beladen vrachtwagens is de maximale remvertraging in voorkomende gevallen dezelfde als personenauto's, als zij zijn uitgerust met ABS. Hierin geldt wel dat zij voldoende remkracht moeten kunnen opbrengen (dus in goede goede technische staat zijn en er geen overbelading van het voertuig is). Dan is de remvertraging alleen nog afhankelijk van het toegepaste bandrubber en het wegdek. Is een motorfiets niet uitgerust met ABS dan is er kans dat een remming kan leiden tot een of beide blokkerende wielen. Een blokkerend voorwiel zorgt in dat geval voor te weinig zijdelingse stabiliteit en een val van de motorfiets. Een getrainde motorrijder bereikt op een motorfiets zonder ABS een remvertraging van 8 à 9 m/s², een gemiddelde motorrijder haalt slechts een remvertraging van 6 à 7 m/s². Vrachtwagens beschikken tegenwoordig over een EBS remsysteem. Dit is een elektronisch geregeld remsysteem, dat berekent aan de hand van een paar remmingen of en hoeveel lading er in de aanhangwagen zit en gebruikt dit om de remkrachten van de combinatie af te stemmen. De remkrachten van de truck en aanhanger worden dan zodanig verdeeld dat de combinatie niet gaat scharen of instabiel wordt tijdens een noodremming. Wanneer er geen sprake is van overbelading kan een zwaar beladen vrachtwagen dus met eenzelfde vertraging remmen als personenauto's, mits hun remkracht maar voldoet. Vrachtwagen banden zijn in de regel stugger en slijtvaster dan personenauto banden waardoor ze gemiddeld op schoon en droog asfalt een lagere vertraging halen, rond de 9 m/s². Op een nat, vuil, besneeuwd of slecht wegdek wordt de remvertraging beperkt omdat de maximale wrijving met de ondergrond afneemt.
Treinen[bewerken | brontekst bewerken]
Voor treinen wordt de maximale remvertraging van rond de 1 m/s² deels bepaald door de geringere wrijving tussen metalen oppervlakken (wielen, rails en remblokken) en deels door de hogere massa. Bij eenzelfde aanvangssnelheid is de remweg van een trein ongeveer een factor tien langer dan die van een auto. De remweg van een stoptrein die 90 km/h (25 m/s) rijdt heeft een lengte van ruim 313 meter. Sneltreinen rijden in Nederland met snelheden van 30 tot 35 m/s en hebben een minimale remweg van ruim een halve kilometer. Hogesnelheidstreinen rijden met snelheden in de orde van 60 tot 100 m/s waardoor hun minimale remweg een lengte bereikt in de orde van 2 tot meer dan 5 km.
Schepen[bewerken | brontekst bewerken]
Schepen remmen door de draairichting en de stuwkracht van de schroef om te draaien. Omdat schepen meestal relatief zwaar zijn, remmen schepen over het algemeen erg traag in vergelijking met auto's en treinen. Schepen met een hoge vermogens-gewichtsverhouding, zoals lichte kruisers en sleepboten, hebben de grootste remvertraging. Grote volgeladen tankers uit de ULCC-klasse kunnen op open zee met een snelheid van 16 tot 18 knopen varen (dat is ongeveer 30 tot 33 km/h oftewel 8 à 9 m/s). De lengte van hun remweg kan vanwege hun grote massa oplopen tot enkele tientallen kilometers.
Voorbeeldberekening stopafstand[bewerken | brontekst bewerken]
- Snelheid: 90 kilometer per uur = 25 meter per seconde
- Reactietijd (aanname): 1 seconde
- Reactieweg: 25 meter
- Remvertraging (aanname): 8 meter per seconde²
- Remweg: meter
- Stopafstand: 25 meter + 39 meter = 64 meter
Hellingen[bewerken | brontekst bewerken]

Hellingshoek[bewerken | brontekst bewerken]
Op hellingen wordt de remkracht (en daarmee de remweg) sterk beïnvloed door de hellingshoek (α) en de richting van de helling. Bij onderstaande berekeningen wordt ervan uitgegaan dat het voertuig geen zijwaartse kracht van de helling ondervindt. Verder wordt α positief uitgedrukt als het voertuig de helling oprijdt en negatief als het voertuig de helling afrijdt.
Remkracht en wrijving[bewerken | brontekst bewerken]
De remkracht wordt versterkt of verzwakt door de massa van het voertuig met een bijdrage:
waarin m de massa van het voertuig is, g de valversnelling op Aarde en FG het gewicht van het voertuig. De normaalkracht op de ondergrond wordt verlaagd tot:
waardoor ook de maximale wrijvingskracht met het oppervlak van de helling afneemt tot:
waarin μ een dimensieloze wrijvingscoëfficiënt is.
Remvertraging[bewerken | brontekst bewerken]
De remvertraging langs de helling wordt dan:
Rijdt men de helling af, dan kan de remkracht Frem(α) niet oplopen tot de wrijving op het horizontale vlak maar wordt de remkracht gelimiteerd tot de maximale remkracht . De uitdrukking voor de remweg langs de helling luidt vervolgens:
Voor de maximale remkracht op de helling wordt de uitdrukking voor de remweg:
Kritische hellingshoek[bewerken | brontekst bewerken]
De maximale hoek waarop het voertuig nog net niet vanzelf van de helling naar beneden glijdt, de zogeheten kritische hellingshoek, is afhankelijk van de waarde van de wrijvingscoëfficiënt. De waarde van de wrijvingscoëfficiënt varieert onder normale omstandigheden tussen 0,5 en 0,9.
De kritische hellingshoek is gelijk aan α = arctan μ en ligt onder normale omstandigheden tussen 30° en 40°. Bij gladheid kunnen wrijvingscoëfficiënten en maximale hellingshoeken veel kleiner zijn. De relatieve remweglengten bij maximale wrijving op hellingen met verschillende hoeken worden weergegeven door de waarden van . In onderstaande tabel staan verschillende relatieve remweglengten bij verschillende hellingshoeken en een constante wrijvingscoëfficiënt van (ongeveer 0,58).
| Relatieve stopafstanden | ||
|---|---|---|
| Hellingshoek α (graden) |
||
| 0,0 | 1,0 | 1,0 |
| 5,0 | 0,87 | 1,18 |
| 10,0 | 0,78 | 1,46 |
| 15,0 | 0,71 | 1,93 |
| 20,0 | 0,65 | 2,88 |
| 22,5 | 0,63 | 3,83 |
| 25,0 | 0,61 | 5,74 |
| 27,0 | 0,60 | 9,55 |
| 28,0 | 0,59 | 14,3 |
| 29,0 | 0,58 | 28,7 |
| 29,5 | 0,58 | 57,3 |
| 29,7 | 0,58 | 95,5 |
De tabel laat zien dat de lengte van de remweg voor een helling in opwaartse richting snel naar een minimum convergeert als men de kritische hellingshoek nadert.