Kegelsnede
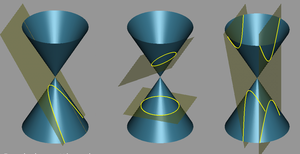
Een kegelsnede is een vlakke lijnvormige figuur die bestaat uit de punten van een kegel (eigenlijk een dubbele kegel) die liggen in een plat vlak dat de kegel snijdt. Kegelsneden werden reeds 200 jaar v.Chr. bestudeerd door Apollonius van Perga. Afhankelijk van de manier waarop de kegel wordt gesneden, is de kegel een enkelvoudige kromme, en wel een cirkel, een ellips of een parabool, of bestaat ze, in het geval van een hyperbool, uit twee krommen. Een cirkel is een speciaal geval van een ellips, zoals een vierkant een speciaal geval is van een rechthoek. Een parabool is op te vatten als een grensgeval tussen een ellips en een hyperbool.
Cirkels, ellipsen en hyperbolen worden wel centrale kegelsneden genoemd omdat ze, in tegenstelling tot een parabool, een middelpunt hebben.
Een kegelsnede wordt vastgelegd door vijf punten waarvan er geen drie op één lijn liggen of door vijf raaklijnen aan een punt op de kegelsnede, waarvan er geen drie door één punt gaan.
Toepassingen[bewerken | brontekst bewerken]
Het tweelichamenprobleem op basis van de omgekeerde kwadratenwet heeft de kegelsneden (bij de hyperbolen: de takken) als oplossingen. Bij het tweelichamenprobleem op basis van gravitatie met de massa van het ene lichaam verwaarloosbaar tem opzichte van de massa van het andere lichaam kan het zware lichaam geacht worden stil te staan, en is de kegelsnede de baan van het lichte lichaam, met het zware lichaam in een brandpunt. Bij een hyperbool is de baan de nabije tak. De specifieke baanenergie is negatief bij een ellips (waaronder een cirkel), namelijk het tegengestelde van de gravitatieconstante maal de massa van het zware lichaam, gedeeld door de lange as. De specifieke baanenergie is nul bij een parabool, en positief bij een hyperbooltak, namelijk de gravitatieconstante maal de massa van het zware lichaam, gedeeld door de afstand van de betreffende hyperbooltak tot de bijbehorende andere hyperbooltak.
Een kogelbaan is bij verwaarlozing van luchtweerstand een kegelsnede die afhangt van het gravitatiemodel. Bij een uniform gravitatieveld is het een parabool. Men spreekt alleen over een kogelbaan als de baan kort is vergeleken met de grootte van de Aarde, en dan is dit een goede benadering. Bij dit model is niet van toepassing dat de specifieke baanenergie nul is bij een parabool. Bovendien is het bij dit model praktisch om de specifieke baanenergie te relateren aan die bij stilstand op een bepaald niveau.

Als wordt uitgegaan van een bolvormige Aarde is de exacte baan een stukje van een ellips, met verticale lange as, en het verre brandpunt in het middelpunt van de Aarde. Bij vergelijking van de specifieke baanenergie in zo'n ellipsbaan met die volgens het andere model moet deze vergeleken worden met die van stilstand op hetzelfde niveau op het aardoppervlak (allebei zijn in dit model flink negatief door de potentiële energie ten opzichte van die op oneindig grote afstand van de Aarde), met eventueel het in beide gevallen buiten beschouwing laten van de draaiing van de Aarde om zijn as.
Bij verwaarlozing van de luchtweerstand resulteert het vanaf de Aarde wegschieten van een kogel in horizontale richting (kanon van Newton) in volgorde van toenemende beginsnelheid in de volgende banen (als de kogel de Aarde raakt uiteraard slechts tot daar):
- ellips met verticale hoofdas en het verre brandpunt in het midden van de Aarde
- cirkel met het middelpunt in het midden van de Aarde
- ellips met verticale hoofdas en het nabije brandpunt in het midden van de Aarde
- parabool met verticale as en het brandpunt in het midden van de Aarde
- hyperbooltak met het nabije brandpunt in het midden van de Aarde
De baan doorloopt zo elk type kegelsnede, en daarvan elke vorm, de ellipsvormen tweemaal. De excentriciteit (zie hieronder) daalt daarbij van 1 naar 0, en stijgt dan van 0 naar oneindig. De excentriciteit stijgt hier namelijk met de beginsnelheid desda de kinetische specifieke beginenergie maal de totale specifieke baanenergie stijgt[1], dit is als de kinetische specifieke beginenergie meer dan -1/2 maal de potentiële specifieke beginenergie is.
Excentriciteit[bewerken | brontekst bewerken]

Vergelijk de ellips, parabool en hyperbool met elkaar. Het verschil tussen deze wordt bepaald door hun excentriciteit.
Ellips[bewerken | brontekst bewerken]
Gegeven zijn twee punten, de brandpunten en , op onderlinge afstand , en een getal , dan is de ellips de meetkundige plaats van de punten waarvoor de som van de afstanden tot de twee brandpunten gelijk is aan .
Parabool[bewerken | brontekst bewerken]
Gegeven zijn een lijn , de richtlijn, en een punt , het brandpunt, niet op de lijn gelegen, dan is de parabool de meetkundige plaats van de punten waarvoor de afstand tot de richtlijn gelijk is aan de afstand tot het brandpunt.
Hyperbool[bewerken | brontekst bewerken]
Gegeven zijn twee punten, de brandpunten en , op onderlinge afstand , en een getal , dan is de hyperbool de meetkundige plaats van de punten waarvoor het verschil van de afstanden tot de twee brandpunten gelijk is aan .
- .
In de ene tak is de afstand tot het ene brandpunt het kleinst, in de andere die tot het andere brandpunt.
Excentriciteit als afstand tot een punt gedeeld door afstand tot een lijn[bewerken | brontekst bewerken]

Het is ook mogelijk een gemeenschappelijke meetkundige definitie te geven voor een punt, een ellips (uitgezonderd de cirkel), een parabool en een hyperbool. Gegeven zijn een lijn de richtlijn, een punt het brandpunt, dat niet op de richtlijn ligt, en een positief getal , de excentriciteit, dan is de meetkundige plaats van de punten die voldoen aan:
een ellips indien , een parabool als (zoals hierboven al behandeld) en een hyperbool als . Als men bij een vast punt en een vaste richtlijn de excentriciteit steeds kleiner maakt, wordt de ellips niet alleen meer cirkelvormig maar ook kleiner. Voor (de excentriciteit van een cirkel) geeft dit slechts het punt . Als men bij een vast punt een ellips steeds cirkelvormiger maakt zonder deze tot een punt samen te trekken, dan beweegt de bijbehorende richtlijn zich naar het oneindige.
Vergelijking[bewerken | brontekst bewerken]
In een cartesiaans assenstelsel is de vergelijking van een kegelsnede van de vorm
met niet alle coëfficiënten gelijk aan nul. Dan nog representeert dit voor sommige combinaties van waarden van de coëfficiënten geen kegelsnede in de genoemde meetkundige zin, zelfs geen ontaarde, want de vergelijking kan ook de lege verzameling representeren (dit geldt bijvoorbeeld voor de vergelijking 1 = 0, maar ook voor en ). Als de vergelijking niet de lege verzameling representeert, representeert deze wel altijd een kegelsnede, eventueel een ontaarde (een punt, een rechte of twee snijdende rechten, zie ook onder).
Het is een kwadratische vergelijking in twee variabelen en . Als
- , is de vergelijking een parabool of een rechte,
- , is de vergelijking een ellips (met als bijzonder geval een punt),
- , is de vergelijking een hyperbool of twee snijdende rechten,
- en , is de vergelijking een cirkel (met als bijzonder geval een punt),
- , is het een rechthoekige hyperbool.
De cirkel heeft daarmee 3 vrijheidsgraden, de parabool 4, en de ellips en de hyperbool 5. Afgezien van de positie en de stand zijn dit er respectievelijk 1, 1, 2 en 2. Afgezien van schaling, dus qua vorm, zijn het er respectievelijk 0, 0, 1 en 1.
Een volledige kegelsnede is (behoudens uitzonderingsgevallen) de grafiek van als functie van in de volgende twee gevallen:
- (parabool met verticale as)
- (hyperbool waarbij een asymptoot verticaal is)
Matrixvergelijking van een kegelsnede[bewerken | brontekst bewerken]
heet de kubische matrix van de kegelsnede bepaald door de vergelijking
Deze vergelijking kan geschreven worden als
met
Raaklijn in een punt van een kegelsnede[bewerken | brontekst bewerken]
De vergelijking van de raaklijn in het punt van de kegelsnede gegeven door de kubische matrix kan geschreven worden als
- Voorbeeld
De raaklijn in het punt van de kegelsnede met vergelijking
wordt gegeven door de vergelijking
Raaklijn vanuit een punt aan een kegelsnede[bewerken | brontekst bewerken]

De verbindingslijn van de raakpunten van de raaklijnen uit een punt aan een kegelsnede met matrixvergelijking heet de raakkoorde corresponderend met punt . Als de raakkoorde bekend is, is het mogelijk de raaklijnen uit aan de kegelsnede te berekenen.
De raakkoorde corresponderend met het punt heeft de vergelijking
Hierin is de kubische matrix van de kegelsnede . Zodra die raakkoorde bekend is, kunnen de snijpunten van en de kegelsnede berekend worden. Die snijpunten en zijn de raakpunten van de raaklijnen uit het punt aan de kegelsnede. De gevraagde raaklijnen zijn dan de lijnen en .
Voorbeeld[bewerken | brontekst bewerken]
We berekenen de raaklijnen uit punt aan de kegelsnede met vergelijking
De raakkoorde corresponderend met het punt heeft als vergelijking
De snijpunten en van die raakkoorde met de kegelsnede zijn de oplossingen van het stelsel
De oplossingen zijn en .
De raaklijn heeft vergelijking .
De raaklijn heeft vergelijking .
Middelpunt van een ellips of hyperbool[bewerken | brontekst bewerken]
Het middelpunt van een ellips of hyperbool is het symmetriepunt van de figuur. De coördinaten van het middelpunt van zo'n kegelsnede met vergelijking zijn de oplossingen van het stelsel
Ontaarde kegelsneden[bewerken | brontekst bewerken]
Behalve deze 'standaard' kegelsneden zijn er ook nog ontaarde kegelsneden. Deze worden gevormd door het snijvlak door de top van de kegel te laten gaan. Dit geeft een punt, een rechte of twee snijdende rechten.
Een kegelsnede is ontaard als zijn vergelijking kan worden ontbonden als een product van twee lineaire vergelijkingen met reële of complexe coëfficiënten. De grafiek valt dan uiteen in twee reële of twee imaginaire rechten. Het zijn de componenten van de ontaarde kegelsnede. Het snijpunt van die rechten heet het dubbelpunt. Wanneer de twee rechten samenvallen is ieder punt een dubbelpunt. Zo is de kegelsnede met vergelijking ontaard in de reële rechten met vergelijking en . Het punt (3,0) is het dubbelpunt. De kegelsnede ontaardt in de imaginaire rechten en en het reële dubbelpunt ligt in de oorsprong (0,0).
Een parabool ontaardt in een rechte en een ellips in twee toegevoegd imaginaire rechten. Een hyperbool ontaardt in twee snijdende reële rechten.
De kegelsnede met vergelijking ontaardt enkel en alleen als
De determinant heet de kubische determinant van de kegelsnede.
Op basis van de definitie van een ellips als meetkundige plaats van de punten waarvoor de som van de afstanden tot twee gegeven punten, de brandpunten, gelijk is aan een gegeven getal, is het uiterste geval dat het gegeven getal de afstand tussen de brandpunten is. Men verkrijgt dan het lijnstuk tussen de brandpunten, en zou dit een ontaarde ellips kunnen noemen. Behoudens het geval van samenvallende brandpunten, waarbij het lijnstuk ontaardt tot een punt, kan een lijnstuk echter niet verkregen worden door een vlak met een kegel te snijden, en zijn er ook geen coëfficiënten waarmee de bovengenoemde vergelijking een lijnstuk representeert.
Een steeds smallere parabool heeft als "limiet" een halfrechte, maar ook deze kan niet verkregen worden door een vlak met een kegel te snijden, en er zijn ook geen coëfficiënten waarmee de bovengenoemde vergelijking een halfrechte representeert. Op basis van de definitie van een parabool als de meetkundige plaats van de punten waarvoor de afstand tot de richtlijn gelijk is aan de afstand tot het brandpunt, is een uiterst geval dat het brandpunt op de lijn ligt. Men verkrijgt dan echter geen halfrechte, maar een hele lijn, net als bij het snijden van een vlak met een kegel, waarbij het vlak evenwijdig is met de zijkant van de kegel, en men het vlak verschuift naar die zijkant: ook hier wordt de parabool steeds smaller, maar bij een breedte nul komt er ineens een halfrechte bij die de lijn completeert.
Poolcoördinaten[bewerken | brontekst bewerken]
In poolcoördinaten ten opzichte van een brandpunt is de vergelijking van een kegelsnede
en voor de verre tak van de hyperbool
waarbij gemeten wordt vanaf de richting waarin de kegelsnede het dichtst bij het brandpunt is, en de semi-latus rectum is (de afstand van het brandpunt naar de kegelsnede in de richtingen loodrecht op de hoofdas).
Zie ook[bewerken | brontekst bewerken]
Bronnen, noten en/of referenties
|















































































