Ellips (wiskunde)


Een ellips (Grieks ἔλλειψις, het tekortschieten) is in de wiskunde een vlakke kromme waarbij de som van de afstanden van alle punten op de kromme tot twee brandpunten constant is. De ellips is een nauwkeurig gedefinieerd speciaal geval van het ruime begrip ovaal.
Een cirkel is een speciaal geval van een ellips, zoals een vierkant een speciaal geval is van een rechthoek.
Een ellips is ook een kegelsnede, gevormd door de snijlijn van een kegel of een cilinder met een plat vlak. Het platte vlak moet hierbij de kegelas respectievelijk de cilinderas snijden. Bij het snijden met de kegel moet de hoek tussen de kegelas en het platte vlak groter zijn dan de helft van de openingshoek van de kegel.
Definitie[bewerken | brontekst bewerken]

Een ellips in de meetkunde is een tweedimensionale figuur die de meetkundige plaats is van alle punten waarvoor de som van de afstanden (rode lijn in de figuur) tot twee gekozen punten, de brandpunten (f1 en f2), een vaste waarde heeft. Een ellips heeft twee assen: het lijnstuk door de brandpunten die tegenovergelegen punten van de ellips verbindt heet de lange as of grote as met halve lengte en het overeenkomstige lijnstuk loodrecht daarop door het midden van de lange as is korte as of kleine as, met halve lengte .
In het geval van een cirkel zijn de lange en korte as even lang en is de richting van de lange as onbepaald. Als de ellips geen cirkel is heeft deze dezelfde symmetrie als een rechthoek. De cirkel heeft meer symmetrie, ook meer dan een vierkant.
Alternatieve definitie uitgaande van brandpunt en richtlijn[bewerken | brontekst bewerken]

Een ellips is de meetkundige plaats van de punten in het plat vlak waarbij de verhouding van de afstand tot een willekeurig punt, brandpunt geheten, tot de afstand tot een willekeurige rechte, richtlijn geheten, constant is. Deze constante verhouding is gelijk aan de excentriciteit van de ellips, voorgesteld door e. Er moet gelden 0<e<1 (zie ook excentriciteit (astronomie)). De excentriciteit bepaalt de vorm van de ellips, aanvullend is er dan parameter a voor de grootte.
Met beide brandpunten van de ellips correspondeert de dichtstbijzijnde richtlijn. Ze zijn evenwijdig aan de korte as, en liggen op een afstand van ervan. De afstand van de ellips tot de richtlijn is , dit is voor ongeveer gelijk aan . De afstand van het betreffende brandpunt tot de ellips is dan ook ongeveer hieraan gelijk. Als van onder naar 1 nadert en gelijk gehouden wordt, en dus naar oneindig nadert, nadert de ellips in de buurt van het betreffende brandpunt en de betreffende richtlijn tot een parabool, met als as de lange as van de ellips, en met een richtlijn die nog steeds loodrecht op die as staat. In hun geheel gezien zijn de zeer lange ellips en de parabool wel zeer verschillend, want de parabool heeft geen korte as en daarmee ook geen tweede as van symmetrie.
Voor een cirkel geldt . Voor een ontaarde cirkel die bestaat uit een punt (de samenvallende brandpunten) is elke lijn richtlijn, voor andere cirkels is er geen richtlijn en is de genoemde definitie/eigenschap niet van toepassing.
Als conflictlijn tussen een cirkel en een punt[bewerken | brontekst bewerken]

De ellips is ook op te vatten als conflictlijn tussen een punt en een cirkel, die dan richtcirkel of directrice wordt genoemd. Het gegeven punt is dan het ene brandpunt, het middelpunt van de gegeven cirkel is het andere brandpunt.
Als contractie van een cirkel[bewerken | brontekst bewerken]
Een ellips ontstaat door een cirkel in één richting met een vaste factor te contraheren, zoals bij orthogonale projectie van een schuin geplaatste cirkel.
Eigenschappen[bewerken | brontekst bewerken]
Excentriciteit[bewerken | brontekst bewerken]
De excentriciteit e van de ellips met halve assen a en b is gedefinieerd als:
Brandpunten[bewerken | brontekst bewerken]
De afstand tussen een brandpunt en het middelpunt is:
Er geldt ook:[1]
Raaklijn[bewerken | brontekst bewerken]
Een raaklijn in een punt aan een ellips is de buitenbissectrice van de hoek brandpunt-raakpunt-brandpunt.
Oppervlakte[bewerken | brontekst bewerken]
De oppervlakte A van een ellips met halve lange as a en halve korte as b wordt gegeven door:
Omtrek[bewerken | brontekst bewerken]

Voor de omtrek van een ellips bestaat geen uitdrukking in elementaire functies. De omtrek kan voorgesteld worden als integraal, die daarom ook elliptische integraal heet. Voor de ellips met als parametervergelijking
- ,
wordt de omtrek gegeven door
Daarin is een elliptische integraal van de tweede soort, hier dalend van voor (lengte van een kwart van de eenheidscirkel) tot voor (lengte van een kwart van de omtrek van een ontaarde ellips die bestaat uit een dubbel doorlopen lijnstuk van lengte 2).
Srinivasa Ramanujan geeft twee goede benaderingen voor de omtrek in §16 van "Modular Equations and Approximations to ";[2] namelijk:
en
waarin
De fouten in deze benaderingen zijn respectievelijk in de orde van en .
Vergelijkingen[bewerken | brontekst bewerken]
Middelpuntsvergelijking[bewerken | brontekst bewerken]
De wiskundige vergelijking voor de ellips met als middelpunt het punt als halve lange (horizontale) as en als halve korte (verticale) as is in het -assenstelsel:
Als het middelpunt van de ellips de oorsprong is, vereenvoudigt zich dit tot:
(Voor de afleiding uit de eerder vermelde definitie van een ellips, zie onder.)
In poolcoördinaten t.o.v. middelpunt[bewerken | brontekst bewerken]
In poolcoördinaten t.o.v. een brandpunt[bewerken | brontekst bewerken]
Lange as horizontaal, linker brandpunt als pool, met excentriciteit
In iets algemenere vorm van een ellips met één brandpunt als pool en de andere in een hoek ten opzichte van de oorsprong:
(Zie ook de poolvergelijking van een kegelsnede.)
Parametervergelijking[bewerken | brontekst bewerken]
De parametervergelijking voor de ellips met als middelpunt het punt als halve lange (horizontale) as en als halve korte (verticale) as luidt:
Constructie van een ellips[bewerken | brontekst bewerken]
Tuinmansellips[bewerken | brontekst bewerken]


Een ellips kan als volgt worden getekend:
- Druk twee punaises in de brandpunten, of sla twee spijkers in een plank.
- Maak een lus van een draadje en leg die lus rond de punaises.
- Zet een potlood tegen het draadje aan en trek het strak.
- Teken met het potlood de ellips. Zorg er daarbij voor dat het draadje strak blijft.
Het draadje zorgt ervoor dat de som van de afstand tot de brandpunten vanaf elk punt van de ellips constant is, namelijk gelijk aan de lengte van het draadje minus de afstand tussen de punaises.
Het op deze wijze construeren van een ellips wordt ook wel tuinmansellips genoemd, omdat zo de randen van ellipsvormige perken worden aangelegd, uiteraard met piketten in plaats van punaises. Deze methode is in de praktijk onnauwkeurig. Varianten op de tuinmansmethode kunnen gebruikt worden om diverse ovalen te construeren.
Indien de gewenste afmetingen van het perk zijn, lange as bij korte as, waarbij wordt verondersteld, leidt dit tot de volgende afstand tussen de piketten:

De lengte van de draad – de lus – rond de piketten is dus gelijk aan .
Ellipspasser[bewerken | brontekst bewerken]
De Nederlandse wiskundige Frans van Schooten bedacht in de 17e eeuw twee typen ellipspassers. De gebruikelijkste is een kruisvormige, de andere hanteert een variant van de tuinmansmethode. Van de bekende ellipsconstructies die met eenvoudige mechanische middelen te maken zijn, is de kruisvormige passer in de praktijk de nauwkeurigste.
Constructie van Graves[bewerken | brontekst bewerken]
Bij een gegeven ellips kan met een lus van draad, langer dan de omtrek van de gegeven ellips, een nieuwe ellips geconstrueerd worden: span met een potlood de lus strak om de ellips en teken zo rondgaand de nieuwe figuur. Er ontstaat een tweede ellips met dezelfde brandpunten als de gegeven ellips. Dit is de constructie van Graves.
Constructie uitgaande van de parametervergelijking[bewerken | brontekst bewerken]

Een andere manier om een ellips te tekenen gaat uit van de ingeschreven en omgeschreven cirkel en de parametervergelijking. De straal (radius) van de omgeschreven cirkel is gelijk aan de halve lange as van de ellips, en die van de ingeschreven cirkel is gelijk aan de halve korte as van de ellips. Deze cirkels zijn concentrisch; zij hebben hetzelfde middelpunt. Trek nu vanuit het middelpunt van de cirkels een gemeenschappelijke straal naar buiten toe (zie animatie, in het rood). Vanuit het punt waar die straal de ingeschreven cirkel snijdt, trek je een lijn naar buiten toe (fig.: goud) en evenwijdig met de lange as van de te bekomen ellips, en waar de straal de omgeschreven cirkel snijdt, trek je een lijn naar binnen toe en evenwijdig met de korte as van de te bekomen ellips. Waar beide lijnen elkaar snijden, bevindt zich een nieuw punt van de ellips (fig.: groen).
Afleiding van de vergelijking[bewerken | brontekst bewerken]

De nevenstaande figuur laat een ellips zien met middelpunt in de oorsprong en de lange as langs de x-as. De halve lange as is en de halve korte as Een punt op de ellips heeft de afstanden en tot de respectievelijke brandpunten en , die op een afstand van het middelpunt liggen.
Voor op de positieve y-as geldt volgens de stelling van Pythagoras:
waaruit de formule voor de afstand van brandpunt tot middelpunt volgt:
Voor de afstanden en geldt volgens Pythagoras:
en
zodat:
Nu is
volgens de definitie van een ellips geldt voor de som:
zodat voor het verschil geldt:
Oplossen levert:
- en
Daaruit volgt weer:
Anderzijds geldt:
zodat:
of anders geschreven:
Omdat volgt:
Uit deze berekeningen volgt dat voor een punt op de ellips de coördinaten voldoen aan de vergelijking
Omgekeerd kan men aantonen dat als voor een willekeurig punt de coördinaten voldoen aan die vergelijking, het punt noodzakelijk op die ellips ligt.
Conclusie: de vergelijking van die ellips is
Bollen van Dandelin[bewerken | brontekst bewerken]
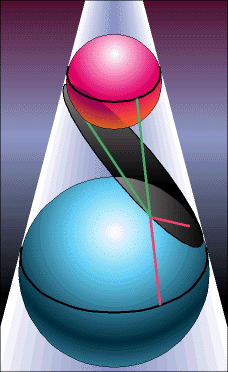
Dat deze meetkundige plaats inderdaad een kegelsnede is, kan worden ingezien met de bollen van Dandelin, genoemd naar Germinal Pierre Dandelin, waar gebruik wordt gemaakt van het feit dat alle raaklijnen vanuit een punt aan een bol even lang zijn. De bollen die in de kegel zijn geplaatst, raken de ellips in de brandpunten (zie figuur).
Zie ook[bewerken | brontekst bewerken]
- Ellipsoïde (omwentelingslichaam van een ellips)
- Kegelsnede
- Superellips
- Slakstructuur (Architectuur/Stedenbouw)
- Pseudo-ellips
- Eerste wet van Kepler: een planeet beschrijft een ellipsbaan rond de zon
- Ovaal
Externe link[bewerken | brontekst bewerken]
Bronnen, noten en/of referenties
|


































































