Fresnelvergelijkingen

De fresnelvergelijkingen of wetten van Fresnel, ontdekt door Augustin Jean Fresnel, beschrijven hoe licht breekt en weerkaatst als het op een grensvlak tussen stoffen met een verschillende brekingsindex valt.
Definities[bewerken | brontekst bewerken]
Als licht een grensvlak ontmoet tussen stoffen met een verschillende brekingsindex (n1 en n2) kan zowel weerkaatsing als breking optreden.
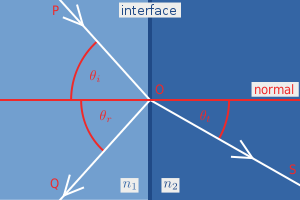
In de bijgaande figuur treft een invallende lichtstraal PO in O het grensvlak tussen twee media (stoffen) met brekingsindex n1 en n2. Een deel van de straal wordt weerkaatst als de straal OQ en een ander deel gebroken als de straal OS. De hoeken die de invallende (i = invallend), weerkaatste (r = reflectie) en gebroken (t = transmissie) bundels maken met de normaal op het grensvlak worden aangeduid met respectievelijk θi, θr en θt. Het verband tussen die hoeken is de reflectiewet en de wet van Snellius.
Formules voor weerkaatsing en breking[bewerken | brontekst bewerken]
De invallende energie Ii (of energie per tijd, oftewel vermogen) wordt verdeeld over de weerkaatste en gebroken bundels. De fracties van de energie in de weerkaatste en gebroken bundels worden aangeduid als respectievelijk de reflectiecoëfficiënt R en de transmissiecoëfficiënt T.[1] We veronderstellen dat de stoffen niet-magnetisch zijn. Dus:
- en
Vanwege behoud van energie geldt
- .
De waarden van R en T hangen af van de polarisatie van de invallende lichtstraal. Als het licht gepolariseerd is met de vector van het elektrisch veld haaks op het vlak van de bijgaande figuur (s-gepolariseerd), dan geldt voor de reflectiecoëfficiënt:
waarin θt berekend kan worden uit θi met de wet van Snellius. De formule is vereenvoudigd met behulp van formules uit de goniometrie.
Voor invallend licht dat in het vlak van de bijgaande figuur gepolariseerd is (elektrische vector in het vlak van de figuur, p-polarisatie), geldt:
De bijbehorende transmissiecoëfficiënten T worden gegeven door en .[2]
Voor ongepolariseerd invallend licht (een gelijk mengsel van s- en p-polarisaties), is de reflectiecoëfficiënt .
Soortgelijke vergelijkingen gelden voor de verhoudingen van de coëfficiënten voor de elektrische veld-amplitudes: deze heten ook fresnelvergelijkingen.
Brewsterhoek[bewerken | brontekst bewerken]
Voor een bepaalde hoek is bij gegeven brekingsindices n1 en n2 Rp gelijk aan nul en wordt een p-polariseerde invallende lichtstraal dus geheel gebroken zonder weerkaatsing. Deze hoek staat bekend als de Brewsterhoek en ligt rond de 56° voor breking van glas naar lucht en rond 53° voor breking van water naar lucht. Dit geldt alleen als de brekingsindices van beide stoffen reële getallen zijn.Voor stoffen die licht absorberen, zoals metalen en halfgeleiders is n een complex getal en wordt Rp in het algemeen voor geen enkele invalshoek gelijk aan nul.
Grenshoek[bewerken | brontekst bewerken]
Als een lichtstraal van een dichter naar een ijler medium loopt (dat wil zeggen n1 > n2), dan wordt boven een bepaalde kritieke hoek, de grenshoek, alle licht weerkaatst en wordt Rs = Rp = 1. Dit verschijnsel heet totale (interne) weerkaatsing. De grenshoek voor glas in lucht ligt bij 41.8°.

Loodrechte inval[bewerken | brontekst bewerken]
Als het licht vrijwel loodrecht invalt op het grensvlak (θi ≈ θt ≈ 0) worden de reflectie- en transmissiecoëfficiënten gegeven door:
Glas[bewerken | brontekst bewerken]
Voor standaard glas is de reflectiecoëfficiënt ongeveer 0,04. De weerkaatsing van een ruit gebeurt zowel aan de voor- als achterkant, waarbij een deel van het licht heen en weer weerkaatst wordt tussen beide kanten. De gecombineerde reflectiecoëfficiënt hiervoor is 2R/(1 + R), als interferentie verwaarloosd kan worden.
Interferentie[bewerken | brontekst bewerken]
Er treedt interferentie op bij meervoudige weerkaatsing van licht tussen twee evenwijdige grensvlakken: teruggekaatste en doorgelaten lichtstralen versterken en verzwakken elkaar, zoals bijvoorbeeld in olie die op water drijft. Dit effect wordt toegepast in Fabry-Pérot-interferometers, anti-reflectiecoatings en andere optische filters.
Algemene formules[bewerken | brontekst bewerken]
In dit artikel wordt verondersteld dat de permeabiliteit μ in beide stoffen gelijk is aan die voor vacuüm, μ0 . Bij benadering is dit juist voor de meeste diëlektrische materialen. De algemene fresnelvergelijkingen zijn ingewikkelder.
Zie ook[bewerken | brontekst bewerken]
Externe links[bewerken | brontekst bewerken]
- (en) Fresnel Equations – Wolfram
- (en) FreeSnell – Gratis software berekent de optische eigenschappen van multilayers.
- (en) Thinfilm – Webformulier om de optische eigenschappen van dunne lagen (thin films) en multilayers te berekenen. (Reflectie- en transmissiecoëfficiënten, ellipsometrische parameters psi en delta)
- (en) Webformulier om de hoeken en intensiteiten bij weerkaatsing en breking te berekenen voor een eenvoudig enkel grensvlak.
- (en) ReflectionCoefficient.INFO – Berekening van de reflectiecoëfficiënt
Bronnen, noten en/of referenties
|




![{\displaystyle R_{s}=\left[{\frac {\sin(\theta _{t}-\theta _{i})}{\sin(\theta _{t}+\theta _{i})}}\right]^{2}=\left[{\frac {n_{1}\cos(\theta _{i})-n_{2}\cos(\theta _{t})}{n_{1}\cos(\theta _{i})+n_{2}\cos(\theta _{t})}}\right]^{2}=\left[{\frac {n_{1}\cos(\theta _{i})-n_{2}{\sqrt {1-\left({\frac {n_{1}}{n_{2}}}\sin \theta _{i}\right)^{2}}}}{n_{1}\cos(\theta _{i})+n_{2}{\sqrt {1-\left({\frac {n_{1}}{n_{2}}}\sin \theta _{i}\right)^{2}}}}}\right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ca9921332e1a67695390bdeacbb81f8d1b7d5d0)
![{\displaystyle R_{p}=\left[{\frac {\tan(\theta _{t}-\theta _{i})}{\tan(\theta _{t}+\theta _{i})}}\right]^{2}=\left[{\frac {n_{1}\cos(\theta _{t})-n_{2}\cos(\theta _{i})}{n_{1}\cos(\theta _{t})+n_{2}\cos(\theta _{i})}}\right]^{2}=\left[{\frac {n_{1}{\sqrt {1-\left({\frac {n_{1}}{n_{2}}}\sin \theta _{i}\right)^{2}}}-n_{2}\cos(\theta _{i})}{n_{1}{\sqrt {1-\left({\frac {n_{1}}{n_{2}}}\sin \theta _{i}\right)^{2}}}+n_{2}\cos(\theta _{i})}}\right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a89a7077a94420e1c29d1ab05013b63414ec9bf9)




