Elektrische weerstand (eigenschap)
| Elektromagnetisme | |
|---|---|
 | |
| elektriciteit · magnetisme | |
Elektrische weerstand of resistantie is de elektrische eigenschap van materialen om de doorgang van elektrische stroom te belemmeren. Vloeit door een materiaal een elektrische stroom, dan gebeurt dit niet ongehinderd, er is energie voor nodig: de stroom ondervindt een zekere weerstand. Deze elektrische energie wordt omgezet in warmte. In formules wordt voor de weerstand de letter R gebruikt, afgeleid van het latijnse resistere.
Weerstand wordt uitgedrukt in de SI-eenheid ohm, met als eenheidssymbool de hoofdletter omega (Ω).
Een elektronische component die wordt ingezet voor zijn elektrische weerstand, heet eveneens weerstand.
Het begrip weerstand[bewerken | brontekst bewerken]
Weerstand is het omgekeerde van geleidingsvermogen. Materialen waarin elektrische ladingen zich kunnen verplaatsen, hebben een zeker geleidingsvermogen en daarmee een zekere weerstand. Is het geleidingsvermogen groot en dus de weerstand klein, zoals bij de meeste metalen, dan spreken we van een geleider. Is geen geleiding mogelijk, dan noemen we het materiaal een isolator. Ook materialen met een zeer hoge weerstand worden als isolator aangeduid. Een bijzondere tussenpositie nemen de halfgeleiders in.
Ook het menselijk lichaam en lucht hebben een eindige weerstand.
Sommige materialen vertonen het verschijnsel van supergeleiding. Beneden een bepaalde, veelal extreem lage, temperatuur verdwijnt hun weerstand volledig.
Wet van Ohm[bewerken | brontekst bewerken]
De relatie tussen de spanning over, de stroom door en de weerstand van een object wordt gegeven door de wet van Ohm:
waarin U de elektrische spanning is over het object uitgedrukt in volt, I de elektrische stroom is door het object uitgedrukt in ampère en R de weerstand uitgedrukt in ohm.
Geleidbaarheid[bewerken | brontekst bewerken]
Het omgekeerde van weerstand is geleidbaarheid (G):
De eenheid voor geleidbaarheid is de siemens (S).
Soortelijke weerstand (Wet van Pouillet)[bewerken | brontekst bewerken]
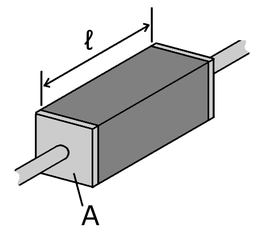
De weerstand van een component kan berekend worden uit zijn fysische eigenschappen. De weerstand(swaarde) van een homogene staaf (of draad) is evenredig met zijn lengte en de soortelijke weerstand (of weerstandscoëfficiënt) van het materiaal en omgekeerd evenredig met de oppervlakte van de dwarsdoorsnede van de staaf:
Daarin is de weerstand in ohm, de soortelijke weerstand in ohm·meter, de lengte in meter en de oppervlakte in vierkante meter van de dwarsdoorsnede. Voor een draad met cirkelvormige doorsnede met diameter is .
De soortelijke weerstand is een kenmerkende materiaaleigenschap die echter ook van bijvoorbeeld de temperatuur afhangt. Soortelijke weerstanden worden meestal — al dan niet afhankelijk van de temperatuur — gemeten met de Van der Pauw-methode.
Ohms materiaal[bewerken | brontekst bewerken]
Ohms materiaal is een materiaal waarvoor geldt dat de spanning en de stroomsterkte een lineaire relatie hebben, dat wil zeggen dat de weerstand constant is over een groot bereik. Een ideale weerstand heeft een constante weerstand bij elke frequentie en is onafhankelijk van de aangelegde spanning of stroom door die weerstand.
Niet alle materialen gedragen zich als ohms materiaal. Hiervan wordt gebruikgemaakt in bijvoorbeeld spanningsafhankelijke weerstanden, waarvan de waarde in sterke mate afhankelijk is van de elektrische spanning die erover staat, ook VDR of varistor genoemd.
Weerstandsvariaties[bewerken | brontekst bewerken]
Onder invloed van omgevingsfactoren kan de weerstand van bepaalde materialen veranderen. Enkele voorbeelden zijn:
- temperatuur
- druk of rek. De werking van rekstrookjes is gebaseerd op dit gegeven.
- luchtvochtigheid
- licht
- spanning
Voor alle bovengenoemde factoren bestaan speciale componenten die als sensor voor een meetinstrument kunnen worden gebruikt.
Men spreekt van weerstanden met een positieve of negatieve temperatuurscoëfficiënt (PTC-weerstand of NTC-weerstand), al naargelang de weerstand toe- of afneemt met de temperatuur. Een thermistor is een voorbeeld van een NTC-weerstand.
Een weerstand ontleent zijn eigenschap aan een weerstandsmateriaal, waarvoor koolstof en legeringen van metaal gebruikt worden. De meeste weerstanden zijn op koolstof gebaseerd. Een massaweerstand bestaat volledig uit koolstof. Andere typen zijn uitgevoerd met een koolstoflaagje, al dan niet gespiraliseerd. Weerstanden met weerstandsdraad van een geschikte metaallegering worden gewikkeld om een kern, teneinde voldoende lengte van de draad in een klein volume te kunnen verwerken. Gewikkelde weerstanden hebben het nadeel dat bij hogere frequenties de zelfinductie van de wikkeling niet te verwaarlozen is, tenzij ze bifilair gewikkeld worden. Naast precisieweerstanden van weerstandsdraad zijn er ook weerstanden met een metaalfilm.
Weerstand en impedantie[bewerken | brontekst bewerken]
Naast de weerstand als typische materiaaleigenschap wordt ook weerstand aan elektrische wisselstroom geboden door spoelen en condensatoren. De verhouding van de (complexe) spanning en de (complexe) stroomsterkte wordt gegeven door de complexe impedantie:
- ,
waarin de weerstand is en de zogeheten reactantie. De weerstand leidt tot vermogensverlies en de reactantie tot faseverschuiving tussen de spanning en de stroom.
Voor de absolute waarden van de spanning, van de stroomsterkte en van de impedantie geldt weer de wet van Ohm:
Codering van weerstanden[bewerken | brontekst bewerken]
Omdat een component in een elektronische schakeling vaak te klein is om cijfers op te drukken, wordt voor het aangeven van de waarde veelal een kleurcode gebruikt.
Worden er toch letters en cijfers gebruikt, dan wordt gewoonlijk het teken Ω weggelaten en schrijft men het voorvoegsel (een hoofdletter E, K of M) in plaats van de komma. Bijvoorbeeld 4K7, waarmee 4,7 kΩ wordt bedoeld, of 82E, wat 82 Ω betekent. Dezelfde codering wordt ook gebruikt bij de tekst in schakelschema's en dergelijke.
Hoeveel procent de weerstand mag afwijken, ziet men aan de laatste ring: die heeft een gouden (5%) of zilveren (10%) kleur.
Vervangingsweerstand of substitutieweerstand[bewerken | brontekst bewerken]
In een elektrisch systeem hebben alle componenten een zekere weerstand. Het uitrekenen van de substitutieweerstand over een systeem gaat, als het gaat om ohmse weerstanden, op een welbepaalde manier.
Serieschakeling[bewerken | brontekst bewerken]
Omdat de spanningen over de losse weerstanden worden opgeteld bij een gelijkblijvende stroom, vindt men met de wet van Ohm
met
- de vervangingsweerstand
- weerstand 1
- weerstand 2, enz.
De substitutieweerstand of vervangingsweerstand is dus groter dan de grootste weerstand in de serieschakeling
Parallelschakeling[bewerken | brontekst bewerken]
Hier staan de weerstanden naast elkaar in de schakeling, zodat de spanning over alle weerstanden dezelfde is, terwijl de stroom zich verdeelt over de takken. Uit de wet van Ohm volgt
met
- de vervangingsweerstand
- weerstand 1
- weerstand 2, enz.
Voor twee parallel geschakelde weerstandenwordt dit: .
De vervangingsweerstand in een parallelschakeling is kleiner dan elk van de samenstellende weerstanden, omdat de doorgang voor de stroom makkelijker wordt door vertakkingen.
Voorbeeld: De vervangingsweerstand van een parallelschakeling van een weerstand van 10 kΩ en een van 20 kΩ is: kΩ
Inwendige weerstand[bewerken | brontekst bewerken]
De term inwendige weerstand of interne weerstand wordt gebruikt bij een component in een stroomkring die niet bedoeld is als weerstand, maar als bijkomend effect wel een weerstand heeft. Dit is bijvoorbeeld van toepassing bij een spanningsbron of spoel.

























