Lorentzkracht

Elektromagnetisme

Elektriciteit · Magnetisme Elektrostatica Elektrische lading · Elektrisch veld Elektrische potentiaal · Wet van Coulomb Elektrische flux · Wet van Gauss Magnetostatica Magnetisch veld · Elektrische stroom Wet van Ampère · Lorentzkracht Magnetische flux · Dipoolmoment Elektrodynamica Inductie · Wetten van Maxwell Elektromagnetische golf Wet van Faraday Elektriciteitsleer Spanning · Stroom · Weerstand Condensator · Spoel · Impedantie Wet van Ohm Wetenschappers Ampère · Coulomb · Faraday · Gauss Lorentz · Maxwell · Ohm · Tesla Volta · Weber · Ørsted

De lorentzkracht is bekend als de kracht van een magnetisch veld op een bewegende lading. De natuurkunde hanteert een algemenere definitie die ook rekening houdt met het elektrisch veld: "De lorentzkracht is de kracht die op een lading wordt uitgeoefend door een elektromagnetisch veld". De elektrische kracht kan een geladen deeltje versnellen of vertragen. De magnetische kracht kan alleen de baan van het deeltje afbuigen.

De lorentzkracht is vernoemd naar de Nederlandse natuurkundige Hendrik Lorentz. Vooral de magnetische kracht is bijzonder omdat de grootte afhangt van de snelheid van het deeltje en omdat de richting loodrecht staat op die van het magnetisch veld. Het bestaan kan worden verklaard met behulp van relativistisch elektromagnetisme. Omdat elektrische stroom veroorzaakt wordt door bewegende lading, werkt de lorentzkracht ook op geleiders in (elektro)magnetische velden.

Formulering

Een deeltje met elektrische lading q komt van links met snelheid v. Een magneetveld B is naar ons toe gericht (pijlpunt in cirkel).

Stel dat een deeltje beweegt door een elektrisch- en een magnetisch veld (of door één van beide). Het deeltje ondervindt dan een elektrische kracht (eenheid: Newton):

$\vec{F}_{e} = q\vec E$

en een magnetische kracht (eenheid: Newton):

$\vec{F}_{b} = q\vec v \times \vec B$

Daarbij is E het elektrisch veld (in volt per meter), B het magnetisch veld (in Tesla), q de elektrische lading (in Coulomb) en v de snelheid van het deeltje (in meters per seconde).

Samen vormen ze de lorentzkracht (eenheid: Newton):

$\vec F_L = \vec{F}_{e} + \vec{F}_{b} = q (\vec E + \vec v \times \vec B)$

De elektrische kracht werkt in de richting van het elektrisch veld, en geeft dus een versnelling ongeacht de bewegingsrichting van het deeltje. Het uitwendig product ($\mathbf{\times}$) geeft aan dat de magnetische kracht loodrecht staat op de snelheid v en het magnetisch veld B. Dit verandert niet de grootte van de snelheid, maar wel de richting: de magnetische kracht buigt de baan van het deeltje af. Het uitwendig product zorgt ook voor een factor $sin (\theta) \!$ in de grootte van de kracht. Daarbij is $\theta \!$ de hoek tussen v en B

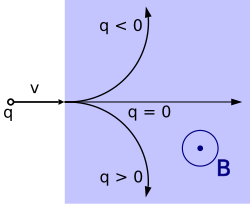
Op de afbeelding rechts is een deeltje weergegeven, met snelheid $\vec{v}$, in de achtergrond van een magnetisch veld B. Het deeltje ondervindt dus een lorentzkracht. Als de lading q positief is, werkt de kracht naar beneden zodat het deeltje in die richting afbuigt. Is q gelijk aan nul, dan is er geen lorentzkracht en gaat het deeltje rechtuit. Is q negatief, dan werkt de lorentzkracht naar boven.

Verschijningsvormen

In het algemene spraakgebruik wordt vaak alleen de magnetische component als de lorentzkracht beschouwd. In vectorvorm geldt

$\vec F_L=q \vec v \times \vec B$

Voor de grootte van de kracht geldt

$F_L = q v B sin (\theta) \!$

Wanneer men een draadraam, staafje of andere geleider in een magnetisch veld plaatst, ondervindt deze ook een lorentzkracht (ook wel Laplacekracht genoemd). Daarvoor geldt de volgende vectorvorm van de wet omdat $q \vec v = \vec I l$:

$\vec F_L= \vec I \times \vec B l$

Lorentzkracht bij een draadraam

met I de stroomsterkte (in ampère) en l de lengte van de geleider (in meter). Voor de grootte van de kracht geldt

$F_L = I B l sin (\theta) \!$

Als zich meerdere windingen binnen het magnetisch veld bevinden, wordt de kracht er evenredig mee vermenigvuldigd. In vectorvorm:

$\vec F=\vec I \times \vec B * l * n$

met n het aantal windingen. Voor de grootte van de kracht geldt

$F_L = I B l n sin (\theta) \!$

Richting

Linkerhandregel.

Een belangrijk aspect van de lorentzkracht is de richting. Deze is loodrecht op het magnetisch veld (B), en ook loodrecht op de richting van de stroomsterkte (I) (of de bewegingsrichting (v) van het geladen deeltje). De lorentzkracht werkt dus niet in de richting van het magnetisch veld. Daardoor wordt de stroomdraad ook niet per se naar de magneet of spoel getrokken die het veld veroorzaakt. Dit aspect maakt de lorentzkracht anders dan alle andere krachten.

Om de richting van de lorentzkracht te bepalen kan men de linkerhandregel gebruiken. Houdt men de gestrekte linkerhand zo, dat de veldlijnen langs de palm intreden en dat de vingertoppen gericht zijn volgens de stroomzin, dan wijst de gestrekte duim de zin aan van de beweegkracht.

Een andere manier is de FBIregel. U vormt een pistool met uw rechterhand door de wijsvinger recht vooruit te steken en een loodrechte hoek te laten vormen met uw duim. Uw duim steekt dan fier omhoog. Vervolgens wijst u met uw duim naar u toe en maakt u met de resterende vingers een loodrechte hoek met de wijsvinger. Deze wijzen dan naar links. Deze resterende vingers duiden dan de richting van de lorentzkracht aan. Uw wijsvinger geeft de richting van de magnetische veldlijnen aan, en uw duim geeft de richting van de stroomsterkte aan.

Een derde, minder gewelddadige, manier is de kurkentrekkerregel. Men draait eenvoudig een kurkentrekker van $I\!$ naar $B\!$. De kurkentrekker gaat dan vooruit de fles in. Dit is de richting van $F_L\!$.

Toepassingen

De toepassingen zijn legio:

• dynamo
• elektromotor
• beeldbuis in televisie
• synchrotron
• railgun
• massaspectroscopie
• Hall-effect

enzovoorts.

Zie ook

• Wet van Ampère
• Wet van Coulomb
• Wet van Lenz
• Wetten van Maxwell
• Inductiewet van Faraday
• Elektrolysewet van Faraday