Betegeling

Een betegeling of tessellatie van een vlak is een manier om dat vlak met tegels te bedekken, zodat zij overal aansluitend tegen elkaar en nergens over elkaar liggen. Een voorbeeld van een betegeling is de regelmatige manier waarop vloertegels op een vloer zijn gelegd.

We zien door de hele kunstgeschiedenis, van de architectuur uit de oudheid tot in de moderne kunst, betegelingen terugkomen. Een tessella was in het Latijn was een klein kubusvormig stukje van klei, steen of glas dat werd gebruikt om mozaïeken te leggen.^[1] Tessella, van tessera, betekent 'klein vierkant' en komt van het Oudgriekse τέσσερα, dat vier betekent. MC Escher maakte in zijn kunst veel gebruik van betegelingen.

Men spreekt ook van betegelingen van delen van een vlak, in meer dimensies en in een hyperbolisch vlak. Wanneer niet anders wordt vermeld, gaat het hier om betegelingen met translatiesymmetrie.

Twee dimensies

Definities

Een betegeling heet regelmatig als alle veelhoeken of tegels congruent zijn.

Een betegeling is hoekpunttransitief of isogonaal als er voor elk tweetal hoekpunten P, Q van de betegeling een isometrie bestaat die de betegeling op zichzelf afbeeldt en daarbij P op Q afbeeldt. Een nodige voorwaarde is dat in alle hoekpunten dezelfde soorten veelhoeken bij elkaar komen, in dezelfde of omgekeerde cyclische volgorde.
Een betegeling is vlaktransitief of isohedraal als er voor elk tweetal veelhoeken V, W van de betegeling een isometrie bestaat die de betegeling op zichzelf afbeeldt en daarbij V op W afbeeldt. De isohedrale en de regelmatige betegelingen zijn hetzelfde.

Een betegeling is uniform als alle tegels uitsluitend regelmatige veelhoeken zijn en de betegeling hoekpunttransitief is. De hoekpuntconfiguratie geeft daarbij aan welke veelhoeken in een hoekpunt samenkomen, bijvoorbeeld 4.8.8 als steeds een vierkant en twee regelmatige achthoeken samenkomen. Een uniforme betegeling is halfregelmatig als deze niet regelmatig is.

Regelmatige betegeling

Er zijn behoudens isometrie en schaling drie regelmatige betegelingen, namelijk met gelijkzijdige driehoeken en hoekpuntconfiguratie 3.3.3.3.3.3, in een dambordpatroon met configuratie 4.4.4.4 en in een honingraatstructuur met configuratie 6.6.6:

met gelijkzijdige driehoeken	met vierkanten in een dambordpatroon	met regelmatige zeshoeken in een honingraatstructuur

De eerste en derde zijn elkaars duale, de middelpunten van de veelhoeken van de een zijn behoudens schaling en rotatie de hoekpunten van de ander, de tweede is zelfduaal. De eerste en derde hebben dezelfde symmetriegroep.

Het aantal $n$ -hoeken die in elk hoekpunt bij elkaar komen, is

{\frac {2n}{n-2}}=2+{\frac {4}{n-2}}

Bij een regelmatige vlakvulling met regelmatige $n$ -hoeken moet $n-2$ daarom een deler zijn van 4, dus 1, 2 of 4. Dat geeft voor $n$ de mogelijkheden 3, 4 en 6.

Bij een volledige betegeling van een vlak zijn de aantallen hoekpunten, zijden en $n$ -hoeken alle drie oneindig, zodat niet zonder meer een verhouding van de drie aantallen te geven is. Een methode om dit toch te doen is per veelhoek het aantal lijnstukken en punten te corrigeren voor het delen ervan met andere veelhoeken, zoals het voor de helft meetellen van de lijnstukken aan de rand. De verhouding van het aantal hoekpunten, het aantal zijden en het aantal $n$ -hoeken komt dan op $(n-2):n:2$ . Dat is voor gelijkzijdige driehoeken, vierkanten en regelmatige zeshoeken 1:3:2, 1:2:1 en 2:3:1.

Uniforme betegeling

Er bestaan elf verschillende uniforme betegelingen, waarvan er drie regelmatig zijn en acht halfregelmatig. De acht halfregelmatige betegelingen staan hieronder afgebeeld.

3.3.3.4.4
3.3.4.3.4
3.6.3.6
3.3.3.3.6 twee gespiegelde varianten
3.4.6.4
3.12.12
4.8.8
4.6.12

Betegeling met identieke tegels

Betegelingen met identieke tegels kunnen met drie-, vier-, vijf- en zeshoeken worden gemaakt. Met alle drie- en vierhoeken kan het vlak worden gevuld. Er zijn tot nu toe vijftien convexe vijfhoeken gevonden waarmee het vlak kan worden gevuld, maar er zijn er mogelijk nog meer. Het is bewezen dat er drie soorten zeshoeken zijn waarmee het vlak kan worden gevuld, maar dat er geen veelhoeken met meer dan zes hoeken zijn, waarmee het mogelijk is.^[2]

Behangpatroongroepen

Betegelingen van het platte vlak kunnen in een of meer richtingen translatiesymmetrie hebben. Die in twee of meer richtingen kunnen op basis van hun symmetrie worden ingedeeld in behangpatroongroepen. Heeft de betegeling translatiesymmetrie over de twee vectoren $\mathbf {t} _{\mathrm {1} }$ en $\mathbf {t} _{\mathrm {2} }$ , dan is de betegeling ook symmetrisch over de vector die een lineaire combinatie $a_{1}\mathbf {t} _{1}+a_{2}\mathbf {t} _{2}$ is van deze twee met $a_{1}$ en $a_{2}\in \mathbb {Z}$ . Er bestaan 17 behangpatroongroepen, die er alle 17 in het Alhambra in Granada in Spanje zijn. Twee van de drie regelmatige betegelingen worden met p6m aangegeven en een met p4m.

Een betegeling met translatiesymmetrie in twee of meer richtingen kan het vlak op meerdere manieren verdelen in oneindig veel identieke eenheidscellen in dezelfde stand op basis van alleen de translatiesymmetrie. Als het aantal lijnstukken, punten en vlakken van de eenheidscel wordt gecorrigeerd voor het delen ervan met andere exemplaren van de eenheidscel, zoals bijvoorbeeld het voor de helft meetellen van een lijnstuk aan de rand, en het voor een derde meetellen van een tegel die voor een derde binnen de eenheidscel ligt, dan is per eenheidscel het aantal lijnstukken gelijk aan het aantal punten plus het aantal veelhoeken waarin de eenheidscel wordt verdeeld. Bij bijvoorbeeld het dambordpatroon kunnen de vierkanten elk als eenheidscel genomen worden. Dan telt een vierkant voor één vlak, tellen de vier hoekpunten ieder voor een kwart, dus samen voor één hoekpunt, en tellen de vier zijden elk voor een half, dus samen twee zijden. Een en ander geldt overeenkomstig bij tegels die geen veelhoekvorm hebben, maar een gekromde begrenzing. De punten waar drie of meer tegels samenkomen wordt dan geteld als hoekpunt, en de rand van een tegel tussen twee van zulke punten als zijde.

Drie dimensies

Het is mogelijk veelvlakken in drie dimensies zonder ruimteverlies te stapelen. Met een beperkt aantal veelvlakken, waarbij gelijkvormige veelvlakken ook congruent zijn, zijn er onder andere de volgende mogelijkheden voor een volledige ruimtevulling:

ruimtevulling in drie dimensies'
nummer	veelvlakken	afbeelding
regelmatige veelvlakken en archimedische lichamen
1	regelmatig achtvlak en viervlak
2	kuboctaëder en regelmatig achtvlak
3	kubus
4	romboëdrische kuboctaëder, kubus en viervlak
5	romboëdrische kuboctaëder, kuboctaëder en kubus
6	afgeknotte octaëder
7	afgeknotte tetraëder en viervlak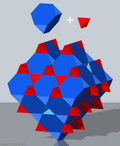
8	afgeknotte octaëder, afgeknotte tetraëder en kuboctaëder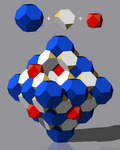
9	grote rombische kuboctaëder, afgeknotte octaëder en kubus
10	afgeknotte kubus en regelmatig achtvlak
11	afgeknotte kubus, grote rombische kuboctaëder en afgeknotte tetraëder
meer
12	rombische dodecaëder
13	grote rombische kuboctaëder en achtprisma
14	achtvlakken Deze achtvlakken zijn geen regelmatige achtvlakken.
15	verlengde vierkante bipiramide Deze verlengde vierkante bipiramides zijn niet gelijkvormig met het johnsonlichaam J₁₅.
16	gyrobifastigium
	en meer, bijvoorbeeld met een samengesteld achtvlak

Eenheidscellen zijn in de kristallografie gedefinieerd. De vorm van de eenheidscel bepaalt de structuur van een kristal. Een eenheidscel in een kristal is de kleinst mogelijke eenheid, die wanneer die in de drie verschillende mogelijke richtingen wordt gekopieerd, de ruimte volledig vult en zo het kristal vormt. De ruimtevulling met eenheidscellen is iets anders dan de ruimtevulling, die hierboven is genoemd.

Zonder translatiesymmetrie

De penrose-betegelingen zijn de bekendste betegelingen in twee dimensies zonder translatiesymmetrie, maar die zijn wel rotatiesymmetrisch. Betegelingen zonder translatiesymmetrie kunnen als model voor de structuur van quasikristallen worden gebruikt. Dit werd in 1982 door D Shechtman ontdekt.

Wetenswaardigheden

De Tessella zijn ook een geslacht van vlinders.

literatuur

HSM Coxeter. Regular Polytopes, 1973. ISBN 0-486-61480-8.
B Grunbaum en GC Shephard. Tilings and Patterns, 1987. ISBN 0-7167-1193-1.

voetnoten

↑ tessellate
↑ A vd Brandhof voor het NRC Handelsblad. De vijftiende vlakvullende vijfhoek, 14 augustus 2015.

websites

(en) The mathematical art of M. C. Escher. gearchiveerd

Zie de categorie Tilings van Wikimedia Commons voor mediabestanden over dit onderwerp.

[1] tessellate

[2] A vd Brandhof voor het NRC Handelsblad. De vijftiende vlakvullende vijfhoek, 14 augustus 2015.

[1]

[2]