Homomorfisme

Niet te verwarren met homeomorfisme, een begrip uit de topologie

In het algemeen verstaat men onder een homomorfisme een afbeelding van een verzameling met een algebraïsche structuur in een andere verzameling met een algebraïsche structuur van dezelfde soort (bijvoorbeeld twee groepen, twee ringen, of twee vectorruimten met hetzelfde scalairenlichaam), waarbij die afbeelding compatibel is met de structuren, dus de structuur van het domein overvoert in de structuur van het codomein.

Bewerkingen in de ene verzameling hebben dus een overeenkomende bewerking in de andere verzameling, waarbij het geen verschil maakt of als eerste de bewerking wordt uitgevoerd, dan wel als eerste de overstap naar de andere verzameling gemaakt wordt.

Bijvoorbeeld bij structuren met één binaire operatie komt dat neer op het volgende.

Als $f_{hom}:V\to W$ een homomorfisme is van verzameling $V$ met structuur $S_{bin}$ (de binaire operatie in $V$) in verzameling $W$ met structuur $T_{bin}$ (de binaire operatie in $W$) geldt voor alle $x,y\in V$:

$f_{hom}(S_{bin}(x,y))=T_{bin}(f_{hom}(x),f_{hom}(y))$

Voorbeelden

De logaritme ($f$) is een homomorfisme van de positieve reële getallen met als structuur de vermenigvuldiging ($S$), in de reële getallen met als structuur de optelling ($T$). Er geldt immers:

$\log(x\cdot y)=\log x+\log y$

Dit is de basis voor de decibelschalen en het rekenen met rekenliniaal of logaritmetafel: vermenigvuldigen kan omgezet worden in optellen.

Een afbeelding tussen twee groepen $h\colon G\to G'$ met groepsoperaties respectievelijk $\cdot$ en $*$ is een homomorfisme als voor ieder tweetal elementen $a,b$ uit de groep $G$ geldt:

$h(a\cdot b)=h(a)*h(b)$

Informele discussie

Omdat de abstracte algebra verzamelingen met operaties bestudeert, die interessante structuren of eigenschappen op deze verzameling genereren, zijn de interessantste functies diegene die operaties bewaren. Zulke functies staan bekend als homomorfismen.

Beschouw bijvoorbeeld de natuurlijke getallen met optellen als operatie. Een functie die een optelling bewaart moet de eigenschap hebben dat: :$f(a+b)=f(a)+f(b)$

De functie $f(x)=3x$ is bijvoorbeeld zo'n homomorfisme, aangezien

$f(a+b)=3(a+b)=3a+3b=f(a)+f(b)$

Merk op dat dit homomorfisme de natuurlijke getallen afbeeldt in zichzelf.

Homomorfismen hoeven niet noodzakelijk een afbeelding te zijn tussen verzamelingen die dezelfde operaties hebben. Er bestaan bijvoorbeeld operatie-bewarende functies tussen de verzameling van de reële getallen met de operatie optelling en de verzameling van de positieve reële getallen met de operatie vermenigvuldiging. Een functie die een operatie bewaart, vereist hier dan de eigenschap dat: $f(a+b)=f(a)\cdot f(b)$, aangezien optelling de operatie in de eerste verzameling en vermenigvuldiging de operatie in de tweede verzameling is. Gegeven de wetten van het machtsverheffen, voldoet $f(x)=e^{x}$ aan deze voorwaarde:

$f(a+b)=e^{a+b}=e^{a}e^{b}=f(a)\cdot f(b)$

Een bijzonder belangrijke eigenschap van homomorfismen is dat wanneer een identiteitselement aanwezig is, dit altijd bewaard zal blijven. Dit neutrale element wordt namelijk op zichzelf afgebeeld. Merk op dat in het eerste voorbeeld $f(0)=0$ en dat 0 dan de additieve identiteit is. In het tweede voorbeeld is $f(0)=1$, aangezien 0 hier de additieve identiteit, en 1 de multiplicatieve identiteit is.

Als we meerdere operaties op een verzameling in overweging nemen, moeten alle operaties bewaard blijven, wil een functie als homomorf worden gezien. Eenzelfde functie, kan bijvoorbeeld in de groepentheorie (verzamelingen met één enkele operatie) homomorf zijn, terwijl dezelfde functie in de ringtheorie (verzamelingen met twee gerelateerde operaties) niet homomorf is, bijvoorbeeld omdat deze functie de extra operatie, die in ringtheorie wordt bestudeerd, niet bewaart.

Soorten homomorfismen

• Een isomorfisme is een bijectief homomorfisme. Van twee objecten wordt gezegd dat ze isomorf zijn als er een isomorfisme tussen deze twee objecten bestaat. Isomorfe objecten zijn, wat de structuur in kwestie betreft, niet van elkaar te onderscheiden.

• Een epimorfisme is een surjectief homomorfisme.

• Een monomorfisme (ook wel aangeduid als een uitbreiding) is een injectief homomorfisme.

• Een endomorfisme is een homomorfisme van een object naar zichzelf.

• Een automorfisme is een endomorfisme dat tegelijkertijd ook een isomorfisme is.

De bovenstaande termen worden op soortgelijke wijze in de categorietheorie gebruikt, in de categorietheorie zijn de definities echter meer subtiel, zie het artikel over morfisme voor meer details.

Merk op dat in de ruimere context van de structuur-bewarende afbeeldingen, het in het algemeen niet genoeg is om een isomorfisme als een bijectief morfisme te definiëren. Men dient ook te eisen dat de inverse een morfisme van hetzelfde type is. In een algebraïsche omgeving (tenminste binnen de context van de universele algebra) wordt automatisch aan deze extra voorwaarde voldaan.

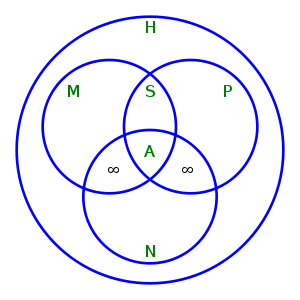
Relaties tussen de verschillende soorten homomorfismen.
H = verzameling van Homomorfismen, M = verzameling van Monomorfismen,
P = verzameling van ePimorfismen, S = verzameling van iSomorfismen,
N = verzameling van eNdomorfismen, A = verzameling van Automorfismen.
Merk op dat: (M ∩ P) = S, (S ∩ N) = A, (M ∩ N) \ A en (P ∩ N) \ A alleen homomorfismen van oneindige algebraïsche structuren naar zichzelf bevatten.

Zie ook

• automorfisme
• endomorfisme
• epimorfisme
• homeomorfisme
• isomorfisme
• monomorfisme
• morfisme