Poissonverdeling
| Poissonverdeling | ||||
|---|---|---|---|---|
Kansfunctie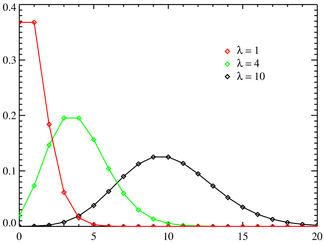
| ||||
Verdelingsfunctie De horizontale as is in beide figuren de index . Merk op dat de kansfunctie, dus ook de verdelingsfunctie, alleen voor gehele waarden van is gedefinieerd. Het verbinden van de lijnen duidt niet op continuïteit. | ||||
| Parameters | ||||
| Drager | ||||
| Kansfunctie | ||||
| Verdelingsfunctie | ||||
| Verwachtingswaarde | ||||
| Mediaan | N/A | |||
| Modus | ||||
| Variantie | ||||
| Scheefheid | ||||
| Kurtosis | ||||
| Entropie | ||||
| Moment- genererende functie |
||||
| Karakteristieke functie | ||||
| ||||
De poissonverdeling is een discrete kansverdeling die met name van toepassing is bij het tellen van bepaalde voorvallen gedurende een gegeven tijdsinterval, afstand, oppervlakte, volume etc. De poissonverdeling is genoemd naar Siméon Poisson, die deze kansverdeling ontdekte en samen met zijn statistische theorie in 1838 publiceerde in zijn werk Recherches sur la probabilité des jugements en matières criminelles et matière civile.
Als de stochastische variabele het aantal voorvallen telt gedurende een gegeven interval van tijd, plaats, afstand , e.d., dan is volgens de poissonverdeling de kans dat er precies voorvallen plaatsvinden, met een natuurlijk getal:
Hierin is:
- het grondtal van de natuurlijke logaritme, ,
- de faculteit van ,
- een positief reëel getal, gelijk aan het verwachte aantal voorvallen in het interval. Als er bijvoorbeeld 1 voorval elke 2 minuten wordt verwacht, en het tijdsinterval is 10 minuten, dan kan een poissonverdeling met als model worden gebruikt.
Poissonproces[bewerken | brontekst bewerken]
Soms wordt iets anders gebruikt, namelijk als het verwachte aantal voorvallen per tijdseenheid. In dat geval is, met het aantal voorvallen dat optreedt vóór tijdstip :
- ,
en de wachttijd tot het eerste voorval is een continue stochastische variabele met een exponentiële verdeling. Deze verdeling kan worden afgeleid uit het gegeven dat
Als men de tijd erbij betrekt, heeft men een eendimensionaal poissonproces, waarin men zowel de discrete poissonverdeelde toevalsgrootheden heeft die het aantal aankomsten in elk tijdsinterval tellen, als de continue erlang-gedistribueerde wachttijden. Er bestaan ook poissonprocessen met een graad groter dan een.
Voorkomen in de praktijk[bewerken | brontekst bewerken]
De poissonverdeling komt voor in relatie met zogenaamde poissonprocessen. Zij is van toepassing op diverse fenomenen die een discrete aard hebben, dat wil zeggen dat ze 0, 1, 2, 3... keer voorkomen gedurende een gegeven tijdsinterval of in een bepaald gebied, als de kans op een gebeurtenis constant is in de tijd of in de ruimte. Voorbeelden zijn:
- het aantal atoomkernen die binnen een bepaalde tijd in een stuk radioactief materiaal vervallen
- het aantal auto's die gedurende een zekere tijd een bepaald punt van een weg passeren. Dit geldt niet als het zo druk is dat er twee of meer tegelijk voorbijkomen!
- het aantal door een secretaresse gemaakte typefouten bij het typen van een enkele pagina
- het aantal telefoontjes die iemand op een dag krijgt
- het aantal keren per jaar dat een taalkundige discussie opvlamt
- het aantal keren in een minuut dat een webserver wordt benaderd
- het aantal in een uur gewijzigde pagina's op Wikipedia
- het aantal dode dieren op een kilometer weg
- het aantal mutaties in een stuk DNA van gegeven lengte na een bepaalde stralingsdosis
- het aantal naaldbomen op een hectare gemengd bos
- het aantal sterren in een gegeven ruimte
- het aantal bommen die op een vierkante mijl van Londen vielen gedurende een Duitse luchtaanval in het begin van de Tweede Wereldoorlog
Verband met de binomiale verdeling[bewerken | brontekst bewerken]
De poissonverdeling kan afgeleid worden als limietgeval van een binomiale verdeling met parameters en , als naar oneindig gaat. Dat is de kansverdeling van het aantal successen uit , met als kans op succes voor elke poging. Laat binomiaal verdeeld zijn met parameters en , dan is
want
Eigenschappen[bewerken | brontekst bewerken]
- De verwachtingswaarde voor een poisson-verdeelde stochastische variabele X is gelijk aan , en de variantie ook.
- dus
- De meest waarschijnlijke waarde, de modus, van een poisson-verdeelde stochastische variabele is voor niet-gehele waarden van gelijk aan het grootste gehele getal kleiner dan . Voor gehele waarden van zijn er twee modi, zowel als . Vergelijk daartoe de kansen voor en ; het quotiënt daarvan is:
dus
- Voor grote , zeg , is de normale verdeling met verwachting en variantie een goede benadering van de poissonverdeling. Voor andere, niet te kleine waarden van (zeg ), is de normale verdeling een goede benadering als een continuïteitscorrectie wordt toegepast. Kansen voor een poisson-verdeelde X worden benaderd met de verdeling van Y die -verdeeld is:
- Als en twee onderling onafhankelijke stochastische variabelen zijn die beide een poissonverdeling hebben met respectievelijk parameters en , dan geldt dat een poissonverdeling heeft met parameter . Er geldt:










![{\displaystyle \lambda [1\!-\!\ln(\lambda )]\!+\!e^{-\lambda }\sum _{k=0}^{\infty }{\frac {\lambda ^{k}\ln(k!)}{k!}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24650c837524f593a60e41f7371b39de75512d5c)

















![{\displaystyle {\begin{aligned}P(X_{n}=k)&={n! \over k!(n-k)!}\left({\lambda \over n}\right)^{k}\left(1-{\lambda \over n}\right)^{n-k}\\&=\left[{\frac {n!}{n^{k}\left(n-k\right)!}}\right]{\frac {\lambda ^{k}}{k!}}\underbrace {\left(1-{\frac {\lambda }{n}}\right)^{n}} _{\to \exp \left(-\lambda \right)}\underbrace {\left(1-{\frac {\lambda }{n}}\right)^{-k}} _{\to 1}\to {\frac {\lambda ^{k}}{k!}}e^{-\lambda }\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0cb781a677bc692b5d57ada668a67e07926b1362)


















