Elliptische kromme
In de meetkunde zijn elliptische krommen een speciale soort algebraïsche krommen waarop meetkundig een optelling gedefinieerd is. De naam is ontleend aan de ellips, maar het verband is slechts zijdelings en ellipsen zijn heel uitdrukkelijk geen voorbeelden van elliptische krommen.
Elementaire definitie[bewerken | brontekst bewerken]
Een elliptische kromme is een verzameling punten van het vlak waarvan de coördinaten voldoen aan een vergelijking van de vorm
met een polynoom van de derde graad zonder samenvallende nulpunten, die na een eventuele lineaire transformatie over te voeren is in:
met en zo, dat de polynoom geen dubbele nulpunten heeft.
Als onder het "vlak" de reële euclidische ruimte wordt verstaan, kan een elliptische kromme grafisch worden voorgesteld in een van de volgende twee gedaanten (naargelang de polynoom drie reële nulpunten of slechts één reëel nulpunt heeft):
Meestal worden elliptische krommen echter beschouwd over de complexe tweedimensionale ruimte , of zelfs over het complexe projectieve vlak . In dat laatste geval wordt de vergelijking gehomogeniseerd met een derde veranderlijke :
Over het complexe projectieve vlak zijn alle elliptische krommen topologisch gelijkwaardig (homeomorf) met de torus, en dus ook met elkaar.
Alternatieve definitie[bewerken | brontekst bewerken]
Een elliptische kromme is het Riemann-oppervlak dat ontstaat als quotiëntruimte van het complexe vlak over een rooster, d.i. een discrete deelgroep van de vorm
Hoewel alle elliptische krommen topologisch gelijkwaardig zijn, zijn ze niet allemaal gelijkwaardig als Riemann-oppervlak. Elke elliptische kromme is echter biholomorf (equivalent als Riemann-oppervlak) met een elliptische kromme waarvoor en waarvoor het imaginaire deel van strikt positief is.
Het verband met de elementaire definitie wordt gegeven door de -functie van Weierstrass en haar afgeleide. Dat is een dubbelperiodieke meromorfe functie op het complexe vlak met polen van de tweede orde in de punten van het rooster . Ze voldoet aan
Hierin zijn de constanten () de sommen van de Eisenstein-reeksen van het rooster.
Het geordende paar parametriseert een complexe elliptische kromme in de elementaire zin. Omgekeerd blijkt elke complexe elliptische kromme afkomstig te zijn van de Weierstrass-functie van een rooster.
Groepsbewerking[bewerken | brontekst bewerken]
Op een elliptische kromme bestaat een natuurlijke abelse groepsbewerking. Bij de alternatieve definitie is dit gewoon de factorgroep die ontstaat uit de optelling van complexe getallen. Bij de elementaire definitie aan de hand van een polynoom heeft de groepsbewerking meetkundig de volgende vorm.
Omdat een elliptische kromme symmetrisch is ten opzichte van de x-as, ligt van elk punt op de kromme ook het spiegelbeeld ten opzichte van de x-as, de gespiegelde, op de kromme.
Een elliptische kromme in het complexe projectieve vlak snijdt de rechte op oneindig in één punt met als projectieve coördinaten . Dit punt vertegenwoordigt de richting evenwijdig aan de y-as.
Van twee verschillende punten en op een elliptische kromme (in het complexe projectieve vlak) snijdt de rechte door de kromme in precies één derde punt . In het geval dat en elkaars gespiegelde zijn, ligt dit punt op oneindig. De som is gedefinieerd als de gespiegelde van dit derde punt .
Als en samenvallen, neemt men voor het snijpunt van de raaklijn aan de kromme.
Als het punt op oneindig is, neemt men de rechte door in de richting van als verbindingslijn.
Daarmee is duidelijk dat voor alle punten en de som welgedefinieerd is als een punt op de kromme en dat de optelling commutatief is: .
Voor alle punten geldt: , dus is het neutrale element.
Voor de gespiegelde van een punt volgt dus is de tegengestelde van . Voor het snijpunt van de rechte door en met de kromme geldt dus: . Voor de drie snijpunten van een rechte met de kromme geldt dus:
De associativiteit van de optelling is geen voor de hand liggende eigenschap. Met behulp van de stelling van Cayley-Bacharach kan het bewijs gemakkelijk gegeven worden (zie de figuur).

De drie punten, en liggen op een elliptische kromme. De drie rechten en , en de drie rechten en hebben negen snijpunten:
Daarvan liggen de eerste acht op de elliptische kromme. Maar dan ligt volgens de stelling ook het negende snijpunt, dat van en , op de kromme. Dus is , of anders geschreven: .
Een rationale elliptische kromme bestaat uit punten waarvan de projectieve coördinaten rationale getallen zijn, en voldoen aan een vergelijking zoals hierboven. De coëfficiënten van de derdegraadspolynoom moeten eveneens rationale getallen zijn.
Analytisch[bewerken | brontekst bewerken]
Als de punten en van elkaar verschillen en gegeven zijn in een xy-assenstelsel, wordt de som gegeven door:
met
de richtingscoëfficiënt van de lijn door en .
Er geldt namelijk :
dus:
Verder is voor de kromme
Ook is
Analoog geldt:
Aftrekken levert
dus
Als , is en is .
In het geval dat en , krijgt de waarde van de richtingscoëfficiënt van de raaklijn in . Is dan is en is de som het punt op oneindig (0).
Rationale elliptische kromme[bewerken | brontekst bewerken]
De stelling van Mordell luidt dat een rationale elliptische kromme, opgevat als abelse groep, eindig voortgebracht is. Er bestaat dus een eindige deelverzameling van waaruit ieder willekeurig punt op de kromme door een eindig aantal sommen kan worden bereikt.
Endomorfismen[bewerken | brontekst bewerken]
Omdat een elliptische kromme met de groepsbewerking 'optelling' een abelse groep is, vormen de endomorfismen een ring, aangeduid met of . Deze ring kan drie vormen hebben (isomorf): de gehele getallen , een speciale deelring in een kwadratisch lichaam (Ned) / veld (Be) of in een quaternionen-algebra over .
De ring van elke elliptische kromme bevat als deelring. De endomorfismen in deze deelring worden daarom wel de triviale endomorfismen genoemd. Als er meer endomorfismen zijn zegt men dat de kromme complexe vermenigvuldiging heeft.
Als het lichaam/veld eindig is, zijn er altijd niet-triviale endomorfismen, afkomstig van het frobenius-endomorfisme; al zulke krommen hebben dus een complexe vermenigvuldiging. Maar als het basislichaam/veld een getallenlichaam/veld is, is complexe vermenigvuldiging een uitzondering.
Naamgeving[bewerken | brontekst bewerken]
Elliptische krommen spelen een rol bij de studie van elliptische functies die ontstaan uit de integralen waarmee de omtrek van delen van een ellips kan worden berekend.
Toepassingen[bewerken | brontekst bewerken]
Elliptische krommen zijn bestudeerd als interessante objecten op zich, omdat ze de eerste stap van de meetkunde "voorbij" de kegelsneden zijn. Ze hebben echter toepassingen gevonden in andere gebieden van de wiskunde, en met name de getaltheorie heeft in 1995 een spectaculair succes geboekt door aan de hand van elliptische krommen de laatste stelling van Fermat te bewijzen.
Referenties[bewerken | brontekst bewerken]
- James Milne (2006), Elliptic Curves. Booksurge Publishing. ISBN 1-4196-5257-5.
- Joseph H. Silverman (1985), The Arithmetic of Elliptic Curves. Springer Graduate Texts in Mathematics vol.106. ISBN 0-387-96203-4.







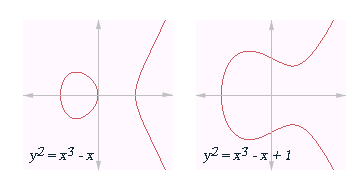














![{\displaystyle [0:1:0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ddb225ddb544b9183ae37507e364ab290e5c14b8)



























































