Zwart gat

Zwart gat in het centrum van het sterrenstelsel M87. Kleurenweergave samengesteld uit waarnemingen met radiotelescopen, aangeduid als de "eerste foto van een zwart gat", april 2019.

Een artistieke impressie van een zwart gat met een begeleiderster (geel) die zijn Rochelob gevuld heeft. Gas uit de begeleider valt naar het zwarte gat en vormt een accretieschijf (blauw). Een deel wordt haaks met veel energie uitgespuwd aan beide polen.

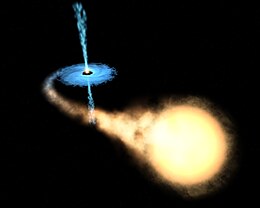
Volgens de algemene relativiteitstheorie is een zwart gat een gebied in de astronomische ruimte waaruit niets – geen deeltjes en zelfs geen licht – kan ontsnappen. Dit is het gevolg van een extreme vervorming van de ruimtetijd die hier optreedt, door de zwaartekracht van een zeer compacte enorme massa.

Rondom een zwart gat is er een denkbeeldig oppervlak dat als grens fungeert, de zogeheten waarnemingshorizon. Vlak buiten deze waarnemingshorizon kan het licht nog net wel aan de enorme zwaartekracht ontsnappen. Volgens de kwantumveldentheorie is de waarnemingshorizon de plaats waar hawkingstraling wordt gevormd.

Zwarte gaten ontstaan wanneer zeer zware sterren aan het einde van hun levensloop ineenstorten. Nadat het zwarte gat is gevormd, neemt het meestal toe in grootte door materie uit de omgeving op te nemen. Wanneer een zwart gat samensmelt met andere zwarte gaten, kan er een superzwaar zwart gat ontstaan met een massa van miljarden zonsmassa's (M_☉). Aangenomen wordt dat de meeste sterrenstelsels een superzwaar zwart gat in hun centrum hebben.

De aanwezigheid van een zwart gat kan worden afgeleid uit de interactie met andere materie en met elektromagnetische straling zoals zichtbaar licht. Materie die langs een zwart gat beweegt, kan bijvoorbeeld verstrooid worden tot een karakteristieke accretieschijf. Ook sterren die rondom een zwart gat draaien zijn mogelijke aanwijzingen: hun baan kan worden gebruikt om de massa en locatie van het zwarte gat te bepalen.

Geschiedenis van het onderzoek naar zwarte gaten

Deze opname laat in valse kleuren het centrum van de Melkweg zien. De heldere punt in het midden is een uitbarsting van röntgenstraling in de buurt van Sagittarius A^*. De stralingsintensiteit nam in enkele minuten extreem toe, hield ongeveer 3 uur aan om daarna snel uit te doven. Waarschijnlijk betrof het hier gas dat in het zwarte gat viel.

De röntgenstraling die gedetecteerd werd in het gebied binnen de cirkels duidt op zwarte gaten in het centrum van een ver sterrenstelsel. De stelsels zijn hier te zien in zichtbaar en infrarood licht en het blijkt dat de infrarode beelden van twee bronnen helderder zijn, waarschijnlijk omdat infrarode straling minder geblokkeerd wordt door stof tussen de bron en de waarnemer.

De eerste ideeën over het bestaan van zwarte gaten dateren uit 1790, toen de Engelse geoloog John Michell en de Franse wiskundige Pierre-Simon Laplace onafhankelijk van elkaar het bestaan van onzichtbare sterren veronderstelden. Ze berekenden aan de hand van de wetten van Newton de massa en de omvang van objecten waarvan de ontsnappingssnelheid groter zou zijn dan de lichtsnelheid.

Het idee dat het voor materie onmogelijk zou kunnen zijn om aan nabijgelegen objecten te ontsnappen had in die tijd nog geen enkele concrete onderbouwing. Dat de lichtsnelheid de maximale snelheid is, werd pas in 1905 aannemelijk gemaakt door Albert Einstein in zijn speciale relativiteitstheorie.

In 1916 publiceerde Einstein de algemene relativiteitstheorie, een nieuwe theorie over de zwaartekracht. Enkele maanden later vond Karl Schwarzschild het door de relativiteitstheorie voorspelde zwaartekrachtsveld voor een puntmassa, waaruit de theoretische mogelijkheid van een waarnemingshorizon bleek. Schwarzschild zelf beschouwde deze horizon niet als fysisch realistisch; de waarnemingshorizon bleek later echter wel degelijk betekenis te hebben en wordt tegenwoordig geïnterpreteerd als de "rand" van het zwarte gat.

J. Robert Oppenheimer (de latere uitvinder van de Amerikaanse atoombom) en zijn student H. Snyder kwamen in 1939 met de eerste nauwkeurige berekening van de vorming van een zwart gat uit een gasbol volgens de algemene relativiteitstheorie.

Roy Kerr vond in 1963 een familie van exacte oplossingen van Einsteins vergelijkingen zonder elektrische lading die later op zwarte gaten betrekking bleken te hebben. Deze oplossingen beschrijven roterende zwarte gaten. Algemene oplossingen voor de Einstein-Maxwell-vergelijkingen met rotatie én lading werden daarna gevonden door Newman en anderen in 1965. Met de Kerr-Newman-geometrie kunnen draaiende (on)geladen zwarte gaten worden beschreven.

In 1967 introduceerde de Amerikaanse theoretisch natuurkundige John Wheeler – die eerder onder meer aan de waterstofbom had gewerkt – de benaming black hole voor dergelijke objecten, in het Nederlands vertaald als "zwart gat". De bondige uitspraak "Een zwart gat heeft geen haar" (no-hair theorem: A black hole has no hair) staat ook op zijn naam, maar volgens Wheeler had hij hem gehoord van Jacob Bekenstein. Wheeler bedoelde hiermee dat een zwart gat eigenlijk een eenvoudig object is. Alle eigenschappen zijn af te leiden uit zijn massa, elektrische lading en impulsmoment. Twee, of meerdere, zwarte gaten met gelijke waarden voor deze parameters zijn dus identiek aan elkaar.

Met behulp van de zwaartekrachtgolf-detector LIGO zijn sinds 2015 een aantal samensmeltingen van zwarte gaten geregistreerd.

Op 10 april 2019 werd bekend dat astronomen er met behulp van de Event Horizon Telescope (EHT), een virtuele radiotelescoop zo groot als de Aarde, er voor het eerst in geslaagd waren om een echte foto te maken van een zwart gat. Het ging in feite om een beeld van de fotonengordel rond de waarnemingshorizon van het superzware zwarte gat in het sterrenstelsel M87, en van de schaduw van die horizon.

Relativistische modellering

Simulatie van een zwaartekrachtlens ten gevolge van een zwart gat dat het beeld van een passerend sterrenstelsel in de achtergrond vervormt en even een ring van licht veroorzaakt. Bij echte waarnemingen gaat het vaak om kleinere beeldjes van sterrenstelsels en quasars dan in deze simulatie.

Het eenvoudigste model van een zwart gat gaat uit van de ineenstorting van een bolsymmetrische, elektrisch neutrale ster. De vierdimensionale metriek in de omgeving wordt dan beschreven door de formule

$ds^{2}=-(1-2M/r)dt^{2}+{\frac {dr^{2}}{1-2M/r}}+r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2})$

Het oppervlak van het zwarte gat (de horizon) bevindt zich op afstand $r=2M$ en alleen het gebied met $r\geq 2M$ is relevant voor uitwendige waarnemers.

Hierbij zijn, zoals wel vaker gebeurt in teksten over de relativiteitstheorie, de eenheden speciaal geijkt zodat de lichtsnelheid $c$ en de gravitatieconstante $G$ gelijk zijn aan de dimensieloze constante 1; energieën, massa's en afstanden worden in dezelfde eenheid uitgedrukt en dus wordt $r$ vergelijkbaar met $2M.$ In de paragraaf inval door de waarnemingshorizon hieronder wordt de straal van de waarnemingshorizon in conventionele eenheden uitgedrukt, met $c$ en $G$ op de juiste plaats.

No-hair theorem

In een realistischer benadering zal de ineenstortende ster afwijken van de bolvorm en een nettolading hebben die lichtjes verschilt van 0; maar zelfs dan wordt het zwarte gat volledig beschreven door de drie parameters:

1. massa $M,$
2. elektrische lading $Q$ en
3. impulsmoment $S.$

Dit staat bekend als het no-hair theorem ("zwarte gaten zijn kaal"). Zwarte gaten zijn daarmee de "eenvoudigste" objecten uit de natuurkunde.

De redenen voor het no-hair theorem kunnen heuristisch als volgt worden uitgelegd. Van alle grootheden die een geïsoleerde bron van lading en elektromagnetisme kenschetsen, laten alleen $M,$ $Q$ en $S$ unieke, permanente sporen na in de verafgelegen velden. Wanneer een ster ineenklapt en een zwart gat vormt, worden de verafgelegen uitwendige velden gedwongen deze drie grootheden te behouden. Alle andere invloeden zoals de interne verdeling van massa, lading en stroom, worden effectief afgesloten van de buitenwereld. Daardoor relaxeren de uitwendige velden na verloop van tijd tot een stationaire toestand die alleen van de drie basisparameters afhangt (na het eventueel uitzenden van zwaartekracht- en elektromagnetische golven).

Eigenschappen

Indeling

Naar massa en omvang

Er worden naar massa en omvang vier soorten zwarte gaten onderscheiden:

• Minuscule zwarte gaten: met afmetingen van minimaal die van een planckdeeltje (10⁻³⁵ meter) tot maximaal 0,1 millimeter en een massa die varieert van de planckmassa (±0,02 milligram) tot die van pakweg onze Maan. Dit soort zwarte gaten is vooralsnog geheel theoretisch; er is geen enkel bewijs dat ze echt bestaan. De kleinste exemplaren, als deze echt (hebben) bestaan, zouden door de hawkingstraling in een fractie van een seconde verdampen. Dit type zwart gat is volgens Stephen Hawking niet ontstaan door zijn eigen zwaartekracht, maar door druk van buitenaf en zou tijdens of kort na de oerknal kunnen hebben bestaan. Als blijkt dat de planckschaal in de orde van TeV is, is het mogelijk om in de Large Hadron Collider dit soort zwarte gaten te produceren. Dan zouden verschillende kosmologische theorieën experimenteel getest kunnen worden. Volgens sommige theorieën bestaat het kwantumschuim eveneens uit minuscule zwarte gaten die volgens de onzekerheidswetten inherent aan de kwantumwereld voortdurend in en uit de virtuele ruimte schieten.
• Stellaire zwarte gaten: met een massa van omstreeks 5 tot 100 zonsmassa's, die ontstaan zijn uit een supernova van een zware ster.
• Middelzware zwarte gaten: met een massa van 500 tot 1000 zonsmassa's. Over de evolutie van dit soort zwarte gaten is nog weinig bekend. Dit type werd door de Chandra X-ray Observatory ontdekt in het stelsel M82 op een afstand van 600 lichtjaar van het centrum. Bij het melkwegstelsel ESO 243-49 (met roodverschuiving z = 0,0224) werd met de XMM-Newton satelliet het zwarte gat 2XMM J011028.1-460421 (HLX-1) gevonden met een massa van minstens 500 zonsmassa's.
• Superzware zwarte gaten: met een massa van vijftigduizend tot vele miljoenen malen de massa van de zon. Ze worden aangetroffen in de centra van sterrenstelsels.

In tabelvorm weergegeven (M_Maan is hier de massa van de Maan, M_Zon is de massa van de Zon, R_Aarde is de straal van de Aarde = 6378 km, en AU = astronomische eenheid = 149,6×10⁹ m, ongeveer de gemiddelde afstand tussen de Aarde en de Zon):

Soort zwart gat	Massa	Grootte
Miniatuur	tot ~MMaan	tot ~0,1 mm
Stellair	~10 MZon	~30 km
Middelzwaar	~103 MZon	~103 km ~ RAarde
Superzwaar	~105–109 MZon	~0,001–400 AU

Naar impulsmoment en lading

Er kunnen vier soorten zwarte gaten worden onderscheiden op grond van hun impulsmoment (J) en elektrische lading (Q). Als J > 0 draait het zwarte gat. De massa (M) is altijd positief. De meetkundevarianten (metrieken) waarmee deze soorten beschreven worden, staan in bijgaande tabel. De schwarzschildmetriek beschrijft een ongeladen, niet-draaiend zwart gat. Het is de oplossing van de einstein-vergelijkingen in vacuüm met bolsymmetrie.

De Kerrmetriek beschrijft een ongeladen, draaiend zwart gat.

	M > 0
	J = 0	J ≠ 0
Q = 0	Schwarzschildmetriek	Kerrmetriek
Q ≠ 0	Reissner-Nordströmmetriek	Kerr-Newmanmetriek

Inval door de waarnemingshorizon

Zie Waarnemingshorizon voor het hoofdartikel over dit onderwerp.

Ver van een zwart gat is een deeltje vrij om te bewegen in een willekeurige richting, zij het met een snelheid kleiner dan die van het licht.

Dichter bij het zwarte gat begint de tijdruimte te vervormen. Meer mogelijke banen leiden naar het zwarte gat toe dan er vanaf.

Binnen de waarnemingshorizon (event horizon) leiden alle mogelijke banen naar het midden van het zwarte gat: er is geen ontsnappen aan.

Kenmerkend aan een zwart gat is de waarnemingshorizon - de grens in de tijdruimte die als een ventiel voor licht en materie werkt: die kunnen er alleen van buiten naar binnen doorheen. Waarneming van wat binnen de waarnemingshorizon geschiedt is dus onmogelijk van buitenaf. Tevens kan er van binnenuit het zwarte gat geen enkel signaal naar buiten worden verstuurd.

De algemene relativiteitstheorie voorspelt dat een grote massa de tijdruimte dermate vervormt, dat voorwerpen binnen de waarnemingshorizon alleen naar het zwarte gat toe kunnen vallen - zie figuur.

Voor een waarnemer ver van een zwart gat vandaan lopen klokken dichter bij een zwart gat langzamer. Door deze gravitationele tijddilatatie lijkt een voorwerp dat naar een zwart gat valt steeds langzamer te bewegen. Ook andere processen lijken vertraagd: uitgezonden licht heeft een kleinere frequentie en vertoont naast verzwakking gravitationele roodverschuiving. Vlak voordat het voorwerp de waarnemingshorizon bereikt, wordt het licht zo zwak dat het van buiten de waarnemingshorizon niet meer kan worden gezien. Van binnen de waarnemingshorizon was en bleef de invallende lichtbron in principe altijd zichtbaar, omdat licht altijd van buiten de waarnemingshorizon naar binnen kan.

Maar voor een waarnemer die zelf invalt treden deze effecten niet op: zijn of haar klok blijft even snel gaan en na een eindige tijd wordt de waarnemingshorizon bereikt, hoewel de plaats ervan lokaal niet waar te nemen is. De waarnemer zou door de extreem grote gradiënt van het zwaartekrachtveld in de nabijheid van het zwarte gat echter wel worden "uitgerekt" tot een lange sliert ("spaghettificatie").

Als het zwarte gat niet draait, is de waarnemingshorizon bolvormig en ligt die op een afstand van de schwarzschildstraal van het centrum van het zwarte gat. Deze straal is evenredig met de massa M van het zwarte gat volgens de formule

$r_{\mathrm {SS} }={\frac {2GM}{c^{2}}}\approx 2,95\,{\frac {M}{M_{\mathrm {Zon} }}}~\mathrm {km}$

met $r_{\mathrm {SS} }$ de schwarzschildstraal, c de lichtsnelheid en G de gravitatieconstante en $M_{\mathrm {Zon} }$ de zonsmassa. Deze formule geldt voor zwarte gaten met elektrische lading Q en impulsmoment J nul (kan een factor 2 schelen voor andere zwarte gaten). Dus voor een stilstaand zwart gat met een zonsmassa ligt de waarnemingshorizon op een afstand van 2,95 km van het centrum. Draaiende zwarte gaten hebben een waarnemingshorizon die niet bolvormig is.

Uit het bovenstaande volgt dat de gemiddelde dichtheid binnen de schwarzschildstraal kleiner is naarmate de massa groter is; bij de grootste is deze dichtheid kleiner dan die van water.

De beschrijving van de waarnemingshorizon zoals de algemene relativiteitstheorie die geeft is een benadering, die mogelijk voor kwantumeffecten moet worden bijgesteld.

Temperatuur en entropie

Op grond van de tweede wet van de thermodynamica redeneerde de natuurkundige Jacob Bekenstein in 1970 dat zwarte gaten wel een zeer hoge mate van entropie moesten hebben of konden hebben, op basis van de gedachte dat de entropie in het gebied buiten de waarnemingshorizon afneemt wanneer er materie in het zwarte gat wordt gezogen. Dit idee werd echter verworpen op grond van de gedachte dat alles wat in een zwart gat valt voorgoed is verdwenen, en daarmee ook de entropie. In 1974 ontdekte Hawking echter – door het observeren van fotonenparen nabij de waarnemingshorizon, waarvan er één in het zwarte gat verdween terwijl de ander juist verder weg werd gestoten – dat zwarte gaten zelf wel degelijk straling (i.e. de hawkingstraling) uitzenden en bovendien een temperatuur hebben die boven het absolute nulpunt ligt. Dus moet er ook sprake zijn van entropie in zwarte gaten. Die entropie blijkt volgens berekeningen ontzettend hoog. Hawking kwam bovendien tot de conclusie dat naarmate een zwart gat minder massa heeft, de temperatuur hoger is en het meer straling uitzendt.

Vorming en evolutie

Ontstaan

Theoretisch zijn de volgende vier scenario's geopperd voor het ontstaan van zwarte gaten:

1. "Rechtstreeks, geïsoleerd": een zware ster stort in elkaar, bijna bolsymmetrisch, en brengt een neutronenster-kern voort die te zwaar is om zichzelf tegen de zwaartekracht in stand te houden;
2. "Onrechtstreeks, geïsoleerd": een ster met een witte dwerg-kern stort in elkaar en verliest door rotatie een deel van haar massa; de weggeslingerde fragmenten verliezen energie en draaimoment door het uitzenden van gravitatiegolven, en worden een voor een door het centrum ingevangen;
3. "Dicht opeengepakt": sterren in een dichtbevolkte cluster wisselen toevallig zwaartekracht-energie uit, waarbij sommige sterren uit de halo ontsnappen en de anderen dichter bij elkaar worden gedreven;
4. "Primordiaal": kleine dichtheidsverschillen in het jonge heelal creëren primordiale zwarte gaten, die geleidelijk zwaarder worden door het invangen van straling en materie.

De meeste zwarte gaten die we kennen, komen overeen met het eerste scenario; het zijn de overblijfselen van hypernova- of supernova-implosies. Als de kern van de imploderende ster meer dan ongeveer vijf keer zo zwaar is als de zon (de Oppenheimer-Volkofflimiet), implodeert de kern van de ster uiteindelijk tot een zwart gat, als gevolg van de enorme zwaartekracht die op de ster drukt en het uiteindelijk wint van de massa van de ster. Volgens de algemene relativiteitstheorie kan deze massa worden opgevat als geconcentreerd in een singulariteit. Dit kan een punt, een ring of een bol zijn - daarover zijn de geleerden het niet in alle gevallen eens.

De zeer zware zwarte gaten die in de centra van veel sterrenstelsels te vinden zijn en een massa van enkele miljoenen zonsmassa's hebben, zijn waarschijnlijk kort na de oerknal ontstaan. Inmiddels zijn er ook zwarte gaten bekend met een massa van enkele duizenden zonsmassa's, maar hoe die ontstaan zijn is nog niet duidelijk. Het is evenmin bekend wat er zich in en rond de singulariteit precies afspeelt, aangezien de algemene relativiteitstheorie op zulke kleine afstanden niet meer exact geldig is.

Volgens schattingen bevat ons eigen sterrenstelsel daarnaast enkele miljoenen zwarte gaten met elk ca. tien keer de massa van de zon, die zijn ontstaan uit zware sterren of uit botsingen tussen sterren. Wanneer deze zwarte gaten zich op een geïsoleerde plek bevinden, dat wil zeggen zonder andere sterren in de buurt, zijn ze veel moeilijker te ontdekken dan wanneer ze een dubbelstelsel vormen met een ster die eromheen draait; uit de baan die de ster dan aflegt kan de aanwezigheid van een donker en zwaarder object worden afgeleid.

Verdampen door hawkingstraling

De Engelse natuurkundige Stephen Hawking toonde in 1974 theoretisch aan dat zwarte gaten langzaam moeten verdampen. Volgens de onzekerheidswetten in de kwantumwereld ontstaan op de waarnemingshorizon voortdurend paren deeltjes en antideeltjes. Normaal heffen deze deeltjes zich bijna onmiddellijk weer op door onderlinge annihilatie zodat het energie-effect weer nul is. Bij een zwart gat gebeurt het echter soms dat een deeltje in het zwarte gat valt en dat het andere ontsnapt in de ruimte. Met andere woorden: er komt straling uit. Dit wordt ook wel 'hawkingstraling' genoemd. De energie hiervoor wordt onttrokken aan het zwarte gat. Dit wordt iets kleiner. Hoe kleiner het zwarte gat hoe sneller dit zal gaan. Na een tijd kan zo een zwart gat helemaal 'verdampen'. Aanvankelijk werd door sommige natuurkundigen gedacht dat de informatie die verloren ging doordat er bij het ontstaan van een zwart gat materie in viel, voorgoed verdwenen was.

Waarneming

De moeilijkheid met het waarnemen van zwarte gaten in het heelal is dat ze door hun sterke zwaartekrachtsveld geen licht kunnen uitstralen. Waarneming van deze hemellichamen is daardoor alleen indirect mogelijk, bijvoorbeeld door het gedrag van sterren in de onmiddellijke nabijheid te bestuderen.

Röntgenstraling

Gas van een nabije ster wordt naar het zwarte gat getrokken en gaat er een baan omheen beschrijven, daarbij een zogenaamde accretieschijf (aangroeischijf) vormend. Doordat de materie aan de binnenkant van de schijf sneller draait dan de lagen die er wat meer vandaan liggen, ontstaat er wrijving. Deze wrijving veroorzaakt röntgenstraling, die men kan waarnemen met een röntgentelescoop (zie röntgenastronomie). Het bestaan van andere zwarte gaten is afgeleid uit de bewegingen van één enkele ster of een dubbelster die om iets heen draaien wat niet zichtbaar is.

Sagittarius-A*

In het centrum van de Melkweg bevindt zich een superzwaarzwart zwart gat: Sagittarius A*. De massa hiervan kan bepaald worden door de banen van sterren te bestuderen die zich in de buurt van het centrum van de Melkweg bevinden, en blijkt 4,15 miljoen keer de massa van de Zon te bedragen. De schwarzschildradius voor een dergelijke massa bedraagt 0,08 astronomische eenheden. De maximale diameter van Sagittarius-A* die met de waarnemingen van nabijgelegen sterren in overeenstemming te brengen is, bedraagt 45 astronomische eenheden, zodat het voorlopig niet absoluut zeker is dat het hier om een zwart gat gaat.

Zwaartekrachtlens

Een zwaartekrachtlens doet zich voor als het licht van een verre heldere bron zoals een quasar door een zwaar hemellichaam wordt afgebogen. Dit heet in het Engels gravitational lensing. Het is een van de waarnemingen waarmee de voorspellingen van de algemene relativiteitstheorie getoetst kunnen worden. Volgens die theorie vervormt een massa de omliggende ruimte en moet licht deze kromming volgen wat een lens-effect geeft.

Een bron kan dankzij een zwaartekrachtlens voor de waarnemer soms verscheidene beelden voor de waarnemer opleveren. Als bron, zwaar hemellichaam en waarnemer op een lijn liggen, leidt de symmetrie tot een ringvormig beeld, een Einsteinring.

Omdat elk zwaar object zulke effecten kan geven, worden sommige lens-effecten aan de hemel waarschijnlijk niet door afzonderlijke zwarte gaten maar door verre sterrenstelsels veroorzaakt.

Zwaartekrachtgolven

Sterke veranderingen in gravitationele interactie, zoals bij een botsing tussen zwarte gaten, kunnen aanleiding geven tot gravitatiegolven en als dusdanig gedetecteerd worden met aangepaste instrumenten zoals de LIGO.

De totale energie die in de vorm van gravitatiegolven wordt uitgestraald wanneer een zwart gat met massa $M$ een object met massa $\mu$ invangt, bedraagt ongeveer $0{,}01\mu (\mu /M).$ De fractie van de massa van het invallende object die als energie wordt uitgezonden, is dus des te groter naarmate zijn massaverhouding tot het zwarte gat groter is.

Voorbeelden

De Chandra X-Ray Observatory heeft in september 1999 en oktober 2000 opnamen gemaakt van het centrum van het melkwegstelsel. Daar werd een enorm zwaar zwart gat waargenomen. Dit zwarte gat wordt in verband gebracht met de radiobron Sagittarius A^*. Met de Europese XMM-Newton satelliet worden regelmatig waarnemingen gedaan van zwarte gaten (officieel: mogelijke zwarte gaten, "black hole candidates").

In de Melkweg hebben we behalve Sagittarius A* in het centrum nog een aantal mogelijke zwarte gaten die dichterbij staan. Het gaat steeds om röntgendubbelsterren die via een accretieschijf gas aan hun begeleider onttrekken. Hun massa's liggen tussen de drie en twaalf zonsmassa's.

Naam	Massa in zonsmassa's M☉	Omlooptijd van begeleider (dagen)	Afstand tot de Aarde (lichtjaar)
2XMM J011028.1-460421 (HLX-1)	>500	-
MAXI J1409-619	onbekend	onbekend	-
4U 1543-475	8−10	1,1	~24000
A0620-00	9−13	0,33	~3500
Cygnus X-1	7-13	5,6	6000-8000
GRO J1655-40	6−6,5	2,8	5000−10000
GRO J0422+32	3−5	0,21	~8500
GS 2000+25	7−8	0,35	~8800
GX 339-4		1,75	~15000
GRS 1124-683	6,5−8,2	0,43	~17000
Sagittarius A*	3,7 miljoen	−	~26000
V404 Cygni	10−14	6,5	7800
XTE J1118+480	6,4−7,2	0,17	6200
XTE J1550-564	10−11	1,5	~17000
XTE J1819-254	10−18	2,8	< 25000

Verder lezen

• Begelman, M.C. & Rees, M.J.: Zwarte gaten in het heelal (populair-wetenschappelijk)
• Chandrasekhar, Subrahmanyan: The mathematical theory of black holes, Clarendon Press Oxford, 1984 (vakliteratuur)
• Misner, Charles W., Thorne, Kip S. & Wheeler, John Archibald: Gravitation, Freeman, San Francisco, 1970 en latere uitgaven (vakliteratuur)
• Novikov, I.: Zwarte gaten. De sleutel tot het ontstaan van het heelal, Contact, 1991 (populair-wetenschappelijk)
• Shapiro, Stuart L. & Teukolsky, Saul A.: Black holes, white dwarfs and neutron stars. The physics of compact objects, Wiley, New York 1983 (vakliteratuur)
• Thorne, Kip S.: Black holes and time warps. Einstein's outrageous legacy, Norton, New York 1994 en latere uitgaven (goed leesbaar, populair maar exact, aanbevolen)

Zie ook

• Grijs gat
• Naakte singulariteit
• Reissner-Nordströmmetriek
• Schwarzschildmetriek
• Subramanyan Chandrasekhar
• Susskind-Hawking battle
• Wit gat

Externe links

• Simulatie bij waarnemingen door Wilms en anderen met Europese XMM-Newton satelliet van MCG-6-30-15
• AstronomieAntwoorden (dr Louis Strous): Zwarte gaten
• Zwart gat neemt hapje ster (Kennislink artikel)
• Zwarte Gaten (UvA)
• Bewijs voor zwart gat in melkwegstelsel (Volkskrant artikel)
• Amusante en educatieve animaties over zwarte gaten

Noten

Referenties

Literatuur

• (en) Brian Greene The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory, 1999/2003.

Mediabestanden

Zie de categorie Black holes van Wikimedia Commons voor mediabestanden over dit onderwerp.

Stersoorten

Hoofdreeks: type O · type B · type A · type F · type G (gele dwerg) · dwergster · subdwerg · blauwe achterblijver · bruine dwerg · rode dwerg · oranje dwerg Reuzentak: blauwe reus · hyperreus · koolstofster · oranje reus · rode reus · S-type ster · subreus · superreus Post-hoofdreeks: witte dwerg · pulsar · magnetar · neutronenster · zwart gat Veranderlijke ster: Beta Cephei-veranderlijken · cataclysmisch variabele ster · cepheïde · Delta Scuti-veranderlijke · dubbelperiodische variabele · FU Orionis-ster · intermediaire polar · langzaam pulserende B-type ster · lichtsterke blauwe variabele · Mira-veranderlijke · OH/IR-ster · polar · pulserende witte dwerg · RR Lyrae-ster · T Tauri-ster · Thorne-Żytkow-object · vlamster · W Ursae Majoris-ster · Novae: dwergnova · hypernova · kilonova · micronova · rode nova · supernova · symbiotische nova Overige soorten: dubbelster · jong stellair object · protoster · röntgendubbelster · spectroscopische dubbelster · symbiotische dubbelster · vampierster · visuele dubbelster · Wolf-Rayetster (hypothetisch): blauwe dwerg · preonster · Q-ster · quarknova · quarkster · zwarte dwerg · donkere ster Gerelateerd: hoofdreeks · reuzentak · sterevolutie · stervorming

Astronomie

Disciplines: archeoastronomie · astrobiologie · astrochemie · astrodeeltjesfysica · astrofysica · gamma-astronomie · kosmologie · planetologie · infraroodastronomie · radioastronomie · röntgenastronomie · submillimeterastronomie Hemellichamen: komeet · manen (Maan) · meteoroïde · nevels en gaswolken · planeet (Aarde · dwergplaneet · exoplaneet) · planetoïde · ster (dubbelster · Zon · veranderlijke ster) · sterrenhoop · zwart gat Stelsels: heelal (Waarneembaar heelal) · supercluster (Laniakea · Virgosupercluster) · cluster (Lokale Groep) · sterrenstelsel (Melkweg) · planetenstelsel (zonnestelsel) Het einde: Big Crunch · Big Chill · Big Rip Overig: atmosfeer · heelal · messierobject · multiversum · oerknal · sterrenbeeld