Variëteit (wiskunde)

In de differentiaalmeetkunde en differentiaaltopologie, deelgebieden van de wiskunde, is een variëteit een topologische ruimte die lokaal, dat wil zeggen in een voldoend klein deel, op de euclidische ruimte, de ruimte die niet is gekromd, van een specifieke dimensie lijkt.[1] Een lijn, maar ook een cirkel zijn dus eendimensionale variëteiten, een achtvormige figuur zoals de lemniscaat van Bernoulli niet, want in het dubbelpunt, het punt waar de doorgaande lijn zichzelf snijdt, is er, hoe groot de schaal ook wordt gekozen, hoezeer men ook op dit punt inzoomt, geen overeenkomst met een eendimensionale euclidische ruimte. Een vlak en een boloppervlak zijn tweedimensionale variëteiten. Kijken we op aarde om ons heen, dan lijkt de aarde vlak en zullen we niet direct opmerken dat de aarde bol is. Er bestaan ook in alle hogere dimensies variëteiten, zoals de 3- en de 4-variëteit. Ieder punt van een -dimensionale variëteit heeft een omgeving die homeomorf is met een open deelverzameling van de -dimensionale ruimte .
Een variëteit beschrijft op een aantal verschillende manieren de gekromde ruimte. Alle definities delen het volgende idee:
- Een variëteit is een topologische ruimte die in voldoende kleine omgevingen van elk punt lijkt op de -dimensionale euclidische ruimte, maar die globaal een andere structuur kan hebben.
Hoewel variëteiten in de buurt van ieder punt in ieder geval lokaal op euclidische ruimten lijken, kan de globale structuur van een variëteit ingewikkelder zijn. Elk punt op het tweedimensionale boloppervlak wordt bijvoorbeeld omgeven door een cirkelvormig gebied, dat kan worden afgeplat tot een cirkelvormig gebied van het vlak, zoals in een geografische kaart. De structuur van het boloppervlak in zijn geheel, komt niet met die van een vlak overeen: in de taal van de topologie zijn zij niet homeomorf. De structuur van een variëteit is gecodeerd door een verzameling van kaarten die samen een atlas vormen, zoals een geografische atlas die uit kaarten van het oppervlak van de aarde bestaat. Het bol oppervlak is een tweedimensionale variëteit, omdat het oppervlak door een verzameling van tweedimensionale kaarten kan worden weergegeven.
Het "lokaal lijken op" kan verder gepreciseerd worden door bijectieve topologische afbeeldingen, dat worden kaarten genoemd, waarvan de samenstelling op de overlappingsgebieden van hun domeinen tot een bepaalde klasse moet behoren. Men spreekt naargelang de gekozen klasse van een topologische variëteit, of homeomorfisme, van een differentieerbare of gladde variëteit, of diffeomorfismen, of van een complexe variëteit, of complex differentieerbaar homeomorfisme. Sommige definities vereisen nog aanvullende structuur, bijvoorbeeld een riemann-variëteit is een gladde variëteit met een positief definiete kwadratische vorm.
Variëteiten staan centraal in veel delen van de meetkunde en de moderne wiskundige natuurkunde, omdat het met variëteiten mogelijk is gecompliceerde structuren uit te drukken en te begrijpen in termen van de relatief goed begrepen eigenschappen van eenvoudigere ruimten. Een variëteit is bijvoorbeeld typisch uitgerust met een differentieerbare structuur die het toelaat om te differentiëren en te integreren en een riemann-metriek, die waarmee afstanden en hoeken mee kunnen worden bepaald. Symplectische variëteiten fungeren binnen de klassieke mechanica als faseruimten in het hamiltonformalisme, terwijl vierdimensionale lorentz-variëteiten de ruimtetijd in de algemene relativiteitstheorie modelleren.
Het Engelse manifold, menigvuldigheid, wordt ook in Nederlandse teksten vaak als synoniem van variëteit gebruikt. Het Engels voor algebraïsche variëteit is algebraic variety.
Geschiedenis[bewerken | brontekst bewerken]
De studie van variëteiten combineert tal van belangrijke deelgebieden van de wiskunde: het veralgemeent concepten zoals krommen en oppervlakken alsmede ideeën uit de lineaire algebra en de topologie.
Voorbeelden[bewerken | brontekst bewerken]

Een oppervlak is een tweedimensionale variëteit, wat betekent dat de variëteit lokaal rond elk punt op het euclidische vlak lijkt. Het oppervlak van de wereldbol kan bijvoorbeeld worden beschreven door een verzameling kaarten, die samen een atlas van de wereld vormen. Hoewel geen van de afzonderlijke kaarten voldoende is om het gehele oppervlak van de wereld te bedekken, staat iedere plaats op de wereld op temminste één kaart.
Cirkel[bewerken | brontekst bewerken]
De cirkel is een eenvoudig, niet-triviaal voorbeeld van een topologische variëteit. Topologie zegt niets over kromming, dus wordt een klein stukje van een cirkel op precies dezelfde manier behandeld als een klein stukje van een lijn. Beschouw bijvoorbeeld de bovenste helft van de eenheidscirkel, beschreven door de vergelijking in het cartesisch coördinatenstelsel met , in figuur 1 aangegeven door de gele boog. Elk punt van deze halve cirkel wordt uniek beschreven door zijn -coördinaat. De projectie op de -as is een continue en inverteerbare, afbeelding van de open bovenste halve cirkel op het interval .
Zo'n functie wordt samen met het open gebied een kaart genoemd. Op gelijke wijze bestaan er kaarten voor de andere delen van de cirkel, die met blauw, rood en groen zijn aangegeven. Deze onderdelen bedekken samen de gehele cirkel en de vier kaarten vormen samen een atlas voor de cirkel.
De bovenste- en rechterkaart overlappen, hun doorsnede ligt in het kwart van de cirkel waar zowel de - als de -coördinaten positief zijn. De twee kaarten en beelden elk dit deel af op het interval .
Het is dus mogelijk de inverse van de bovenste kaart te gebruiken om vanuit een punt in de cirkel te bereiken en dan via de rechterkaart terug te gaan naar het interval. De functie die dit beschrijft heet transitie-afbeelding:

De bovengenoemde kaarten vormen niet de enige atlas. Een kaart hoeft niet per se een projectie te zijn en het aantal kaarten is een kwestie van keuze. Zo zijn er ook de kaarten:
en
Daarin is de helling van de lijn door het draaipunt en het punt op de cirkel. wordt op dezelfde manier ten opzichte van het draaipunt bepaald.
Deze twee kaarten vormen ook een atlas met een transitieafbeelding
Er is een punt waarin beide kaarten niet zijn gedefinieerd, namelijk hun draaipunt, zodat elke kaart alleen onvoldoende is om de hele cirkel te dekken. Het kan worden bewezen dat het niet mogelijk is de hele cirkel met een enkele kaart te beschrijven.
Boloppervlak[bewerken | brontekst bewerken]
Het boloppervlak is een voorbeeld van een oppervlak. De eenheidsbol, beschreven door de vergelijking:
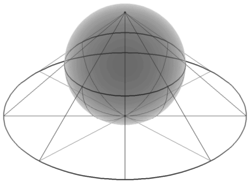
kan overdekt worden door een atlas met zes kaarten voor de halve sferen en , die elk op een open cirkelschijf geprojecteerd kunnen worden. Bijvoorbeeld kan de halve sfeer geprojecteerd worden op de schijf in het -vlak.
Net als bij de cirkel is het mogelijk de gehele sfeer op één punt na af te beelden op één kaart. In principe is dus een atlas met twee kaarten voldoende. Dit voorbeeld is historisch van belang, aangezien het aanleiding gaf tot de gebruikte terminologie. Het was namelijk duidelijk geworden dat de Aarde niet op één enkele kaart voorgesteld zou kunnen worden, zodat een atlas van kaarten nodig is.
Kaart[bewerken | brontekst bewerken]
De beschrijving van een variëteit gaat door middel van kaarten die gezamenlijk een atlas vormen waarmee de hele variëteit overdekt is. Een kaart brengt als het ware een deel van de variëteit in beeld door een zodanige correspondentie tussen dat deel en een euclidische ruimte dat de structuur behouden blijft.
In een topologische ruimte is een kaart een tweetal waarin een open deelverzameling van is, en een homeomorfisme van op zijn beeld in de euclidische ruimte . Het homeomorfisme wordt soms ook zelf als kaart aangeduid. Omdat aan een punt van de variëteit een rijtje in de toevoegt, wordt ook coördinatisering genoemd.
Transitieafbeeldingen[bewerken | brontekst bewerken]
Kaarten kunnen elkaar overlappen zodat een punt van een variëteit in meerdere kaarten wordt weergegeven. Als twee kaarten elkaar overlappen, geven van beide kaarten bepaalde gedeelten hetzelfde gebied van de variëteit weer, net zoals een kaart van Europa en een kaart van Azië beide Moskou kunnen bevatten. Tussen twee elkaar overlappende kaarten kan een overgangsfunctie worden gedefinieerd, de transitieafbeelding, die van het overlappende deel het verband tussen beide kaarten beschrijft. Van een open bal in gaat de transitieafbeelding via de inverse van de ene kaart naar de variëteit en vervolgens via de andere kaart terug naar een andere (of misschien dezelfde) open bal in . De transitieafbeelding, zoals de afbeelding in het bovenstaande voorbeeld van de cirkel, wordt ook coördinatentransformatie genoemd.
De transitieafbeeldingen tussen twee kaarten en zijn de functies
en
Compatibele kaarten[bewerken | brontekst bewerken]
Om ervoor te zorgen dat een bepaalde structuur door de verschillende kaarten goed beschreven wordt, zoekt men compatibele, vergelijkbare kaarten bij elkaar.
Twee kaarten en in een topologische variëteit heten -compatibel als de twee transitieafbeeldingen tussen de kaarten beide van dezelfde differentieerbaarheidsklasse zijn.
Atlas[bewerken | brontekst bewerken]
De beschrijving van de meeste variëteiten vereist meer dan één kaart. Een specifieke verzameling kaarten die een variëteit met de gewenste structuur beschijven, heet een atlas. Het gaat dan om kaarten die met elkaar compatibel zijn. Een atlas is niet uniek, omdat elke variëteit op meer dan één manier overdekt kan worden met behulp van verschillende combinaties van kaarten.
Een -atlas op een topologische ruimte is een familie paarsgewijze -compatibele kaarten waarvan de open verzamelingen de ruimte overdekken:
Compatibele atlassen[bewerken | brontekst bewerken]
Speciale gevallen van variëteiten stellen aanvullende eisen aan de transitieafbeeldingen van de atlassen. Zo zijn er gladde atlassen, waarvan de transitieafbeeldingen gladde functies, dus , zijn. Soms wordt minder geëist: van een -atlas zijn de transitieafbeeldingen van de klasse , dus keer continu differentieerbaar. Een -atlas heeft transitieafbeeldingen waarvan slechts geëist wordt dat ze continu zijn. Twee atlassen van dezelfde klasse heten compatibel als hun vereniging weer een atlas van dezelfde klasse is. Dit houdt in dat de transitieafbeeldingen tussen een kaart uit de ene atlas en een kaart uit de andere ook van de klasse van de atlassen zijn. Of anders gezegd, dat de kaarten in de ene atlas compatibel zijn met elke kaart in de andere.
Topologische variëteit[bewerken | brontekst bewerken]
Formele definitie[bewerken | brontekst bewerken]
Zij een positief natuurlijk getal. Een topologische variëteit van dimensie is een topologische ruimte die voldoet aan het scheidingsaxioma (Hausdorff) en aan het aftelbaarheidsaxioma , en waarin elk punt een omgeving heeft die homeomorf is met de euclidische ruimte
Topologische variëteiten worden bestudeerd in de tak van de wiskunde die algebraïsche topologie heet.
Voorbeelden[bewerken | brontekst bewerken]
Elke open deelverzameling van is op triviale wijze een topologische variëteit, want rond elk punt ligt een open bol binnen en -dimensionale open bollen zijn homeomorf (zelfs diffeomorf) met .
Een eenvoudige, maar niet triviale variëteit is de -sfeer, dit is de rand van de -dimensionale bol met middelpunt 0 en straal 1:
In elk punt bestaat er een uniek -dimensionaal raakhypervlak. Dit raakhypervlak is isometrisch (en dus zeker homeomorf en diffeomorf) met . De centrale projectie vanuit het tegenoverliggende punt op is een homeomorfisme (diffeomorfisme) tussen en .
Gladde variëteit[bewerken | brontekst bewerken]
Formele definitie[bewerken | brontekst bewerken]
Een gladde, differentieerbare variëteit of -variëteit is een topologische variëteit met een differentieerbare dat wil zeggen -atlas , waarvan dus de transitieafbeeldingen willekeurig vaak differentieerbaar zijn. Gladde variëteiten zijn het studieobject van de differentiaaltopologie.
Bovenstaande voorbeelden van topologische variëteiten kunnen zonder problemen worden geïnterpreteerd als gladde variëteiten. Iedere gladde variëteit beschikt over de belangrijke bijkomende structuur van een raakruimte in ieder punt en de bijhorende rakende bundel.
Exotische variëteiten[bewerken | brontekst bewerken]
De topologische structuur van een gladde variëteit legt de differentieerbare structuur niet op unieke wijze vast. Er bestaan gladde variëteiten die niet diffeomorf zijn met elkaar, maar waarvan de onderliggende topologische variëteiten wel homeomorf zijn. Dit is onder meer het geval met de topologische variëteit . Men spreekt van exotische differentiaalstructuren op om ze te onderscheiden van de triviale gladde structuur uit het voorbeeld hierboven.
Iets soortgelijks doet zich voor in de , de zevendimensionale sfeer.
Gladde afbeelding, diffeomorfisme[bewerken | brontekst bewerken]
Een continue afbeelding tussen twee gladde variëteiten van dimensie resp. heet glad als haar samenstelling met willekeurige kaarten (of hun inverse) op en , een onbeperkt differentieerbare afbeelding oplevert.
Een diffeomorfisme is een bijectie tussen gladde variëteiten die in beide richtingen een gladde afbeelding is. Dat deze laatste eis niet overbodig is, toont de afbeelding
Deze is een onbeperkt differentieerbaar homeomorfisme van de reële getallen naar zichzelf, maar de inverse is niet differentieerbaar in 0.
Doorsnede van gladde variëteiten[bewerken | brontekst bewerken]
De doorsnede van twee deelvariëteiten van een gladde variëteit is in het algemeen geen variëteit; dit is echter wel gegarandeerd als de twee deelvariëteiten elkaar dwars snijden.
Riemann-variëteit[bewerken | brontekst bewerken]
Een riemann-variëteit bestaat uit een gladde variëteit met een positief definiete kwadratische vorm in elke raakruimte (en zodanig dat de coëfficiënten van de kwadratische vorm in elk coördinatenstelsel onbeperkt differentieerbaar zijn).
De kwadratische vorm geeft betekenis aan het begrip "lengte" voor vectoren in de raakruimte, en (door integratie) voor krommen in de variëteit zelf.
Riemann-variëteiten zijn het studieobject van de moderne differentiaalmeetkunde.
Symplectische variëteit[bewerken | brontekst bewerken]
Een symplectische variëteit bestaat uit een gladde variëteit met een niet-ontaarde, antisymmetrische, gesloten bilineaire vorm. Symplectische variëteiten worden gebruikt om de faseruimte te modelleren in de hamiltoniaanse mechanica.
Symplectische variëteiten zijn het studieobject van de symplectische meetkunde.
Algebraïsche variëteit[bewerken | brontekst bewerken]
Een algebraïsche variëteit beantwoordt aan de filosofie uit de inleiding, op voorwaarde dat we de -dimensionale euclidische ruimte vervangen door , het -voudig cartesisch product van een algebraïsch gesloten lichaam (in België: veld) met zichzelf. De kaarten (afbeeldingen) moeten algebraïsch zijn, dat wil zeggen dat de coördinatentransformaties kunnen uitgedrukt worden als algebraïsche functies.
De algebraïsche meetkunde bestudeert algebraïsche variëteiten en aanverwante objecten.
Riemann-oppervlak[bewerken | brontekst bewerken]
Een riemann-oppervlak (niet te verwarren met een riemann-variëteit) is een tweedimensionale gladde variëteit waarvan de coördinatentransformaties kunnen worden opgevat als analytische functies (door de twee reële coördinaten te identificeren met de complexe getallen 1 en ).
Complexe variëteit[bewerken | brontekst bewerken]
Een complexe variëteit is een variëteit die lokaal op de complexe getallen in een of meer dimensies lijkt. Men spreekt van een analytische complexe variëteit als de coördinatentransformaties analytische functies zijn. Eendimensionale analytische complexe variëteiten heten riemann-oppervlakken.
Literatuur
|








































































