Geschiedenis van de wiskunde
| Wetenschapsgeschiedenis
|

|
|
|
|
Per tijdperk Exacte wetenschappen: Achtergrond |
|
Portaal |
De geschiedenis van de wiskunde bestudeert en beschrijft de oorsprong van ontdekkingen in de wiskunde en de ontwikkeling van methoden en notaties. De wiskunde is een formele wetenschap waarvan de gebruikelijke definitie is: het bestuderen van patronen en structuren in getallen, ruimte en vorm.
De wiskunde heeft een geschiedenis die teruggaat tot in de prehistorie. Kerfstokken uit de prehistorie wijzen erop dat men toen al telde.[1] Dit is de oorsprong van het begrip van de natuurlijke getallen. De Babyloniërs waren het eerste volk dat zich met wiskunde bezighield door praktische problemen op te lossen in de landbouw, handel, sterrenkunde en scheepvaart. Zij kenden reeds een soort stelling van Pythagoras[2] en waren in staat om vierkantsvergelijkingen op te lossen.[3]
In de loop van de geschiedenis hebben verschillende culturen en volkeren overeenkomstige ontdekkingen gedaan: de bepaling van pi, de wortel van 2, goniometrische functies en allerlei oplossingsmethoden voor wiskundige vergelijkingen.
Wiskunde in de prehistorie[bewerken | brontekst bewerken]
De mens moet begrip hebben gehad, hoe vaag dan ook, van aantal, afmeting en vorm. Paleontologen hebben in een grot in Zuid-Afrika ruim 70.000 jaar oude okerstenen gevonden met meetkundige figuren.[4] Ook vondsten van artefacten in Afrika en Frankrijk tonen aan dat de prehistorische mens besef had van tellen, aantallen aanduiden en vormen tekenen en herkennen.
In de loop der millennia nam het scheppend vermogen van de prehistorische mens toe. Een groot aantal kunstzinnige holschilderingen is bewaard gebleven. Die schilderingen van dieren en jagers, die voornamelijk in Spanje en Frankrijk te vinden zijn en die ongeveer 15.000 jaar oud zijn, hadden vermoedelijk een rituele betekenis en tonen aan dat er een uitstekend begrip was voor een tweedimensionale afbeelding van ruimtevormen.[5]
Er is bewijs gevonden dat de vrouwen in de prehistorie hun menstruatiecyclus bijhielden: 28 of 30 turfjes op een steen of in een bot, gevolgd door een onderscheidend merkteken.[6] Daarenboven kenden mogelijk herders en jager-verzamelaars het systeem van ‘geen’ (een primitieve nul), ‘één’, ‘een aantal’ en ‘veel’.[7] Ze gebruikten zogenaamde kerfstokken om aantallen bij te houden. Een van de oudste vondsten van kerfstokken is het Lebombo-beentje uit Swaziland, dat dateert van 35.000 v.Chr.[8]
Het Ishango-beentje[bewerken | brontekst bewerken]

Het Ishango-beentje[9][10] geldt als de oudste echte wiskundige vondst. Men schat de ouderdom op 22.000 jaar. Het beentje werd in 1960 ontdekt door Jean de Heinzelin de Braucourt, in dienst van het Koninklijk Belgisch Instituut voor Natuurwetenschappen. Het beentje werd genoemd naar de vindplaats Ishango, in Congo, op 15 kilometer van de evenaar, aan de oever van het Edwardmeer.
Op zijn sterfbed, in 1998, heeft De Heinzelin onthuld dat er nog een tweede staafje bestaat, ontdekt vlak bij het eerste staafje. Onderzoek door archeologen, wiskundigen en ingenieurs heeft aangetoond dat het telstokjes betreffen. Ze zijn waarschijnlijk opgesteld met bases 6 en 10, zoals gebruikelijk in verschillende Afrikaanse gebieden. De twee botjes zijn de oudste getuigenissen van logisch redeneren door de mens en de bakermat van de wiskunde.[11]
De voorkant van het beentje heeft drie inkervingen, dan zes. Vervolgens staan er vier inkervingen, dan acht. Dat is dus telkens maal twee. De som van alle inkervingen per kolom bedraagt respectievelijk 60, 48 en 60, allemaal veelvouden van zes. Dit kan er op wijzen dat men met een 6-delig of 60-delig talstelsel werkte[12] hoewel er ook kritiek is op die veronderstelling.[13]
Wiskunde in het oude Nabije Oosten ca. 3000 - 500 v.Chr.[bewerken | brontekst bewerken]
Babylonische wiskunde ca. 3000 - 1600 v.Chr.[bewerken | brontekst bewerken]

Babylonische wiskunde verwijst naar de wiskunde die bedreven werd door de volkeren uit Mesopotamië, het tegenwoordige Irak. Die periode begint met de Soemeriërs. Men noemt dit de Babylonische wiskunde vanwege de rol van Babylon als centrum van studie en wetenschappelijk onderzoek. Dit hield op met de hellenistische periode.
In tegenstelling tot de Egyptische wiskunde, die wij al lang kenden door de hiërogliefen, kennen wij de Babylonische wiskunde van de meer dan 400 kleitabletten, die werden opgegraven vanaf de jaren 50 van de 19e eeuw. Die kleitabletten bevatten tekens in spijkerschrift, die in de vochtige klei werden gekrast en dan te drogen gelegd in de zon of in een oven.
Het vroegste bewijsmateriaal van geschreven wiskunde, gaat terug naar de oude Sumeriërs. Zij ontwikkelden een complex systeem van metrologie vanaf 3000 v.Chr.[14][15] Vanaf ongeveer 2500 v.Chr. schreven de Sumeriërs tafels van vermenigvuldiging op kleitabletten[16] en behandelden geometrische oefeningen en wiskundige problemen, zoals de deling. De vroegste sporen van de Babylonische cijfers dateren ook van deze periode.[17]
De meeste ontdekte kleitabletten dateren van 1800 tot 1600 v.Chr., en gaan over onderwerpen als breuken, algebra, vierkantsvergelijkingen en de berekening van pythagorese drietallen, bijvoorbeeld Plimpton 322.[18] De meeste kleitabletten bevatten tafels van vermenigvuldiging, tabellen met goniometrische getallen en methodes om vierkantsvergelijkingen op te lossen. Het Babylonisch tablet YBC 7289 uit 1900 - 1600 v.Chr. geeft een benadering voor tot op vijf cijfers na de komma nauwkeurig:
Babyloniërs gebruikten een 60-tallig of sexagesimaal talstelsel. Daarvan stammen nu nog 60 seconden in een minuut, 60 minuten in een uur, 24 uur in een dag en 360 graden in een cirkel. Ook in de taal is deze onderverdeling nog steeds te merken: een dozijn is 12 en een gros is 144, allemaal getallen die deelbaar zijn door 6 of 12. Zestig is wellicht gekozen omdat het twaalf delers bezit: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 en 60.
Egyptische wiskunde ca. 2700 v.Chr. - 500 v.Chr.[bewerken | brontekst bewerken]
De Egyptische wiskunde verwijst naar wiskunde die in de Egyptische taal wordt geschreven. Vanaf de hellenistische periode verving het Grieks het Egyptisch als geschreven taal van de Egyptische geleerden, en vanaf dat moment voegde de Egyptische wiskunde zich bij de Griekse en Babylonische wiskunde om tot de hellenistische wiskunde te leiden. De Egyptische wiskundige studie ging later over in de Arabische wiskunde, en tevens werd het Arabisch de geschreven taal van de Egyptische geleerden.[20]
De Papyrus van Moskou[bewerken | brontekst bewerken]

De oudste tot dusver ontdekte wiskundige tekst is de Papyrus van Moskou, een Egyptische Middenrijks tekst op papyrus[21] gedateerd op 2000 - 1800 v.Chr. De papyrus bevat wat vandaag "woordproblemen" of "verhaalproblemen" worden genoemd, blijkbaar als vermaak bedoeld. Zo bepaalt een Egyptisch probleem het volume van een afgeknotte piramide:
Als je wordt gezegd: een afgeknotte piramide met een verticale hoogte van 6, een basis van 4 en de basis op de top van 2, dan moet je 4 in het kwadraat nemen, dat is 16. Vervolgens neem je 2 maal 4, dat is 8. Dan neem je het kwadraat van 2, dat geeft 4. Vervolgens moet je de 16, de 8 en de 4 bij elkaar optellen, dat resulteert in 28. Van de verticale hoogte (6) moet je één derde nemen, dat geeft 2. Als laatste stap neem je 28 keer 2, dat geeft 56. Ziehier het resultaat.
Dit klopt, want de formule voor het volume van de afgeknotte piramide luidt:
waarin de loodrechte hoogte voorstelt van het ondervlak tot het bovenvlak, en zijn de oppervlakten van onder- en bovenvlak.
De Rhind-papyrus[bewerken | brontekst bewerken]

De Rhind-papyrus[22] (ca. 1650 v.Chr.) is een andere belangrijke Egyptische wiskundige tekst, genoemd naar de Schotse egyptoloog Alexander Henry Rhind, die de papyrus in 1858 in Luxor kocht en later aan het British Museum schonk. Het is een soort vragen- en instructiehandboek in rekenkunde en meetkunde, waarin 87 vraagstukken staan met de bijbehorende uitwerkingen.[23] Naast het geven van formules en methodes voor vermenigvuldiging, deling en het werken met breuken, bevat hij ook bewijsmateriaal van andere wiskundige kennis, met inbegrip van samengestelde getallen, de priemgetallen, het rekenkundig gemiddelde, het meetkundig gemiddelde en het harmonisch gemiddelde.[24] Hij bevat bovendien een simpele uitleg voor de zeef van Eratosthenes, evenals voor de theorie van de perfecte getallen, in het bijzonder die van het getal 6. Hij toont ook hoe men een lineaire vergelijking moet oplossen, evenals het oplossen en begrijpen van rekenkundige en meetkundige rijen.[25]
Ook suggereren drie meetkundige elementen in de Rhind-papyrus dat de Egyptenaren zich bezighielden met de analytische meetkunde:
- Het getal benaderen tot op 3,16045,[26] met een onnauwkeurigheid van minder dan 1 procent.
- Een vroege poging tot het oplossen van het probleem van de kwadratuur van de cirkel.[27]
- Het vroegste gebruik van een soort cotangens.[28]
De Papyrus van Berlijn[bewerken | brontekst bewerken]
De Papyrus van Berlijn is een Egyptisch geschreven papyrustekst over wiskunde uit het Middenrijk (ca. 1300 v.Chr.). Hij werd gevonden in de dodenstad Saqqara in het begin van de 19e eeuw. Hij toont aan dat de oude Egyptenaren een vierkantsvergelijking algebraïsch konden oplossen en dat ze een primitieve vorm van de stelling van Pythagoras toepasten om een landbouwkundig vraagstuk op de lossen.[25]
Toch bevat hij niet enkel wiskundige teksten, maar ook een soort procedure om te bepalen of een vrouw zwanger was. Het was dus ook een soort medische papyrus.
Oude Chinese wiskunde ca. 1500 - 500 v.Chr.[bewerken | brontekst bewerken]

De eerste tekenen van wiskunde in China vinden we rond 1500 v.Chr.[29] Toen raakten voor het eerst Chinese cijfers in gebruik.
Men gebruikte in China numerieke notaties, maakte rekenkundige berekeningen en telde met behulp van telstaafjes. Het stelsel heeft als grondtal 10 (decimaal talstelsel). Er werden karakters gebruikt voor de cijfers 1, 2, 3, ..., alsmede voor 10, 100, 1000, ... Eigenaardig voor de Chinese getalnotatie was dat men voor nul een spatie gebruikte.
Diverse rekenkundige berekeningen werden uitgevoerd met kleine telstokjes uit bamboe. Optellen en aftrekken vond plaats met behulp van telstokjes en voor vermenigvuldigen gebruikt met tabellen tot 9 maal 9. Later ging men (en ook nu nog) andere symbolen voor de cijfers 0, 1, 10 gebruiken in China.
Oude Indiase wiskunde ca. 900 v.Chr. - 200 n.Chr.[bewerken | brontekst bewerken]
De wiskunde in India begon al in de vroege ijzertijd, met de Shatapatha-Brahmana (ca. 9e eeuw v.Chr.), een tekst die de waarde van tot op 2 decimalen benadert.
De Sulba Sutras (ca. 800-500 v.Chr.) waren teksten die vooral meetkundige onderwerpen behandelden en die gebruikmaakten van irrationale getallen, priemgetallen, de kruislings vermenigvuldigen en derdemachtswortels. De tekst benaderde de waarde van tot op 5 decimalen, gaf een uitleg voor het probleem van de kwadratuur van de cirkel, loste lineaire en vierkantsvergelijkingen op, ontwikkelde een methode voor pythagorese drietallen en gaf een bewijs voor de stelling van Pythagoras.
Baudhayana (ca. 8e eeuw v.Chr.) stelde de Baudhayana Sulba Sutra samen, waarin hij een aantal voorbeelden van eenvoudige pythagorese drietallen geeft, zoals (3,4,5), (5,12,13), (8,15,17), (7,24,25) en (12,35,37), alsook een verklaring voor de stelling van Pythagoras voor de zijden van een vierkant:
Wanneer men een koord spant dwars over de diagonaal van een vierkant met een welbepaalde oppervlakte en daar een vierkant mee vormt, dan bekomt men een vierkant met een oppervlakte die 2 maal groter is dan de oppervlakte van het oorspronkelijke vierkant
Baudhayana geeft ook een formule voor de vierkantswortel uit twee:[30]
Deze formule is correct tot op 5 cijfers na de komma (de echte waarde bedraagt 1,414213562... ).
Pāṇini, een Sanskrietgeleerde en taalkundige uit 5e eeuw v.Chr., formuleerde de grammaticale regels voor het Sanskriet in zijn magnum opus Aṣṭādhyāyī. Zijn handschrift leek op de moderne wiskundige notatie, en tevens hanteerde hij transformaties en recursiviteit met dermate verfijning, dat het de capaciteit van een turingmachine evenaarde.
Pingala, een Indiase schrijver uit de 3e-1e eeuw v.Chr., hanteerde in zijn traktaat over metriek een systeem dat grotendeels overeenkomt met het huidige binaire talstelsel. Pingala's werk bevat ook een aantal basisideeën over de rij van Fibonacci (Sanskriet: mātrāmeru).

Het Brāhmīmanuschrift werd het laatst mogelijk rond de 4e eeuw v.Chr. ontwikkeld, maar er zijn recente archeologische onderzoeken, die aantonen dat het misschien nog ouder is (ca. 600 v.Chr.). De Brāhmīgetallen dateren van rond de 3e eeuw v.Chr.
Tussen 400 v.Chr. en 200 n.Chr. bestudeerden Indiase wiskundigen, met name de volgelingen van het jaïnisme, als eersten de transfiniete getallen,[31] verzamelingenleer[31] en de logaritmen.[31] Ze ontwikkelende ook fundamentele wetten van de indexen, vierkantsvergelijkingen, vierdegraadsvergelijkingen, oneindige machtsverheffingen, combinatoriek en rijen.[31] Ze bedachten ook een woord om niets (dus het getal nul) aan te duiden: shunya, wat in het Sanskriet leegte of leemte betekent. Dat woord evolueerde: in het Arabisch werd het ṣifr (betekenis: nul, maar ook het woord cijfer stamt ervan) en later ṣafira, in het Italiaans zefiro en dan in het Frans en Engels zero.[32]
Het Bakhshalimanuscript (tussen 200 v.Chr. en 200 n.Chr.) bevat oplossingen voor lineaire vergelijkingen met maximaal 5 onbekenden, de oplossing van vierkantsvergelijkingen, rekenkundige en meetkundige vooruitgangen, stelsels en het gebruik van de nul en negatieve getallen.[33]
Griekse wiskunde ca. 550 v.Chr. - 300 n.Chr.[bewerken | brontekst bewerken]

Geografie en tijdsindeling[bewerken | brontekst bewerken]
De klassieke Griekse wiskunde refereert aan de periode waarin men de wiskunde bestudeerde voor de hellenistische periode. De Griekse wiskunde was verspreid over de Griekse poleis en in Klein-Azië, Libië en Sicilië.
Griekse wiskunde, die vanaf de hellenistische periode werd bestudeerd (vanaf 323 v.Chr.), verwijst naar de wiskunde die in het Grieks is opgesteld door Griekse wiskundigen uit het gehele hellenistische gebied, dat reikte van het Middellandse Zeegebied tot het Verre Oosten, ongeveer het rijk van Alexander de Grote. Vanaf dat moment voegde de Griekse wiskunde zich samen met de Babylonische en Egyptische wiskunde, om zo de hellenistische wiskunde te laten ontstaan. Deze fase noemt men de Pan-Helleense fase. Het epicentrum van de Griekse wiskunde lag op dat ogenblik niet meer in Athene, maar in Alexandrië (huidig Egypte). Vele geleerden vanuit de gehele hellenistische wereld (over het algemeen Griekse en Egyptische, maar ook heel wat Perzische, Arabische, Joodse, Fenicische en Indiase geleerden) werden hierdoor aangetrokken.
Het grootste deel van de wiskundige teksten en manuscripten in het Grieks werden gevonden in Griekenland, Egypte, Klein-Azië, Mesopotamië en Sicilië.
Oorsprong en invloeden[bewerken | brontekst bewerken]
De Griekse wiskunde vond haar oorsprong rond de 7e eeuw v.Chr., maar er is weinig bronnenmateriaal uit die tijd. De Grieken werden wellicht geïnspireerd door de oudere methodes van Babyloniërs en Egyptenaren, maar er zijn ook aanwijzingen voor Fenicische en zelfs Indiase invloeden.
De echte Griekse wiskunde begon rond 550 v.Chr., toen Thales van Milete en Pythagoras kennis van Babylonische en Egyptische wiskunde naar Griekenland brachten. Thales gebruikte meetkunde om praktische problemen op te lossen, zoals het berekenen van de hoogte van een piramide en de afstand van schepen tot de kust. Pythagoras bewees voor het eerste de stelling van Pythagoras en construeerde op algebraïsch wijze de pythagorese drietallen.
Verwezenlijkingen[bewerken | brontekst bewerken]

De Griekse wiskunde vormt een belangrijke periode in de geschiedenis van wiskunde, fundamenteel door de geavanceerde meetkunde en het idee van het formeel bewijs. De Griekse wiskunde droeg ook bij tot ideeën over de getaltheorie, wiskundige analyse, toegepaste wiskunde, en af en toe kwam men zelfs dicht bij de integraalrekening.
Bekende Griekse wiskundigen als Pythagoras, een mystiek persoon van het eiland Samos en geassocieerd met de mystiek van de getallen en de numerologie, en Euclides, die voor zijn Elementen, een werk over meetkunde, doorheen alle eeuwen bekendheid bleef verwerven, werden vaak becommentarieerd en bestudeerd door wiskundigen van andere afkomst.
Diophantus schreef zijn beroemd werk Arithmetika en bestudeerde diofantische vergelijkingen.
Het kenmerkendste product van de Griekse wiskunde is de theorie van kegelsneden, die Apollonius van Perga beschreef in zijn Konika van 225 voor Christus. De aangewende methodes maakten geen expliciet gebruik van algebra of goniometrie.
Eratosthenes, een Grieks bibliothecaris in de bibliotheek van Alexandrië, ontwikkelde een eenvoudig algoritme om de priemgetallen te vinden: de zeef van Eratosthenes. Hij berekende ook de omtrek van de Aarde op zo'n 15 procent groter (250.000 stadiën[34] of ongeveer 46.000 kilometer) dan de echte waarde van 40.074 kilometer.
Plato beschreef in zijn werk Timaeus de 5 mogelijke regelmatige driedimensionale lichamen, de regelmatige veelvlakken of Platonische lichamen.
De gulden snede[bewerken | brontekst bewerken]

In de 5e eeuw v.Chr. werd de gulden snede ontdekt. Phidias, een Grieks beeldhouwer, is mogelijk de eerste die de gulden snede heeft toegepast in zijn beeldhouwwerken in het Parthenon. Het symbool voor de gulden snede is de Griekse letter phi (φ), naar de eerste letter van de naam Phidias (Φειδίας).
Euclides gaf in zijn Elementen de eerst bekende definitie van de gulden snede, die hij aanduidde als "extreme en gemiddelde verhouding" (Grieks: ακρος και μεσος λογος; akros kai mesos logos). De Italiaan Luca Pacioli ontrukte die in zijn De Divina Proportione (over de goddelijke verhouding) van 1509 aan de vergetelheid.
Bloeiperiode[bewerken | brontekst bewerken]

De hellenistische wiskunde kende van ca. 420 tot 150 v.Chr. een periode van grote bloei. De wiskundige ontwikkelingen vonden plaats in de Griekstalige centra zoals Egypte en Sicilië, en met een hoge waardering voor het intellectuele en culturele statuut van de wiskunde, zoals in de school van Plato. De zandrekenaar (Grieks: Ψαμμίτης, Psammitès), een boek van Archimedes, een getaltheoretisch en astronomisch werk van grote originaliteit, schat de diameter van het heelal op ongeveer twee lichtjaar,[35] een volume waar ongeveer 1063 zandkorrels in passen. Archimedes toonde aan dat een bol 2/3 van de oppervlakte en het volume van een cilinder met zelfde straal en hoogte bezit en liet dit op zijn graf beitelen. Het Archimedespalimpsest, een hergebruikt perkament uit de 13e eeuw (april 1229)[36] waarin een tekst van Archimedes is verborgen, is bewaard gebleven. Het document is van buitengewoon belang voor de geschiedenis van de wetenschap. Het werk bevat de enige overgeleverde Griekse versie van Drijvende lichamen en de enige afschriften van de Methode van mechanische stellingen en Stomachion.
Het werk van geleerden als Hipparchus en Posidonius lag mogelijk aan de basis van het mechanisme van Antikythera.
De Almagest (oorspronkelijke titel Ἡ μαθηματικὴ σύνταξις, De mathematische ordening) - een verhandeling over de schijnbare bewegingen van de sterren en de planeten - van Claudius Ptolemaeus, die op meerdere terreinen actief was, zou tot aan Copernicus grote invloed uitoefenen.
Overlevering[bewerken | brontekst bewerken]
Hoewel de vroegste Griekse teksten over wiskunde die gevonden zijn, na de hellenistische periode zijn geschreven, worden veel van deze werken beschouwd als kopieën van werken die tijdens de hellenistische periode zijn geschreven. Toch is de datering van Griekse teksten veel eenvoudiger dan de datering van vroegere wiskundige documenten, omdat er een groot aantal chronologische teksten zijn (waaronder jaarverslagen), die elkaar soms overlappen in tijd. Daardoor is het gemakkelijk om een chronologie van de Griekse wiskunde op te stellen en zo een beeld te krijgen van de toenmalige wiskunde. Maar toch tasten we voor vele data nog in het duister, al is de twijfel eerder een kwestie van decennia dan van eeuwen. Zo bewees Pappos van Alexandrië de stelling van Pappos.
Tijdens de middeleeuwen leidde Europa veel van zijn kennis van Griekse wiskunde af via de islamitische wiskunde. De teksten over Griekse wiskunde werden grotendeels bewaard en gekopieerd door Arabische en Perzische geleerden. Ze werden ginds lange tijd bewaard en bestudeerd (door onder andere Mohammed ibn Moesa al-Chwarizmi,[37] Qutb al-Din al-Shirazi en Abu Ali al-Hasan ibn al-Haytham), waarna ze in Europa werden geïntroduceerd.
Romeinse wiskunde[bewerken | brontekst bewerken]


Op wiskundig vlak hebben de Romeinen niet bepaald een voortrekkersrol gespeeld. De Romeinse cijfers zijn waarschijnlijk ontstaan als een telsysteem voor herders, die op een kerfstok bijhielden of ze wel met al hun schapen terug thuis waren gekomen. Later evolueerden de kerfstreepjes tot letters, die uit het Romeinse alfabet werden overgenomen. Maar het bleef een primitief systeem. Dit staat in schril contrast met de hoge vorm van beschaving en de daarbij horende technische vernieuwingen in het Romeinse Rijk.
Het maken van de eenvoudige berekeningen als optellen, aftrekken, vermenigvuldigingen en delingen, was met Romeinse getallen een grote opgave. Het talstelsel werd alleen gebruikt voor notaties, en berekeningen gebeurden met een abacus of rekentafel. Nochtans bleef het systeem in Europa nog tot in de middeleeuwen algemeen in zwang.
Het moeilijke rekenwerk werd veroorzaakt door het feit dat het Romeinse talstelsel addititief was: de waarde van het voorgestelde getal wordt bepaald door het totaal van de samentellende symbolen. Bijna per definitie geven ze dus ook alleen maar gehele, positieve waarden weer.
Klassieke Chinese wiskunde ca. 500 v.Chr. - 1300 n.Chr.[bewerken | brontekst bewerken]
Oudste overblijfselen[bewerken | brontekst bewerken]
Van de westelijke Zhou-dynastie (vanaf 1049-1046 v.Chr.) is het oudste wiskundige werk dat is overgebleven het Boek der Veranderingen of Yijing (易經), dat gebruikmaakt van de 8 binaire trigrammen en de 64 binaire hexagrammen, voor filosofische, wiskundige en mystieke doeleinden. In het boek worden betekenissen van de 64 hexagrammen omschreven. Deze hexagrammen stellen beelden voor, die van onder naar boven worden opgebouwd. De hexagrammen ontstaan door bijvoorbeeld het zes maal achtereenvolgens opgooien van drie munten. Een oneven aantal "koppen" (Chinese munten hadden in het algemeen slechts aan één zijde tekst; dat is de kopzijde) levert in het heden een Yang-lijn op; een even aantal een Yin-lijn. Drie gelijke zijden vormen een "sterke" lijn.
Volgens de oorspronkelijke manier van het bekomen van de hexagrammen werd gebruikgemaakt van 50 stengels van het duizendblad. Via herhaaldelijke ordening van de stengels bekwam men Yin-lijnen of Yang-lijnen, die elk veranderend of niet veranderend konden zijn. Sterke lijnen geven een aankomende verandering aan. Elk beeld kan op zes verschillende manieren veranderen. Deze hexagrammen worden op hun beurt weer ontleed in diverse trigrammen. Elk trigram bestaat uit een combinatie van drie horizontale, boven elkaar geplaatste lijnen. De lijnen kunnen Yin of Yang zijn. Een ononderbroken lijn is een (mannelijke) Yang-lijn (陽), een in het midden onderbroken lijn een (vrouwelijke) Yin-lijn (陰).
Het oudste bestaande werk aangaande meetkunde uit China komt uit de Mohistische canon of Mo Jing (墨家) (ca. 330 v.Chr.), die door de aanhangers van de Chinese filosoof Mozi werd gebundeld (tussen ca. 470 en 390 v.Chr.). De Mo Jing beschreef diverse aspecten van wetenschappelijke domeinen, die gelinkt worden aan de huidige natuurkunde, en verstrekte een kleine bron aan informatie over wiskunde.
Grote boekverbranding[bewerken | brontekst bewerken]
In China beval keizer Qin Shi Huangdi (Huang-Ti Shi) in 212 v.Chr. dat alle boeken buiten Qin moesten worden verbrand. Hoewel dit bevel niet overal werd uitgevoerd, is er weinig bekend over de klassieke Chinese wiskunde uit die tijd.
Na de boekverbrandingen produceerde de Han-dynastie (202 v.Chr. - 220 n.Chr.) werken over wiskunde, die schrijven over verloren manuscripten. Het belangrijkste hiervan is De negen hoofdstukken van de wiskundige kunst (九章算術). Het boek is ouder dan het jaar 179, want uit dat jaar stamt een exemplaar met alle hoofdstukken.
Het bestaat uit 246 woordproblemen, onder andere over landbouw, zaken, het gebruik van geometrische figuren voor de bouw van pagodes, en het omvat informatie over rechthoekige driehoeken en het getal . Het maakte eveneens gebruik van het principe van Bonaventura Cavalieri over volume, meer dan 1000 jaar voor die het in het westen zou invoeren. Het bevatte een bewijs voor de stelling van Pythagoras en formules voor de Gauss-eliminatie. Het werk werd becommentarieerd door Liu Hui in het midden van de 3e eeuw.
Bovendien bevatten de werken van de astronoom Han en de uitvinder Zhang Heng (78 - 139 n.Chr.) een andere formule voor , die hij gebruikte om het volume van een bol te berekenen.
Latere ontwikkelingen[bewerken | brontekst bewerken]
Er was ook het geschreven werk van de wiskundige en muziektheoreticus Jing Fang (78 - 37 v.Chr.). Door het gebruik van de pythagoreïsche komma, ontdekte Jing dat 53 kwinten ongeveer 31 octaven benadert. Dit zou later leiden tot de ontdekking van gelijkzwevende stemming. Het werd lange tijd niet berekend, tot de Pruisische wiskundige Nikolaus Mercator dit in de 17e eeuw opnieuw deed.
De Chinezen maakten ook gebruik van een aantal complexe diagrammen, die bekendstaan als het magisch vierkant en de magische cirkel. Het systeem werd reeds beschreven in oude tijden, maar werd pas geperfectioneerd door de wiskundige Yang Hui (1238–1298).
In de 4e eeuw beschreef het rekenkundig handboek van Meester Sun, Sunzi Suanjing (孫子算經) de Chinese reststelling om de grootte van het leger te tellen.
Wiskunde bij de Maya's ca. 100 - 900[bewerken | brontekst bewerken]

De Maya's beoefenden in zekere zin de wiskunde door hun bijzonder nauwkeurige astronomische waarnemingen en de ontwikkeling van een nauwkeurige en ingewikkelde kalender. Hun tabellen voor de bewegingen van de Maan en de planeten zijn even goed of zelfs beter dan die van andere beschavingen die met het blote oog de hemel bestudeerden. De berekening van het zonnejaar is zelfs iets nauwkeuriger dan de waarde die als basis voor de gregoriaanse kalender gebruikt is.
Getallen[bewerken | brontekst bewerken]
De Maya's en hun Olmeekse voorgangers hadden geheel onafhankelijk het begrip 'nul' (dat in de Oude Wereld pas laat werd ingevoerd) ontdekt, dat ze xix im noemden. Ze gebruiken het getal 20 als grondtal van hun talstelsel, omdat ze zich baseerden op de 10 vingers van de handen en de 10 tenen van de voeten.[38] In het decimale systeem, waarmee in de Westerse wereld wordt gewerkt, kunnen getallen bestaan uit cijfers tussen 0 en 9. Bij de Maya's bestonden getallen uit cijfers tussen 0 en 19, waardoor het gemakkelijker was om grotere getallen weer te geven. Inscripties vermelden soms getallen die tot in de honderden miljoenen reiken.
Overgebleven manuscripten[bewerken | brontekst bewerken]
De Dresdener codex is een oud Maya-handschrift uit de 11e eeuw of 12e eeuw van de Maya's uit Chichén Itzá. Het is een van de vier overgebleven Maya-handschriften. Daaruit blijkt dat de Maya's rond 1100 al maansverduisteringen konden voorspellen en de banen van Mars en Venus konden beschrijven.[39] De codex bestaat uit 39 bladzijden, elk 20,5 cm hoog en 10 cm breed en wordt in Dresden bewaard.[40] De andere drie worden in Parijs, Madrid en Mexico bewaard.
Klassieke Indiase wiskunde ca. 400 - 1600[bewerken | brontekst bewerken]

Rond het jaar 400 introduceerde het Indiase traktaat Surya Siddhanta (Hindi: सूर्य सिद्धांत) de sinus, de cosinus en daarvan de omgekeerden in de Indiase wiskunde, waarmee het tot bloei kwam. Deze functies waren erg belangrijk, omdat ze ook op andere vlakken werden gebruikt, zoals de beweging van de sterren en de scheepsnavigatie. De kosmologische tijdscycli die in de tekst worden verduidelijkt, werden gekopieerd van een ouder werk, en leidden tot de berekening van een siderisch jaar van 365,2563627 dagen. Dit is slechts 1,4 seconden langer dan de moderne berekening van 365,25636305 dagen. Dit traktaat werd in de middeleeuwen vertaald naar het Arabisch en het Latijn.
Aryabhata introduceerde in 499 een nieuwe functie: de sinus versus. Hij maakte ook een eerste goniometrische tabel van de sinus, ontwikkelde technieken en algoritme aangaande algebra, infinitesimalen, differentiaalvergelijkingen en hij bekwam een hele reeks oplossingen voor de lineaire vergelijkingen. Daarbij maakte hij gebruik van een methode die equivalent is aan de moderne methode, samen met accurate astronomische berekeningen die gebaseerd waren op het heliocentrische systeem van zwaartekracht. Deze Indiase wiskundige schreef in 499 zijn magnum opus Aryabhatiya, dat reeds in de 8e eeuw naar het Arabisch werd vertaald en in de 13e eeuw naar het Latijn. Hij berekende ook nog eens de waarde van tot op 4 cijfers na de komma: 3,1416. Later in de 14e eeuw berekende Madhava de waarde tot op 11 decimalen: 3,14159265359.
In de 7e eeuw bedacht Brahmagupta de stelling van Brahmagupta, de identiteit van Brahmagupta en de formule van Brahmagupta. Voor de eerste keer in de geschiedenis legde hij het gebruik van nul zeer duidelijk uit in zijn werk Brahmasphuta-siddhanta uit 628. Hij gaf ook duidelijke uitleg over de Arabisch-Indische cijfers. Van de vertaling van deze tekst over wiskunde was het dat de Arabische wiskundigen rond 770 werden geïntroduceerd in dit telsysteem, dat zij overnamen. De Arabische geleerden namen dit telsysteem mee en gebruikten het tot de 12e eeuw. Toen werd het ook in Europa overgenomen. Op die manier hebben de Arabisch-Indische cijfers vrijwel alle andere telsystemen in de wereld verdreven.
Klassieke Arabische wiskunde ca. 800 - 1500[bewerken | brontekst bewerken]
Arabische expansie[bewerken | brontekst bewerken]
Het Arabische Rijk breidde zich in de 8e en 9e eeuw uit over het Midden-Oosten, Centraal-Azië, Noord-Afrika, het Iberisch schiereiland en enkele delen van India. Mede door deze geografische expansie werd de invloed van de Arabische wiskundigen in die tijd veel groter. Arabische geleerden uit die tijd namen ook werkmethodes van andere volkeren over en begonnen deze uit te breiden, waardoor ook de Arabieren grote vooruitgang maakten binnen alle wetenschappen, maar vooral de wiskunde. Hoewel de meeste islamitische teksten over wiskunde geschreven waren in het Arabisch, waren de teksten zelf niet allemaal geschreven door Arabieren. Zoals het Grieks in de hellenistische wereld werd gebruikt als een soort statussymbool, werd het Arabisch door niet-Arabische geleerden gebruikt als hun geschreven taal. Dit is niet verwonderlijk, aangezien Perzen de belangrijkste Arabische wiskundigen waren.
Ontstaan van de algebra[bewerken | brontekst bewerken]

Mohammed ibn Mūsā al-Ḵwārizmī, een Perzisch wiskundige en astronoom uit de 9e eeuw, schreef verscheidene belangrijke boeken over de Arabisch-Indische cijfers en over het oplossen van vergelijkingen. Zijn boek over het rekenen met Indiase cijfers, geschreven rond 825, samen met het werk van de Arabische wiskundige Al-Kindi, waren een belangrijke factor in de verspreiding van de Indiase wiskunde en Indiase cijfers naar het westen. Het belang van Al-Khwarizmi is tot op vandaag duidelijk. Het woord algoritme bijvoorbeeld is afgeleid van de gelatiniseerde versie van zijn naam, Algoritmi, en het woord algebra is afgeleid van de titel van zijn boek: Al-Kitāb al-mukhtaṣar fī hīsāb al-ğabr wa’l-muqābala (een beknopt boek over het rekenen). Het is niet voor niets dat Al-Khwarizmi de vader van de algebra wordt genoemd. Hij heeft zowel oude algebraïsche methodes bewaard en verder uitgewerkt, maar ook vele nieuwe bijdragen geleverd aan het onderdeel.
Verdere ontwikkelingen in de algebra werden door Abu Bakr al-Karaji (953 - 1029) gemaakt in zijn traktaat al-Fakhri. Daarin legt hij machtsverheffen en worteltrekken uit. In de 10e eeuw vertaalde Abul Wafa het werk van Diophantus naar het Arabisch en definieerde hij de tangens.
Volledige inductie en integreren[bewerken | brontekst bewerken]
Het eerste wiskundige bewijs, dat gebruikmaakt van de methode van de volledige inductie dateert uit het jaar 1000, in een boek dat werd geschreven door Al-Karaji. Hij gebruikte het om wat later het binomium van Newton heette, aan te tonen. Ook rekende hij aan de driehoek van Pascal en gebruikte hij faculteiten. De Franse wiskundige historicus F. Woepcke prees Al-Karaji als "de eerste die de theorie van algebraïsch rekenen introduceerde".[41]
Abu Ali al-Hasan ibn al-Haytham was de eerste wiskundige die een formule opstelde voor de som van vierde machten, gebruikmakend van volledige inductie. Hij ontwikkelde een methode om een algemene formule op te stellen voor de som van integralen, wat een fundamentele ontwikkeling in de integraalrekening vormde.
Geboorte van de analytische meetkunde[bewerken | brontekst bewerken]

Omar Khayyám was een veelzijdig Perzisch wetenschapper, dichter en schrijver. Hij schreef in 1077 het boek Discussies over de Moeilijkheden in Euclidische wiskunde. Het ging over de gebreken in de Elementen en vooral in het parallellenpostulaat. Hiermee legde hij de basis voor de analytische meetkunde en de niet-euclidische meetkunde. Hij was een van de eersten die een algemene meetkundige oplossing vond voor vierkantsvergelijkingen en hij hervormde de kalender.
De Perzische wiskundige Nasir al-Din Tusi maakte in de 13e eeuw grote vorderingen in de boldriehoeksmeting. Hij schreef ook een werk over het parallellenpostulaat van Euclides.
In de 15e eeuw slaagde Jamshīd al-Kāshī erin om tot op 16 decimalen na de komma te berekenen. Al-Kashi vond ook een algoritme voor de berekening van een willekeurige hele macht van een getal. Dit algoritme werd later nog gebruikt door Paolo Ruffini en William George Horner. Andere belangrijke Arabische wiskundigen uit die tijd waren Ibn Yahyā al-Maghribī al-Samaw'al, Abu'l-Hasan al-Uqlidisi, Thabit ibn Qurra en Abū Kāmil Shujā ibn Aslam.
Andere Arabische ontwikkelingen[bewerken | brontekst bewerken]
Verdere Arabische ontwikkelingen binnen de wiskunde omvatten een groot deel algebra en algoritmes, maar ook in de cryptografie, integraalrekening, meetkunde en goniometrie werd grote vooruitgang geboekt:
- de ontwikkeling van de boldriehoeksmeting.[42]
- de toevoeging van een decimaal punt in Arabische getallen.[42]
- de ontdekking van alle moderne goniometrische functies.[42]
- de introductie van de cryptoanalyse en de frequentieanalyse door de wiskundige Al-Kindi.[42]
- de ontwikkeling van de analytische meetkunde.[42]
- de ontwikkeling van een vroege algemene formule voor infinitesimalen[42] en integraalrekening[42] door Abu Ali al-Hasan ibn al-Haytham.
- het begin van de algebraïsche meetkunde door Omar Khayyám.[42]
- de ontwikkeling van de getaltheorie.[42]
Stagnatie en verval[bewerken | brontekst bewerken]
Tijdens de tijd van het Ottomaanse Rijk (vanaf de 15e eeuw) stagneerde de Arabische wiskunde. Een groot deel van de Arabische wereld werd veroverd door de Ottomanen: zij hingen zoals hun voorgangers de Seltsjoeken de islam aan, en gebruikten het Arabisch alfabet voor het Turks. Dit verval wordt vaak[bron?] parallel gelinkt aan de teloorgang van de Griekse wiskunde, toen de Romeinen in de 2e eeuw v.Chr. de hellenistische wereld veroverden.
Middeleeuwse wiskunde in Europa ca. 500 - 1450[bewerken | brontekst bewerken]
De wiskunde werd in het Europa van de Middeleeuwen door totaal andere problemen gedreven dan in de huidige wiskunde. Een van die drijfveren van toen was het geloof dat wiskunde informatie kon verschaffen over de orde in de natuur, omdat volgens de Bijbel God "alle dingen had geordend in maat, getal en gewicht" (Wijsheid van Salomo 11:20).[43] Wiskunde werd als een verplicht onderdeel gegeven op de Middeleeuwse universiteiten. Mede daardoor zijn in Europa grote kathedralen gebouwd.
Vroege middeleeuwen[bewerken | brontekst bewerken]

Anicius Manlius Torquatus Severinus Boethius (vaak gespeld als Boëthius), een Romeins filosoof, schrijver en politicus uit de 5e en 6e eeuw, zorgde voor een plaats voor de wiskunde in het systeem van de septem artes liberales (7 vrije kunsten). Wiskunde (uiteraard niet onder die naam) werd toen ingedeeld onder het quadrivium, een onderdeel van dat systeem dat te maken had met aantallen en verhoudingen en dus de facto wiskunde. De 4 studies die tot het quadrivium behoorden waren:
- Arithmetica: de leer van de (abstracte) getallen.
- Geometria: meetkunde.
- Astronomia: sterrenkunde.
- Musica: harmonieleer.
Boethius schreef een aantal belangrijke werken:
- De institutione arithmetica: een vrije Latijnse vertaling van het Griekse werk Introductie tot de Arithmetica van Nicomachus.
- De institutione musica: een traktaat over muziek, eveneens ontleend aan Griekse bronnen.
- Een hele serie uittreksels van de Elementen van Euclides, die hij becommentarieerde.
Zijn werken waren eerder theoretisch dan praktisch, maar vormden de basis van de studie van de wiskunde tot de herontdekking van de Griekse en Arabische wiskunde.[44]
Renaissance van de oude wiskunde[bewerken | brontekst bewerken]

In de 12e eeuw reisden vele Europese geleerden naar Spanje en Sicilië, op zoek naar wetenschappelijke werken en teksten van Arabische oorsprong. Het ging de geleerden voornamelijk om zuivere toegepaste wetenschappen, als plantkunde, natuurkunde, astronomie en wiskunde. Vooral het boek al-Jabr wa-al-Muqabilah (Arabisch: حساب الجبر و المقابلة) van Al-Chwarizmi was bijzonder in trek. Het werd daarom in 1145 vertaald naar het Latijn door Robert van Chester. Maar ook het boek de Elementen van Euclides werd vertaald, zij het dan in verschillende versies van Adelard van Bath, Herman van Karinthië en Gerard van Cremona.
Deze nieuwe bronnen zorgden voor een vernieuwing van de West-Europese wiskunde uit die tijd. Leonardo van Pisa, beter bekend als Fibonacci, schreef zelfs het eerste echte wiskundige werk in Europa sinds de tijd van Eratosthenes, waartussen een periode van meer dan 1000 jaar zat. Het werk, Liber Abaci (Het boek van de abacus), werd geschreven in 1202, maar in 1252, vlak na zijn dood, herzien. Het werk ging over algebra en de Arabische cijfers inclusief het cijfer nul.[45] Hij introduceerde hiermee dit cijferstelsel in Europa.
De Engelsman Thomas Bradwardine beweerde in de 14e eeuw dat de snelheid v rekenkundig toenam zoals de verhouding van kracht F tot weerstand R meetkundig toeneemt. Bradwardine concretiseerde dit met enkele praktische voorbeelden, omdat de logaritme om dit uit te drukken nog niet ontdekt was. Nu kunnen we zijn stelling als volgt noteren:
De analyse van Bradwardine toont aan, dat wiskundig-technische kennis werd overgenomen van Arabieren, zoals al-Kindi, en die kennis werd uitgebreid tot verschillende fysische problemen.[47]
Vroegmoderne wiskunde in Europa ca. 1450 - 1600[bewerken | brontekst bewerken]
Boekdrukkunst: wiskunde voor iedereen[bewerken | brontekst bewerken]



De boekdrukkunst liet toe om wetenschappelijke en dus ook wiskundige werken sneller en in grotere oplagen te verspreiden. Het oudste gedrukte wiskundige boek is Theoricae nova planetarum van Georg von Peuerbach uit 1472. In 1478 volgde een anoniem boek over meetkunde, namelijk Arte dell'Abbaco. Het eerste gedrukte boek over de Elementen van Euclides verscheen in Duitsland in 1482.
Beperkingen[bewerken | brontekst bewerken]
Bij het begin van Renaissance in Europa beperkte het gebruik van Romeinse cijfers de wiskunde. Om verbanden tussen gegevens te leggen werden meer woorden dan wiskundige symbolen gebruikt. Er was bijvoorbeeld geen teken voor de optelling, geen gelijkheidsteken en geen gebruik van de x als een onbekende.
Uitvinding van de decimale schrijfwijze[bewerken | brontekst bewerken]
Een algemene oplossingsmethode voor derdegraadsvergelijkingen ontstond rond 1510. Deze ontdekking wordt toegeschreven aan Scipione del Ferro, alhoewel de methode al eerder in Neurenberg was gepubliceerd door de boekdrukker Johannes Petreius in Girolamo Cardano's traktaat Ars magna. Daarin stond ook een oplossingsmethode voor vierdegraadsvergelijkingen, die werd ontdekt door Cardano's leerling Lodovico Ferrari.[48]
De vierkantswortel uit 2 trekken en dat getal uitschrijven, was moeilijk in die tijd. De Grieken wisten al dat de uitkomst geen natuurlijk getal was, noch een decimale breuk. In de 16e eeuw werd daarop het antwoord gevonden: het kommagetal of decimale getal. De getallen werden geschreven met een komma op de plaats waar de natuurlijke schrijfwijze ophield. Deze schrijfwijze werd aanvankelijk ontwikkeld door John Napier, maar later geperfectioneerd door de Vlaamse wiskundige Simon Stevin.
In 1597 publiceerde de Duitse professor Michael Maestlin een eerste inverse schatting van de 'gulden verhouding' ('golden ratio'):[49]
De latere breukvorm geeft ons het echte getal phi:
Opkomst van de goniometrie[bewerken | brontekst bewerken]
Gedreven door de eisen van de navigatiekunde en cartografie om nauwkeuriger kaarten te tekenen van grotere gebieden (niet alleen wereldkaarten, maar ook sterrenkaarten), groeide de goniometrie (ook wel trigonometrie of driehoeksmeetkunde) uit tot één der belangrijkste takken uit de wiskunde van de 16e eeuw. Regiomontanus publiceerde in 1533 de eerste gedrukte tabel met sinus- en cosinuswaarden.[50] De Duitse wiskundige en astronoom Bartholomaeus Pitiscus was de eerste die het woord trigonometrie gebruikte, namelijk voor de titel van zijn werk Trigonometria uit 1595.
Aan het einde van de 16e eeuw hebben de Duitser Regiomontanus en de Fransman François Viète de Arabisch-Indiase cijfers ingevoerd.
Uitvinding van de complexe getallen[bewerken | brontekst bewerken]
De formule van de Italiaanse wiskundigen Scipione del Ferro en Niccolò Tartaglia voor de oplossingen van een derdegraadsvergelijking plaatste de wiskundigen van de 16e eeuw voor een nieuw probleem. Wanneer zo'n vergelijking drie verschillende (reële) oplossingen heeft, komen in die formule namelijk wortels uit negatieve getallen voor en die waren in die tijd nog niet gedefinieerd. Ze kregen de naam imaginaire getallen en de gewone getallen heetten vanaf toen 'reëel'. Rafael Bombelli, de bedenker van de complexe getallen, stelde de rekenregels op. Hierbij stelde hij als axioma de genoemde eigenschap van het imaginair getal i, waarbij i volgende eigenschap bezit:[51]
Aan het einde van de 18e eeuw legden Leonhard Euler en Carl Friedrich Gauss de basis voor de getaltheorie en de complexe functietheorie.
Wiskunde in de 17e en 18e eeuw[bewerken | brontekst bewerken]
Grote ontdekkingen[bewerken | brontekst bewerken]
In 1620 stelde Henry Briggs logaritmetafels op, door handmatig 54 opeenvolgende vierkantswortels uit 10 te trekken tot 16 cijfers na de komma. Tot de opkomst van de computer hebben zijn tabellen gediend voor alle berekeningen.
Tycho Brahe, een Deens astronoom, noteerde de posities van de planeten aan de hemel. Johannes Kepler verwerkte die gegevens met hulp van de Schot John Napier, die de natuurlijke logaritmen of naar hem genoemd Neperse logaritmen onderzocht. Kepler stelde in zijn wetten van Kepler, dat de planeten bewegen in ellipsen rond de zon. De analytische meetkunde, ontwikkeld door de Fransman René Descartes, maakte het mogelijk om die elliptische banen voor te stellen in een grafiek met het Cartesisch coördinatenstelsel.
Johannes Kepler verenigde de stelling van Pythagoras en de gulden snede in zijn driehoek van Kepler en schreef:
De meetkunde heeft twee grote schatten: de ene is de stelling van Pythagoras en de andere de verdeling van een lijn in uiterste en middelste reden; de eerste kunnen we vergelijken met een hoeveelheid goud, de tweede mogen we waarlijk een kostbaar juweel noemen.
Verkenning van nieuwe wiskundige terreinen[bewerken | brontekst bewerken]
Naast het bestuderen van de hemel en de daarop toegepaste wiskunde, begonnen enkele wetenschappers het terrein van de wiskunde uit te breiden. Pierre de Fermat en Blaise Pascal legden de grondslag voor het onderzoek naar kansrekening (dat toen nog waarschijnlijkheidsrekening heette) en de regels van de combinatoriek. Pascal, een apologeet, probeerde om de pas ontdekte regels van de kansrekening te gebruiken om het leven te wijden aan de religie. Hij beweerde het volgende: "Ook al zijn de kansen klein dat we op aarde slagen in wat we doen, de beloningen in het hiernamaals zullen veel groter zijn".
Ontdekking van de differentialen en integralen[bewerken | brontekst bewerken]

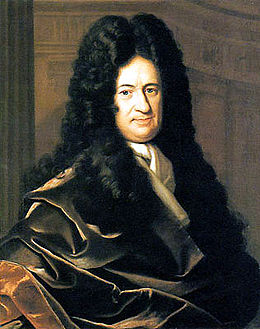
Sir Isaac Newton ontdekte zijn wetten van Newton, terwijl hij de wetten van Kepler probeerde te verklaren. Hij ontwikkelde daartoe een nieuwe wiskundige tak, de wiskundige analyse. Los van Newton ontwikkelde Gottfried Wilhelm Leibniz in Duitsland ook de analyse.
De analyse vond toepassingen van meetkundige aard (onderzoek van minima en maxima, bepaling van de raaklijn aan een kromme en de berekening van oppervlakten en inhouden) en van fysische aard (snelheid, bewegingsvergelijkingen en bewegingsvectoren), welke leidden tot nieuwe methoden, waarin het begrip oneindig een belangrijke rol speelde.
De eerste toepassingen van de integraalrekening werden gevonden op het gebied van de mechanica. Het concept van de integraal is in de loop van de tijd op allerlei manieren gegeneraliseerd en toegepast op allerlei situaties.
Leibniz voerde de notatie met de langgerekte S in. De integraal is de limiet van ; het ∫-teken is de limietvorm van het sommatieteken en stelt de integratie voor, a en b zijn de eindpunten van het interval, f(x) is de functie die geïntegreerd wordt, en dx is de limiet van Δx en stelt een infinitesimaal klein stukje van de x-as voor. Historisch gezien stelde dx een infinitesimaal voor, en de langgerekte S betekende "som". Moderne theorieën zijn hier niet meer op gebaseerd en de traditionele symbolen zijn nu alleen een wiskundige notatie. Guillaume de l'Hôpital formuleerde zijn regel van l'Hôpital in het werk L'Analyse des infiniment petits pour l'intelligence des lignes courbes (1696) voor limieten van het type 0/0 en ∞/∞.
In de 17e en 18e eeuw werden concepten als de variatierekening, gewone en partiële differentiaalvergelijkingen, Fourieranalyse en voortbrengende functies ontwikkeld voor toepassingen als onder meer diffusie van warmte. In 1697 werden vier oplossingen voor de brachistochrone kromme gepubliceerd.
Het getal e[bewerken | brontekst bewerken]
De uitvinding van de decimale schrijfwijze leidde John Napier ertoe om een nieuw constant getal te bestuderen: e, dat soms ook de constante van Napier of het getal van Euler wordt genoemd. Het kwam voor het eerst voor in een tabel in het appendix van een werk over logaritmen, van de hand van Napier, namelijk Mirifici logarithmorum canonis constructio uit 1618.[52] Toch werd het getal zelf niet genoemd, maar wel een lijst met natuurlijke logaritmen die berekend waren vanuit een constant getal. De letter e werd in 1727 door Euler, die zorgde voor een standaardisering van wiskundige termen, ingevoerd en verwijst mogelijk naar de eerste letter van het woord exponentieel. Daarvoor werd het getal aangeduid met de letters b of c.
De ontdekking van de waarde van die constante wordt toegeschreven aan Jakob Bernoulli, die erin slaagde om de volgende uitdrukking voor deze constante te vinden:
Het eerste gebruik van de constante komt voor in een brief van Gottfried Leibniz aan Christiaan Huygens in 1690 en 1691.
Euler: nieuwe wiskundige termen en symbolen[bewerken | brontekst bewerken]

door Emanuel Handmann
De Zwitser Leonhard Euler heeft de wiskundige termen gestandaardiseerd. Hij gaf rond 1777 bijvoorbeeld de vierkantswortel van −1 de naam i.[51] Hij voerde ook het gebruik van de Griekse letter in als verhouding van de omtrek van de cirkel tot zijn middellijn en gaf de naam e aan het grondtal van de natuurlijke logaritme. Ook de huidige namen van bijvoorbeeld goniometrische functies als sinus, cosinus en tangens stammen van hem. Euler bewees dat het probleem van de zeven bruggen van Koningsbergen geen oplossing bezit en legde daarmee de grondslag van de grafentheorie. Samen met Lorenzo Mascheroni ontdekte hij de constante van Euler-Mascheroni. Euler leidde de Formule van Euler af, die een "verbazend verband legt tussen e, i en , een opmerkelijke gelijkheid":[53]
als bijzonder geval van zijn meer algemene
Volgens Nobelprijswinnaar Richard Feynman is dit "de meest opmerkelijke formule van de wiskunde, ons juweel".[54]
Het Vermoeden van Goldbach[bewerken | brontekst bewerken]
Nog altijd onbewezen is het Vermoeden van Goldbach, dat Christian Goldbach formuleerde in een brief aan Leonhard Euler op 7 juni 1742:[55]
Elk even getal groter dan 2 kan geschreven worden als de som van twee priemgetallen, een priemgetal mag hierbij twee keer worden gebruikt.
Tot nu zijn getallen tot 4 × 1018 gecontroleerd en de meeste wiskundigen geloven dat het vermoeden waar is, maar er is nog geen bewijs gevonden. Grote even getallen kunnen meestal op veel manieren als de som van 2 priemgetallen worden geschreven.[56]
Wiskunde in de 19e eeuw[bewerken | brontekst bewerken]
De wiskundige analyse ontwikkelt zich verder[bewerken | brontekst bewerken]
In de 19e eeuw zorgde Augustin Louis Cauchy als eerste voor een formele basis voor de differentiaal- en integraalrekening door zijn introductie van de Cauchyrij.[57] Hij begon ook de formele theorie van de complexe analyse te ontwikkelen. Siméon Poisson, Joseph Liouville, Joseph Fourier en andere wiskundigen bestudeerden partiële differentiaalvergelijkingen en de Fourieranalyse.
In 1854 voerde Bernhard Riemann zijn integratietheorie in. De analyse kreeg enige jaren later door Weierstrass een rekenkundige in plaats van een meetkundige grondslag door zijn invoering van de ε-δ-definitie van de limiet.
Rond dezelfde tijd leidden pogingen om de integratietheorie van Riemann te verfijnen en de ontdekking van monsterlijke objecten (zoals nergens continue functies, overal continue maar nergens differentieerbare functies en ruimtevullende krommen) tot de ontwikkeling van de maattheorie door Camille Jordan.
In 1835 duikt voor het eerste de naam goldener Schnitt (gulden snede) op, in een werk van de Duitse wiskundige Martin Ohm.[58]
Gauss[bewerken | brontekst bewerken]


De 19e eeuw was de tijd van Carl Friedrich Gauss, die onderzoek verrichtte naar de complexe functietheorie, meetkunde en de convergentie van rijen. Hij gaf het eerste goede bewijs voor de hoofdstelling van de algebra en de wet van de kwadratische reciprociteit. Hij bedacht de kwadratuurformule van Gauss om integralen te benaderen en is bekend van de klok van Gauss. Hij voerde ook het modulair rekenen in voor zijn beroemde formule om de paasdatum te berekenen met de woorden notiones, non notationes, dus begrip, niet notatie is van belang.
De abstracte algebra werd gevormd door de Ierse wiskundige William Rowan Hamilton, met de ringtheorie en de quaternionen. De Brit George Boole bedacht rond 1850 een nieuwe soort algebra, die we nu kennen als de booleaanse algebra. Daarin werkt men met booleaanse operatoren + en x op de booleaanse waarden (0 en 1) en er geldt bijvoorbeeld: 1 + 1 = 1 (waar of waar = waar). Booleaanse algebra is het startpunt van de wiskundige logica en kent toepassingen in de informatica.
Ontwikkeling van de niet-euclidische meetkunde[bewerken | brontekst bewerken]
Deze eeuw zag vrijwel de hele ontwikkeling van twee nieuwe takken binnen de niet-euclidische meetkunde (namelijk de hyperbolische meetkunde en de elliptische meetkunde), waarbij het parallellenpostulaat van Euclides niet langer werd aangenomen. De Russische wiskundige Nikolai Ivanovich Lobachevsky en diens rivaal, de Hongaarse wiskundige János Bolyai, ontdekten en ontwikkelden rond 1830 onafhankelijk van elkaar de hyperbolische meetkunde, waarin de uniekheid van evenwijdige rechten niet langer stand hield. Vanaf dat moment beschouwde men twee krommen ook parallel. In deze nieuwe vorm van meetkunde kon het zijn dat de som van de hoeken van een driehoek minder of meer was dan 180° (bijvoorbeeld bij ruimtehoeken).
De elliptische meetkunde werd later in de 19e eeuw ontwikkeld door de Duitser Bernhard Riemann. Hierbij werd gesteld dat geen enkele parallelle lijn of kromme bestond en dat de som van de hoeken van een driehoek meer dan 180° was. Riemann stond ook in voor de ontwikkeling van de naar hem genoemde Riemann-meetkunde, waarin de drie typen meetkunde werden verenigd en waarbij hij het concept van variëteit definieerde. Hij werkte daarmee ook een algemeen idee uit over krommen en oppervlaktes.
Die niet-euclidische meetkunde heeft toepassingen binnen de gekromde ruimte volgens de algemene relativiteitstheorie van Albert Einstein.
Onoplosbare vraagstukken[bewerken | brontekst bewerken]
Niels Henrik Abel, een Noors wiskundige, bewees in 1824 dat er geen algemene oplossingsmethode bestaat voor een vijfdegraadsvergelijking. Andere wiskundigen uit die tijd gebruikten dit bewijs om aan te tonen dat het onmogelijk was om met een liniaal en een passer een hoek in drie gelijke delen te verdelen (het zogenaamde probleem van de trisectie).
Carl Louis Ferdinand von Lindemann toonde in 1882 aan dat het getal transcendent is. Hieruit volgt dat het niet mogelijk is om een vierkant zo te construeren dat het dezelfde oppervlakte bezit als die van een gegeven cirkel (de kwadratuur van de cirkel).
Hiermee was de onmogelijkheid bewezen om twee vraagstukken waarmee Griekse wiskundigen zich al bezighielden op te lossen.
Abels en Évariste Galois' onderzoek naar oplossingen voor vijfdegraadsvergelijkingen legden de grondslag voor de ontwikkeling van de groepentheorie en de daarmee verwante takken binnen de abstracte algebra. In de 20e eeuw vonden fysici de groepentheorie ideaal om symmetrie te bestuderen[59] in de kristalkunde en kwantumfysica.
Einde van de 19e eeuw[bewerken | brontekst bewerken]

In 1891 gaf de Duitse wiskundige Georg Cantor zijn beroemde diagonaalbewijs, waaruit blijkt dat er weliswaar even veel rationale getallen zijn als natuurlijke getallen, maar dat het aantal reële getallen groter is. Hij voerde de begrippen transfiniet getal en de kardinaal- en ordinaalgetallen in. Richard Dedekind baseerde met een nieuwe definitie door Dedekindsneden van de irrationale getallen de rekenkunde op een verzameling axioma's.
Eind 19e eeuw legde Gottlob Frege de fundamenten van de moderne, wiskundige logica en de analytische filosofie. Giuseppe Peano ten slotte werkte verder aan de formele beschrijving van de rekenkunde.
De 19e eeuw kende niet alleen een groot aantal revolutionaire ontdekkingen, maar ook een groot aantal nationale wiskundige genootschappen: de London Mathematical Society uit 1865, de Société Mathématique de France uit 1872, de Edinburgh Mathematical Society uit 1883, de Circolo Matematico di Palermo uit 1884 en de American Mathematical Society uit 1888.
Wiskunde in de 20e eeuw[bewerken | brontekst bewerken]
Voor de 20e eeuw kwamen de meeste wiskundigen uit een welgestelde familie (zoals Napier) of werden ze gestimuleerd en betaald door mecenassen (zoals Gauss). Een klein aantal, waaronder Fourier, werden betaald door colleges te geven in universiteiten. Heel wat wiskundigen, zoals Niels Henrik Abel, stierven in armoede door ziekte en verwaarlozing. Wiskunde werd in de 20e eeuw een beroep. Ieder jaar werden prijzen aan wiskundigen toegekend en er werden arbeidsplaatsen gecreëerd in onderwijs en industrie.
De 23 problemen van Hilbert[bewerken | brontekst bewerken]

In 1900 hield de Duitse wiskundige David Hilbert een lezing[60] op het Internationaal Wiskundecongres, waarop hij 23 problemen opsomde, die in de wiskunde nog onopgelost waren. Hij daagde de wiskunde uit, om ze voor het jaar 2000 allemaal op te lossen. In het jaar 2000 werd een stand van zaken opgemaakt en er bleek dat er amper 10 waren opgelost. Van de 13 overige problemen waren er nog 11 gedeeltelijk opgelost en 2 bleven open:
- Geef een bewijs van de Riemann-hypothese.
- Kan de natuurkunde uitgaande van axioma's worden beschreven?
Vandaag de dag zijn er 18 problemen opgelost, sommige door onoplosbaarheid ervan te bewijzen, 3 problemen zijn gedeeltelijk opgelost en 2 (zie hierboven) staan nog altijd open.
Srinivasa Ramanujan: autodidact en wiskundige[bewerken | brontekst bewerken]
Een van de opvallendste figuren op het wiskundige toneel in de 20e eeuw was de Indiër Srinivasa Aaiyangar Ramanujan, die, ondanks dat hij autodidact was, ongeveer 4000 stellingen bewezen of nagelaten heeft, waaronder de mogelijkheden van een hogelijk samengesteld getal, een aantal stellingen in verband met de getaltheorie en zijn beroemde Ramanujan-functie met toepassingen in de snaartheorie. Hij deed ook ontdekkingen op vlak van de gammafunctie, modulair rekenen, divergente rijen, hypergeometrische rijen en de priemgetalstelling.[61]
De wiskunde in één systeem[bewerken | brontekst bewerken]
Begin 20e eeuw werden pogingen ondernomen om de wiskunde in één enkel formeel systeem te vangen. Om te beginnen werd de rekenkunde van de natuurlijke getallen geformaliseerd. De meest geslaagde poging hiertoe werd ondernomen door Bertrand Russell en Alfred North Whitehead in hun boek Principia Mathematica.
Bewijzen van onbewijsbaarheid[bewerken | brontekst bewerken]
In 1929 bewees Kurt Gödel zijn volledigheidsstelling: de standaardpredicatenlogica was volledig. Een jaar later publiceerde hij zijn twee onvolledigheidsstellingen in een artikel in het Monatshefte für Mathematik und Physik, getiteld "Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I". De I duidt erop dat Gödel van plan was een toegankelijker vervolgartikel te schrijven, omdat hij vreesde dat zijn artikel zelfs voor zijn collega's te moeilijk zou zijn. Die vrees bleek ongegrond: het belang van zijn resultaat werd al spoedig onderkend.
De eerste stelling luidt:
Ieder axiomatisch wiskundig systeem dat voldoende krachtig is om alle basiseigenschappen van de natuurlijke getallen te bewijzen, is ofwel onvolledig (dat wil zeggen dat er ware uitspraken zijn die niet bewezen kunnen worden), ofwel inconsistent (dat wil zeggen dat er onware uitspraken zijn die wel bewezen kunnen worden).
Anders geformuleerd zal ieder consistent axiomatisch systeem van voldoende kracht om de getaltheorie in uit te drukken, stellingen kennen, die noch bewezen, noch ontkracht kunnen worden binnen dat systeem, en dus onbeslisbaar zijn.
Gödels tweede onvolledigheidsstelling houdt in dat de formele rekenkunde haar eigen consistentie niet kan bewijzen. Dat wil zeggen dat het niet kan bewezen worden binnen een gegeven consistent axiomatisch systeem.
Computerwiskunde[bewerken | brontekst bewerken]

Met de computers kwam ook de numerieke wiskunde op, een deelgebied van de wiskunde waarin algoritmes voor problemen in de analyse en differentiaalrekening bestudeerd worden. Bijvoorbeeld met de Fast Fourier transform voor analyse van golfverschijselen zoals geluid en elektromagnetische straling, en gecompliceerde wiskundige modellen, zoals eindige-elementenmethode konden worden gebouwd en doorberekend. Hiermee werd het toepassingsgebied van de wiskunde verbreed naar bijvoorbeeld weersvoorspelling en kansrekening. In de Tweede Wereldoorlog ontstonden ook toepassingen van het simplexalgoritme en Monte-Carlosimulatie en de cryptografie.
In 1976 baarden Wolfgang Haken en Kenneth Appel opzien door met een computer de vierkleurenstelling te bewijzen.
Met een supercomputer berekenden de Japanner Yasumasa Kanada en zijn team aan de Universiteit van Tokio in oktober 2005 1,241 biljoen decimalen van .[62]
Oude problemen opgelost[bewerken | brontekst bewerken]

Kurt Gödel in 1940 en Paul Cohen in het begin van de jaren 60, bewezen dat de continuümhypothese onafhankelijk is van de standaardaxioma's uit de verzamelingenleer.[63]
Aleksander Gelfond en Alan Baker bewezen de transcendentie van een groot aantal getallen onder meer de constante van Gelfond, maar van een aantal zoals de constante van Euler-Mascheroni is nog niet geweten[64] of ze transcendent of algebraïsch zijn.
In 1995 bewees Andrew Wiles de laatste stelling van Fermat. Zeven jaar lang heeft Wiles in isolement gewerkt aan dit bewijs en in 1993 presenteerde hij het resultaat voor een zaal vol wiskundigen aan het Isaac Newton Instituut in Cambridge. Bij controle onder regie van het tijdschrift Inventiones Mathematicae bleek in de bewijsvoering een fout te zitten. Samen met Richard Taylor kon Wiles het bewijs corrigeren en op 19 september 1994 was het bewijs geleverd. Het meer dan 100 pagina's tellende bewijs werd gepubliceerd in de Annals of Mathematics in mei 1995.[65] Naast de Wolfskehl-geldprijs, die in 1908 was uitgeloofd voor degene die de stelling zou bewijzen, ontving Wiles de Rolf Schock-prijs van de Koninklijke Academie van Wetenschappen van Zweden (Zweeds: Kungliga Vetenskapsakademien) in Stockholm en de Prix Fermat van de Université Paul Sabatier. Daarnaast kreeg hij in 1998 een speciale vermelding bij de uitreiking van de Fields-medaille, hoewel hij toen al boven de leeftijdsgrens van 40 jaar zat.
Wiskunde op grote schaal[bewerken | brontekst bewerken]
Wiskunde werd stilaan een wereldtaal, waardoor grotere samenwerkingsverbanden tussen allerlei universiteiten, genootschappen en instituten ontstonden. Het beroemdste voorbeeld vindt men in de groepentheorie, namelijk de classificatie van eindige enkelvoudige groepen (ook wel de "enorme stelling" genoemd). Dit project werd gehouden tussen 1955 en 1983 en het betrok meer dan 100 wiskundigen, die samen tienduizenden pagina's beschreven hebben.
Een groep Franse wiskundigen, die publiceerden onder het pseudoniem Nicolas Bourbaki, probeerden om alle kennis van de wiskunde te bundelen. Het resultaat was een gigantische hoeveelheid pagina's, gebundeld in 8 boeken, die een controversiële invloed uitoefenden op het wiskundeonderricht.[66]
Door die mondiale samenwerking ontstonden ook vele nieuwe takken van de wiskunde: wiskundige logica, topologie, complexiteitstheorie, de snaartheorie en de speltheorie.
John Conway breidde het getalbegrip uit tot de surreële getallen, die alle bekende getallen logisch definiëren en uitbreiden en formele bewijzen opleveren voor stellingen als 1 + 1 = 2.
Benoît Mandelbrot, Wacław Sierpiński, Helge von Koch en anderen ontwikkelden de theorie van de fractalen, die onder meer sponsen, waterlopen en andere fenomenen modelleert[67] met dimensies die niet langer een natuurlijk getal als 1, 2 of 3 zijn, maar een reëel getal.
Aspecten van de wiskunde[bewerken | brontekst bewerken]
Externe link[bewerken | brontekst bewerken]
- MacTutor History of Mathematics Archive van de St Andrews-universiteit: overzicht van biografieën en onderwerpen uit de geschiedenis van de wiskunde.
| Dit artikel is op 13 april 2009 in deze versie opgenomen in de etalage. |

















